This document is the third volume in the three volume set of User’s Manuals for the Micromechanics Analysis Code with Generalized Method of Cells Version 4.0 (MAC/GMC 4.0). Volume 1 is the Theory Manual, Volume 2 is the Keywords Manual, and this document is the Example Problems Manual.

MAC/GMC 4.0 is composite material and laminate analysis software developed at the NASA Glenn Research Center. It is based on the generalized method of cells (GMC) micromechanics theory (Paley and Aboudi, 1992), which provides access to the local stress and strain fields in the composite material. This access grants GMC the ability to accommodate arbitrary local models for inelastic material behavior and various types of damage and failure. The MAC/GMC 4.0 software package has been built around GMC to provide the theory with a user-friendly framework, along with a library of local inelastic, damage, and failure models. Further, application of simulated thermo-mechanical loading, generation of output results, and selection of architectures to represent the composite material, have been automated in MAC/GMC 4.0. Finally, classical lamination theory has been implemented within MAC/GMC 4.0 wherein GMC is used to model the composite material response of each ply. Thus, the full range of GMC composite material capabilities is available for analysis of arbitrary laminate configurations as well. Although the focus of previous versions of MAC/GMC has been on metallic based composites (due to the need for inelastic constitutive models for the metallic matrix), the code is fully capable of analyzing polymeric and ceramic based composites as well.

The many new features incorporated within version 4.0 of the MAC/GMC software are enumerated in the MAC/GMC 4.0 Keywords Manual Introduction. The two most important new features, from the standpoint of analysis capabilities are: 1) the ability to model electromagnetic (“smart”) composites and laminates, and 2) the incorporation of the new high-fidelity generalized method of cells (HFGMC) micromechanics theory. Electromagnetic materials and structures are those that are capable of responding electrically or magnetically to imposed thermo-mechanical loads and responding mechanically to imposed electrical or magnetic loads. These so-called “smart” materials have potential to enable the next generation of multi-functional structures that can automatically sense and react to various stimuli. Example Problems 7b and 7c illustrate the usage of the MAC/GMC 4.0 electromagnetic capabilities. The HFGMC micromechanics theory involves a formulation that enables the micromechanics model to be significantly more accurate in its predicted local stress and strain fields compared to GMC. Because this improved accuracy naturally places additional computation demands on the MAC/GMC 4.0 code, the code may now be considered to have variable fidelity. When computational efficiency is at a premium, the standard GMC micromechanics capabilities can be employed. Conversely, when local filed accuracy is more important, the HFGMC micromechanics capabilities can be employed. Example Problem 3f presents the usage of the HFGMC capabilities of MAC/GMC 4.0.

Format of this Manual

It is the objective of this manual to illustrate, through example, how to use the MAC/GMC 4.0 software. Forty-three individual example problems are presented that describe the usage of most of the code’s capabilities. The manual is broken into seven sections. The first section presents four basic examples that outline the fundamental procedures used to execute MAC/GMC 4.0 simulations. For new users of MAC/GMC, the first step towards learning to use the code should be gaining a good understanding of these basic examples. Section 7 deals with advanced topics. Sections 2 – 6 contain examples that highlight particular capabilities of the code.

The execution of MAC/GMC 4.0 is controlled by an ASCII input file that contains a number of keywords and specifiers. The keywords can be broken into groups that are related to particular capabilities of the code. The MAC/GMC 4.0 Keywords are listed with their associated groups and applicable example problems in Table I.1. These twenty-two keywords control all aspects of the MAC/GMC 4.0 execution. Each is described in detail in the MAC/GMC 4.0 Keywords Manual. The examples presented in Sections 2 – 6 in this MAC/GMC 4.0 Example Problems Manual illustrate capabilities that correspond to the keyword groups 2 – 6 given in Table I.1.

Table I.1 MAC/GMC 4.0 keywords and their associated example problems. The problems that specifically highlight a particular keyword are hyperlinked (typed in blue and underlined).

1) Flag-Type Keywords
*CHECK	None
*CONDUCTIVITY	Example 1a
*ELECTROMAG	Examples 7b, 7c
2) Material Keywords
*MDBPATH	Example 2h
*CONSTITUENTS	All example problems (required keyword) Section 2 Examples
3) Analysis Type and Architecture Keywords
*RUC	Examples 1a, 1c, 1d, 2a-h, 3a, 3b, 3c, 3d, 3e, 3f, 4a-c, 4f, 4h, 5a, 5b, 5d-f, 6a-c, 7a, 7b, 7d
*LAMINATE	Examples 1b, 3g, 3h, 3i, 4d, 4e, 4g, 5c, 5d, 6c, 7c
4) Loading Keywords
*MECH	Examples 1c, 1d, 2a-h, 3a-i, 4a, 4b, 4c, 4d, 4e, 4h, 5b-f, 6a, 6b, 7a-c
*THERM	Examples 1d, 2e-h, 3a, 3b, 3d-i, 4a, 4b-f, 4h, 5b-f, 6a-c, 7a-c
*SOLVER	Examples 1c, 1d, 2a, 2b, 2c-h, 3a-e, 3f-i, 4a, 4b-f, 4h, 5b-f, 6a-c, 7a-c
*SURF	Examples 4f, 4g
5) Damage and Failure Keywords
*ALLOWABLES	Examples 5a, 5b
*FAILURE_SUBCELL	Examples 5b, 5c, 5d
*FAILURE_CELL	Examples 5c, 5d
*DAMAGE	Example 5d
*DEBOND	Examples 5e, 5f
*CURTIN	Example 5f
6) Results and Data Output Keywords
*PRINT	All example problems
*XYPLOT	Examples 1c, 1d, 2a-h, 3a-i, 4a-d, 4h, 5b, 5d-f, 6a-c, 7a-c
*PATRAN	Example 6b
*MATLAB	Examples 3f, 6c
7) End of File Keyword
*END	All example problems (required keyword)

Each example problem presented in this manual is associated with a MAC/GMC 4.0 example problem input file (all of which are distributed with the MAC/GMC 4.0 software). A general description is given for each example problem, followed by a listing of the input file for that example problem. An “Annotated Input Data” section is given for each example problem that describes the meaning and purpose of each line of data within the input file. Finally, the results of the example problems are presented and discussed. The user should be able to reproduce these results using the provided MAC/GMC 4.0 example problem input files, upon successful installation of the software package.

This Example Problem Manual is heavily cross-referenced to the MAC/GMC 4.0 Keywords Manual (which gives an in-depth description of each keyword) and the MAC/GMC 4.0 Theory Manual (which presents the mathematical models upon which the MAC/GMC 4.0 code is based). Throughout the Example Problem Manual, when the annotated input data associated with a particular keyword is given, a cross-reference to the Section # in the MAC/GMC 4.0 Keywords Manual is given as: “[KM_#]”.

Section 1 : Basic Examples

In this first section, four basic MAC/GMC 4.0 example problems are presented that introduce many of the fundamental concepts associated with the code. Examples that appear in the subsequent sections of this manual rely on the user’s knowledge and understanding of these basic concepts, and they also borrow from the basic problem configurations represented by these four examples. The first two example problems do not involve applied loading as the code is used only to determine effective properties for a composite and a laminate. The subsequent two problems involve application of mechanical and thermal loading on a monolithic metallic alloy and a composite in which the same alloy serves as the matrix material.

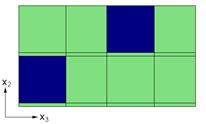
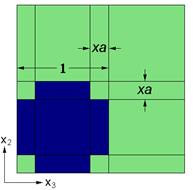
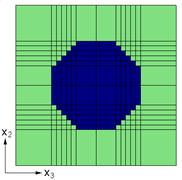
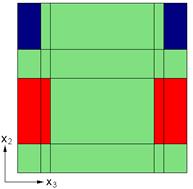
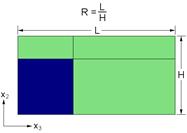
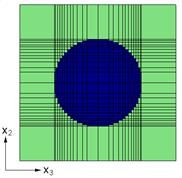
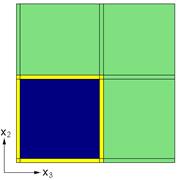
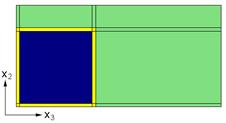
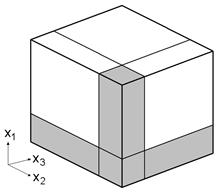
Example 1a: Effective Properties of a Composite

This example problem determines the effective thermal and mechanical properties of a continuous graphite fiber/epoxy matrix composite material. The simplest repeating unit cell (RUC) available within MAC/GMC 4.0 that can represent the architecture of this composite, namely a 2´2 RUC (see Figure 1.1), is employed. As Figure 1.1 shows, the doubly periodic RUC consists of four subcells in the x₂-x₃ plane, one of which represents the fiber and three of which represent the matrix. The term “doubly periodic” indicates that the RUC repeats infinitely in the two in-plane (x₂-x₃) directions and is infinite in the out-of-plane (continuously reinforced, x₁) direction. The RUC thus represents a continuum (as opposed to a structure with boundaries). Based on the properties and arrangement of the fiber and matrix constituents, MAC/GMC 4.0 uses the doubly periodic generalized method of cells (GMC) theory to homogenize the composite material and determine the effective (anisotropic) properties of this continuously reinforced homogenized material. The constituent material properties in this problem are temperature-independent and are read from the MAC/GMC input file.

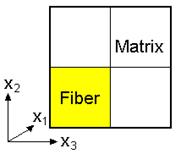
Figure 1.1 MAC/GMC 4.0 2´2 doubly periodic repeating unit cell.

MAC/GMC Input File: example_1a.mac

MAC/GMC 4.0 Example 1a - graphite/epoxy effective properties

*CONDUCTIVITY

NTEMP=1 TEMP=21.

*CONSTITUENTS

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1 &

EL=388.2E9,7.6E9,0.41,0.45,14.9E9,-0.68E-6,9.74E-6

K=500.,10.

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1 &

EL=3.45E9,3.45E9,0.35,0.35,1.278E9,45.E-6,45E-6

K=0.19,0.19

*RUC

MOD=2 ARCHID=1 VF=0.65 F=1 M=2

*PRINT

NPL=-1

*END

F Note: The lines of the input file starting with the “#” character are comments and thus ignored by the code.

Annotated Input Data

1) Flags:

a) Determine effective thermal conductivity properties (*CONDUCTIVITY) [KM_1]:

NTEMP=1 TEMP=21.

Number of conductivity temps: 1 (NTEMP=1)

Conductivity temps: 21. (TEMP=21.)

*CONDUCTIVITY is a flag-type keyword that indicates to MAC/GMC 4.0 that effective thermal conductivities should be calculated. The thermal conductivity calculation can be performed at any desired temperature (specified by NTEMP= and TEMP=). This feature is useful when the constituent properties (specified under *CONSTITUENTS) are temperature-dependent. In this example problem, the material properties are temperature-independent, so even if additional conductivity temperatures were specified, the calculated effective thermal conductivities would be the same for each temperature. Note that, in the presence of the *CONDUCTIVITY keyword, thermal conductivities for the constituent materials must be specified under *CONSTITUENTS.

2) Constituent materials (*CONSTITUENTS) [KM_2]:

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1 &

EL=388.2E9,7.6E9,0.41,0.45,14.9E9,-0.68E-6,9.74E-6

K=500.,10.

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1 &

EL=3.45E9,3.45E9,0.35,0.35,1.278E9,45.E-6,45.E-6

K=0.19,0.19

Number of materials: 2 (NMATS=2)

Constitutive models: Elastic (CMOD=6)

Materials: User-defined (Graphite) (MATID=U)

User-defined (Epoxy) (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 1.1 (EL=… and K=…)

Table 1.1 Constituent material properties for example 1a.

E_A (GPa)

E_T (GPa)

n_A

n_T

G_A (GPa)

a_A

(10^-6/ °C)

a_T

(10^-6/ °C)

k_A (W/mK)

k_T (W/mK)

Graphite

388.2

7.6

0.41

0.45

14.9

-0.68

9.74

500.

10.

Epoxy

3.45

0.35

1.278

45.

0.19

This example problem employs user-defined material properties. In the present case of elastic material constitutive behavior (as specified by CMOD=6), the temperature-independent elastic properties and coefficients of thermal expansion (CTEs) are simply listed as EL=E_A, E_T, n_A, n_T, G_A, a_A, a_T (axial and transverse elastic modulus, axial and transverse Poisson ratio, axial shear modulus, and axial and transverse CTE, respectively). The temperature-independent thermal conductivities are specified on a separate line as K=k_A, k_T (axial and transverse thermal conductivity, respectively). Note that, while the K=… specification is required when the *CONDUCTIVITY keyword is present, in the absence of *CONDUCTIVITY, K=… should be omitted. In addition, the employed elastic constitutive model (CMOD=6) allows for transversely isotropic material properties. That is, it allows for specification of different properties in the axial and transverse direction (as specified for the graphite fiber, for example). Care should be exercised, however, as CMOD=6 requires that the axial direction be associated with the x₁-axis (see Figure 1.1). For transversely isotropic elastic constituent behavior with axes other than the x₁-axis, constitutive model 9 (CMOD=9) can be employed (see Keywords Manual Section 2). The isotropic simplification of the employed elastic model (CMOD=6) is obtained by setting E_A = E_T = E, n_A = n_T = n, G_A = E/2(1+n) = G, a_A = a_T = a, and k_A = k_T.

In addition to direct specification of the constituent material properties within the MAC/GMC 4.0 input file, several other options exist for material property specification. These are: material properties taken from the code’s internal database, material properties read from an external database, and material properties determined from the user-defined subroutine (usrfun.F90). Also, for different constitutive models (specified by CMOD=), and for temperature-dependent properties, the input requirements are different. These options and requirements are described in Section 2 of the MAC/GMC 4.0 Keywords Manual, and example problems involving these options and requirements are presented in Section 2 of this Example Problem Manual.

The units of the material properties employed by MAC/GMC 4.0 are arbitrary. However, the units must be consistent in order for the MAC/GMC 4.0 results to be meaningful. It is the user’s responsibility to ensure that the constituent material property units are consistent. This is particularly important when employing constituent materials from the internal material property database. For more information on constitutive material property units, see the MAC/GMC 4.0 Keywords Manual Section 2.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

MOD=2 ARCHID=1 VF=0.65 F=1 M=2

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: square fiber, square pack (ARCHID=1)

Fiber volume fraction: 0.65 (VF=0.65)

Material assignment: graphite fiber (F=1)

epoxy matrix (M=2)

By including *RUC within the input file, repeating unit cell analysis, which represents a continuum has been selected. In this example, a repeating unit cell architecture is selected from the MAC/GMC internal library by specifying ARCHID=1. This RUC, which is the simplest representation of a continuous fiber composite, is shown in Figure 1.1. The additional information required for this RUC architecture is the fiber volume fraction and which of the two constituent materials occupy the subcells associated with the fiber (F=) and the matrix (M=). Based on the specified fiber volume fraction, MAC/GMC 4.0 determines the dimensions of each subcell. Then, given the information on which materials occupy which subcells, the code has obtained all of the data (the constituent properties and their arrangement) required to homogenize the composite and determine its effective properties via the generalized method of cells theory.

F Note: While only VF=, F=, and M= are required for ARCHID=1, other RUC architectures contained within the MAC/GMC 4.0 RUC architecture library require unique input data. Example problems dealing with other RUC architectures are presented within Section 3 of this Example Manual. For additional information on RUC architectures, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading: None

As stated earlier, this example problem involves determining effective properties only. Therefore, no simulated thermal or mechanical loading need be specified. See Example Problem 1c for an introduction on specifying applied loading histories.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

NPL=-1

Print level: -1 (effective properties only) (NPL=-1)

The print level generally indicates how much information will be written to the output file. A level of 0 prints the least amount of information while a level of 10 prints the most. In addition, a special case of NPL=-1 indicates that the code should execute only to determine effective properties (as opposed to determining the response to simulated applied loading). See the MAC/GMC 4.0 Keywords Manual Section 6 for details on the various print levels.

F Note: If NPL≠-1 at least one of the keywords *MECH and *THERM must be present in the input file.

b) x-y plots (*XYPLOT): None

Because no simulated mechanical loading is applied in the present example, no x-y plot data will be written to output files. See Example Problem 1c for an introduction to generating x-y plots.

7) End of file keyword: (*END)

The *END end of file keyword must be included in all MAC/GMC 4.0 input files.

Results

In this example problem, since MAC/GMC 4.0 is employed only to determine the effective properties of the graphite/epoxy composite, all results are contained within the output file. Recall that (as described in the Keywords Manual), if the code is executed using the command:

mac4 example_1a

then the relevant output is written to the ASCII file example_1a.out. The entirety of this output file is provided in the appendix, and the results given below were taken directly from this output file.

The results include the effective thermal conductivities of the 0.65 fiber volume fraction graphite/epoxy composite, the effective stiffness matrix (CG), the inverse of the effective compliance matrix (CI), the effective engineering moduli (i.e., effective elastic properties), and the effective coefficients of thermal expansion. Recall from Figure 1.1 that the axial fiber direction is associated with the x₁-axis, while the x₂ and x₃ directions are transverse to the continuous fiber. The high thermal conductivity, high stiffness, and low CTE associated with the axial direction of the fiber constituent are evident in the effective properties of the composite associated with the x₁ direction. Transverse to the fiber direction, on the other hand, the thermal conductivity and stiffness are low while the CTE is high.

-------------------------------------------------

Effective Thermal Conductivities

At Temperature = 21.0

K11 = 325.0665

K22 = 0.7694

K33 = 0.7694

-------------------------------------------------

--------------------- EFFECTIVE PROPERTIES AT TEMPERATURE = 21.00 ----------------------------

CG - Effective/Macro Stiffness Matrix

0.2571E+12 0.4500E+10 0.4500E+10

0.4500E+10 0.7828E+10 0.3707E+10

0.4500E+10 0.3707E+10 0.7828E+10

0.1916E+10

0.4166E+10

CI - Effective/Macro Compliance Matrix

0.3944E-11 -0.1539E-11 -0.1539E-11

-0.1539E-11 0.1653E-09 -0.7738E-10

-0.1539E-11 -0.7738E-10 0.1653E-09

0.5219E-09

0.2400E-09

Effective Engineering Moduli

E11S= 0.2535E+12

N12S= 0.3901

E22S= 0.6050E+10

N23S= 0.4682

E33S= 0.6050E+10

G23S= 0.1916E+10

G13S= 0.4166E+10

G12S= 0.4166E+10

Effective Thermal Expansion Coefficients

-0.4724E-06 0.2663E-04 0.2663E-04

------------------------------------------------------------------------------------------------

Example 1b: Effective Properties of a Laminate

This example problem, like Example 1a, involves only determination of effective properties rather than determination of the response to an applied loading history. This problem, however, involves a cross-ply [90°/0°]_s graphite/epoxy laminate rather than a unidirectional graphite/epoxy composite. Since the constituent materials are the same, the difference between the input files in this and the previous example problem amounts to replacing the *RUC keyword with the *LAMINATE keyword. While the *RUC keyword specified analysis of a continuum in Example 1a, in the present example the *LAMINATE keyword specifies analysis of the laminated plate structure (as modeled using lamination theory).

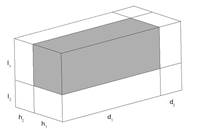
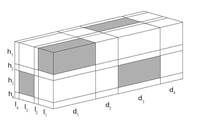
The geometry and coordinate system employed in the code for the laminate is shown in Figure 1.2. The global x-y-z coordinate system is applicable to the laminate as a whole, while the local coordinates (x₁-x₂-x₃) apply within each layer. As shown, locally, each layer is modeled using a GMC RUC analysis.

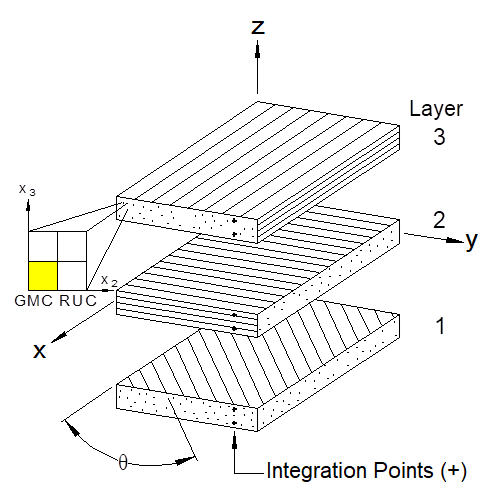
Figure 1.2 General laminate geometry and coordinate system employed in MAC/GMC 4.0. The local behavior of each layer is modeled using a generalized method of cells (GMC) repeating unit cell (RUC) analysis.

MAC/GMC Input File: example_1b.mac

MAC/GMC 4.0 Example 1b - graphite/epoxy laminate

*CONSTITUENTS

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1 &

EL=388.2E9,7.6E9,0.41,0.45,14.9E9,-0.68E-6,9.74E-6

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1 &

EL=3.45E9,3.45E9,0.35,0.35,1.278E9,45.E-6,45E-6

*LAMINATE

NLY=3

LY=1 MOD=2 THK=0.25 ANG=90 ARCHID=1 VF=0.65 F=1 M=2

LY=2 MOD=2 THK=0.50 ANG=0 ARCHID=1 VF=0.65 F=1 M=2

LY=3 MOD=2 THK=0.25 ANG=90 ARCHID=1 VF=0.65 F=1 M=2

*PRINT

NPL=-1

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Constitutive models: Elastic (CMOD=6)

Materials: User-defined (Graphite) (MATID=U)

User-defined (Epoxy) (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 1.1 (EL=… and K=…)

This example problem employs the same user-defined material properties as in Example 1a.

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

NLY=3

LY=1 MOD=2 THK=0.25 ANG=90 ARCHID=1 VF=0.65 F=1 M=2

LY=2 MOD=2 THK=0.50 ANG=0 ARCHID=1 VF=0.65 F=1 M=2

LY=3 MOD=2 THK=0.25 ANG=90 ARCHID=1 VF=0.65 F=1 M=2

Number of layers: 3 (NLY=3)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Volume fraction	Fiber material	Matrix material
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(VF)	(F)	(M)
1	GMC-2D	0.25	90°	square fiber, square pack	0.65	graphite	epoxy
2	GMC-2D	0.50	0°	square fiber, square pack	0.65	graphite	epoxy
3	GMC-2D	0.25	90°	square fiber, square pack	0.65	graphite	epoxy

Because the local behavior of each layer is represented by a GMC repeating unit cell, information similar to that specified under *RUC (in Example 1a) is now specified for each layer. Here, each layer is represented as the same unidirectional graphite/epoxy composite whose effective properties were determined in Example 1a. In addition, for each layer, the thickness (THK) and angle (ANG) in degrees must be specified. The thicknesses of the layers is important not only to provide the dimensions of the layers with respect to each other, but also to provide the overall thickness of the laminate. This overall thickness is important to the calculation of the laminate force and moment resultants during simulated applied loading. The angle specifies the orientation of each layer’s local coordinate system relative to the laminate (global coordinate system). Note that the middle layer’s thickness is twice that of the outer layers, resulting in a layup equivalent to four equal thickness layers.

Example problems dealing with other laminate configurations are presented within Section 3 of this Example Manual. For additional information on the code’s laminate analysis capabilities, see the MAC/GMC 4.0 Keywords Manual Section 3 and the MAC/GMC 4.0 Theory Manual Section 3.

4) Loading: None

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

NPL=-1

Print level: -1 (effective properties only) (NPL=-1)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

As in Example problem 1a, the results of this example are contained solely within the output file because only effective properties (as opposed to the response to applied loading) are determined. The lines below are taken directly from the output file. From the GMC repeating unit cell analysis of each layer, the effective stiffness matrix (CG), the effective compliance matrix (CI), the effective engineering moduli, and the effective CTEs are output (in local coordinates). Then, from the lamination theory analysis, the laminate axial stiffness (A), coupling stiffness (B), and bending stiffness (D) matrices are determined, as are the effective laminate engineering constants. Examining these results, it is clear that (in the local coordinates of each layer) the effective properties of each layer are identical to each other and the unidirectional composite results from Example 1a. The laminate results show that, for this symmetric cross-ply laminate, there is no coupling between extension and bending (B matrix is zero) and the laminate normal and shear behavior is decoupled (A₁₆, A₂₆, D₁₆, and D₂₆ are close to zero). Finally, the effective (apparent) elastic moduli of the laminate in the x and y directions are identical as expected.

--------------------- EFFECTIVE PROPERTIES AT TEMPERATURE = 21.00 ----------------------------

* FOR LAYER NUMBER 1 *

CG - Effective/Macro Stiffness Matrix

0.2571E+12 0.4500E+10 0.4500E+10

0.4500E+10 0.7828E+10 0.3707E+10

0.4500E+10 0.3707E+10 0.7828E+10

0.1916E+10

0.4166E+10

CI - Effective/Macro Compliance Matrix

0.3944E-11 -0.1539E-11 -0.1539E-11

-0.1539E-11 0.1653E-09 -0.7738E-10

-0.1539E-11 -0.7738E-10 0.1653E-09

0.5219E-09

0.2400E-09

Effective Engineering Moduli

E11S= 0.2535E+12

N12S= 0.3901

E22S= 0.6050E+10

N23S= 0.4682

E33S= 0.6050E+10

G23S= 0.1916E+10

G13S= 0.4166E+10

G12S= 0.4166E+10

Effective Thermal Expansion Coefficients

-0.4724E-06 0.2663E-04 0.2663E-04

--------------------- EFFECTIVE PROPERTIES AT TEMPERATURE = 21.00 ----------------------------

* FOR LAYER NUMBER 2 *

CG - Effective/Macro Stiffness Matrix

0.2571E+12 0.4500E+10 0.4500E+10

0.4500E+10 0.7828E+10 0.3707E+10

0.4500E+10 0.3707E+10 0.7828E+10

0.1916E+10

0.4166E+10

CI - Effective/Macro Compliance Matrix

0.3944E-11 -0.1539E-11 -0.1539E-11

-0.1539E-11 0.1653E-09 -0.7738E-10

-0.1539E-11 -0.7738E-10 0.1653E-09

0.5219E-09

0.2400E-09

Effective Engineering Moduli

E11S= 0.2535E+12

N12S= 0.3901

E22S= 0.6050E+10

N23S= 0.4682

E33S= 0.6050E+10

G23S= 0.1916E+10

G13S= 0.4166E+10

G12S= 0.4166E+10

Effective Thermal Expansion Coefficients

-0.4724E-06 0.2663E-04 0.2663E-04

--------------------- EFFECTIVE PROPERTIES AT TEMPERATURE = 21.00 ----------------------------

* FOR LAYER NUMBER 3 *

CG - Effective/Macro Stiffness Matrix

0.2571E+12 0.4500E+10 0.4500E+10

0.4500E+10 0.7828E+10 0.3707E+10

0.4500E+10 0.3707E+10 0.7828E+10

0.1916E+10

0.4166E+10

CI - Effective/Macro Compliance Matrix

0.3944E-11 -0.1539E-11 -0.1539E-11

-0.1539E-11 0.1653E-09 -0.7738E-10

-0.1539E-11 -0.7738E-10 0.1653E-09

0.5219E-09

0.2400E-09

Effective Engineering Moduli

E11S= 0.2535E+12

N12S= 0.3901

E22S= 0.6050E+10

N23S= 0.4682

E33S= 0.6050E+10

G23S= 0.1916E+10

G13S= 0.4166E+10

G12S= 0.4166E+10

Effective Thermal Expansion Coefficients

-0.4724E-06 0.2663E-04 0.2663E-04

----------------------- LAMINATE RESULTS AT TEMPERATURE = 21.00 -------------------------------

Laminate Axial Stiffness Matrix [A]

1.303E+11 2.369E+09 -4.748E-01

2.369E+09 1.303E+11 -2.500E+01

-4.748E-01 -2.500E+01 4.166E+09

Laminate Coupling Stiffness Matrix [B]

0.000E+00 0.000E+00 0.000E+00

Laminate Bending Stiffness Matrix [D]

3.093E+09 1.974E+08 -6.924E-02

1.974E+08 1.862E+10 -3.646E+00

-6.924E-02 -3.646E+00 3.472E+08

Laminate Engineering Constants (only valid for symmetric laminates)

Exx= 1.302E+11

Nxy= 1.819E-02

Eyy= 1.302E+11

Gxy= 4.166E+09

Example 1c: Tensile Response of Monolithic Ti-21S

This example problem demonstrates MAC/GMC’s capability to apply a loading history to a material and determine the response. For the sake of simplicity, the analyzed material is not a composite, but rather simply a monolithic titanium alloy commonly used in metal matrix composites; Ti-21S. Unlike the previous examples, the material properties for the Ti-21S are taken from the code’s internal material property database. An applied strain of 0.02 (i.e., 2%) is applied to the alloy over 200 seconds (sec.), resulting in an applied strain rate of 10^-4/sec. This example illustrates the basic form of a MAC/GMC 4.0 input file involving applied mechanical loading and also could be of interest when the response of a particular constituent material is desired.

MAC/GMC Input File: example_1c.mac

MAC/GMC 4.0 Example 1c - monolithic Ti-21S

*CONSTITUENTS

NMATS=1

M=1 CMOD=4 TREF=23. MATID=A

# M=1 CMOD=4 TREF=650. MATID=A

*RUC

MOD=1 M=1

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=1

NAME=example_1c X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

NMATS=1

M=1 CMOD=4 TREF=23. MATID=A

# M=1 CMOD=4 TREF=650. MATID=A

Number of materials: 1 (NMATS=1)

Constitutive model: Isotropic GVIPS (CMOD=4)

Material: Ti-21S (MATID=A)

Reference Temperature: 23. °C (TREF=23.)

The reference temperature for a particular constituent material indicates the temperature at which the code should evaluate the material properties for that material. This overrides the temperature-dependence of a material’s properties and causes the code to use the temperature indicated by TREF no matter what temperature the simulation is at. TREF is also useful, as in the current example, when no thermal loading is included in the simulation. In this case, without TREF, the code would not know at what temperature to take the Ti-21S material properties (and an error would result) since the properties stored for Ti-21S in the internal material database vary with temperature. Note that the temperature units (°C) are dictated by those used in the internal material database, which are always °C.

In addition, the example input file contains the line:

# M=1 CMOD=4 TREF=650. MATID=A

Here, the “#” sign in the first column indicates that this line is a “comment”, i.e., it is ignored by the code when the input file is read. Thus, by uncommenting this line and commenting out the line above, it is possible to execute the exact same case using Ti-21S material properties at 650 °C rather than 23 °C. Results for both of these temperatures are given below.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

MOD=1 M=1

Analysis model: Monolithic material (MOD=1)

Material assignment: Ti-21S (M=1)

By including *RUC within the input file, repeating unit cell analysis, which represents a continuum has been selected. In this example, a monolithic material is analyzed, and the material to be analyzed must be selected from the materials indicated in *CONSTITUENTS.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitudes: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

The loading option indicates the direction of the applied mechanical loading (see the MAC/GMC 4.0 Keyword Manual Section 4 for details on the loading options). In this case the mechanical loading is applied in the x₁-direction, with all other stress components kept at zero. The mechanical loading profile is specified through time-magnitude pairs that specify the loading history to be applied (the first time must always be zero). In MAC/GMC 4.0, the unit of time is seconds (sec.). Finally, the loading mode indicates whether strains (MODE=1) or stresses (MODE=2) are applied. The applied mechanical load history for this problem is plotted in Figure 1.3.

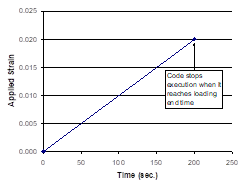
Figure 1.3 Example 1c: Applied strain vs. time history.

F Note: The applied global strain rate is 0.02 ÷ 200. sec. = 1´10^-4/sec.

b) Thermal (*THERM): None

No thermal loading is applied in this example. This necessitates the use of TREF in *CONSTITUENTS to indicate the temperature at which the material properties are taken. If a thermal loading profile were specified, TREF would not be needed (although it could be specified).

c) Time integration (*SOLVER) [KM_4]:

METHOD=1 NPT=2 TI=0.,200. STP=1.

Time integration method: Forward Euler (METHOD=1)

Number of time points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step size (from 0. – 200. sec.): 1. sec. (STP=1.)

Two explicit methods of time integration are available in MAC/GMC 4.0; Forward Euler (METHOD=1) with a specified time step and Predictor/Corrector (METHOD=2) with a self-adaptive time step size. In this example, the simpler Forward Euler method is employed. The forward Euler time integration is specified by a time point – time step size profile. Since the time step size pertains to a time segment between two time points, there will always be one fewer time step size specified than the number of time points specified. As in *MECH, the first time must always be zero.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

NPL=6

Print level: 6 (NPL=6)

The print level indicates how much information will be written to the output file. A level of 0 prints the least amount of information while a level of 10 prints the most. A print level of 6 results in an intermediate level of writing to the output file including the effective stiffness matrix at each time step. See the MAC/GMC 4.0 Keyword Manual Section 6 for details on the various print levels.

b) x-y plots (*XYPLOT) [KM_6]:

FREQ=5

MACRO=1

NAME=example_1c X=1 Y=7

MICRO=0

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot name: example_1c (NAME=example_1c)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

In this example, a macro (repeating unit cell level) plot file containing the σ₁₁-ε₁₁ stress-strain response is generated as indicated by the macro plot x-y quantities X=1, Y=7 (see the MAC/GMC 4.0 Keyword Manual Section 6 for details on the macro plot x-y quantities). No micro (subcell level) plots are generated. The frequency indicates how often data will be written to the x-y plot data file. In this case, data will be written every 5 time steps (and thus every 5 seconds of the simulated applied loading). The extension “_macro.data” is appended to the indicated macro plot file name, so, in this example, the file “EXAMPLE_1c_macro.data” is written to the path location associated with the input file.

7) End of file keyword: (*END)

Results

Results are written to both the output file and the x-y plot file in this example. The output file contains all input information regarding the case executed, as well as calculated effective properties and detailed information at each time step in the loading profile (depending on the print level indicated in *PRINT). It is a good idea to check the output file for warnings, which can indicate a problem or unintended result of the input data specified. In the present example, the code has generated two warnings based on the use of TREF and the lack of thermal loading information. The data written to the x-y plot file have been plotted in Figure 1.4. Clearly, the Ti-21S stress-strain response exhibits a significant effect of temperature. Given temperature dependent material properties, MAC/GMC 4.0 captures the temperature dependence in the results, whether for a monolithic material (as in the present case) of for a composite (see Example 1d).

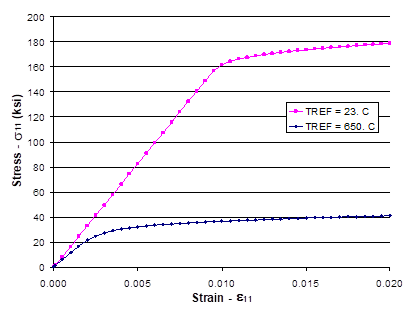
Figure 1.4 Example 1c: plot of the simulated σ₁₁-ε₁₁ stress-strain response of Ti-21S at 23. °C and 650 °C. Note that the 650 °C results were generated by commenting and uncommenting the appropriate lines in the input file under *CONSTITUENTS. Note that the global applied strain rate in this example is 1´10^-4/sec.

Example 1d: Tensile/Thermal Response of SiC/Ti-21S

This problem demonstrates several MAC/GMC simulations for a metal matrix composite. The composite is 0.25 fiber volume fraction unidirectional SiC/Ti-21S, and it has been represented with the 2´2 doubly periodic GMC repeating unit cell shown in Figure 1.1. One subcell represents the SiC fiber while the remaining three subcells are associated with the Ti-21S matrix. The material properties for both constituents are taken from the internal material database. Several applied loading cases are considered in this example. By commenting and uncommenting lines under *MECH and *THERM, results are generated for the longitudinal and transverse tensile response of the composite at both 23 °C and 650 °C.

MAC/GMC Input File: example_1d.mac

MAC/GMC 4.0 Example 1d - SiC/Ti-21S mechanical & thermal loading

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=1 VF=0.25 F=1 M=2

*MECH

LOP=1

# LOP=2

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=23.,23.

# NPT=2 TI=0.,200. TEMP=650.,650.

# NPT=2 TI=0.,200. TEMP=23.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=4

NAME=example_1d_11 X=1 Y=7

NAME=example_1d_22 X=2 Y=8

NAME=example_1d_11t X=100 Y=1

NAME=example_1d_22t X=100 Y=2

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

F Note: In contrast to example 1c, TREF is not included in the constituent data for this example. Thus, the temperature dependent material property data within the MAC/GMC 4.0 internal material database are employed – the code determines the material properties at the current temperature during the simulation. The temperature history is specified under *THERM.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: square fiber, square pack (ARCHID=1)

Fiber volume fraction: 0.25 (VF=0.25)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

In this case, a repeating unit cell (RUC) architecture is selected from the MAC/GMC 4.0 internal library. Further, it is specified which materials from *CONSTITUENTS occupy the subcell associated with the fiber and the subcells associated with the matrix in the chosen RUC (see Figure 1.1).

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 or 2 (LOP=1 or LOP=2)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitudes: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

Included is the line:

# LOP=2

By uncommenting this line and commenting the line above (LOP=1), the loading option can be switched to apply loading in the transverse (x₂) direction rather than the longitudinal (x₁) direction. As before, in directions other than that of the applied loading, the appropriate stress components are kept at zero.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 23., 23.; 650., 650.; (TEMP=23.,23., TEMP=650.,650., or

23., 650. TEMP=23.,650.)

Much as the applied mechanical loading profile is specified with time-magnitude pairs in *MECH, the applied thermal loading profile is specified with time-temperature pairs in *THERM. Included are the lines:

NPT=2 TI=0.,200. TEMP=23.,23.

# NPT=2 TI=0.,200. TEMP=650.,650.

# NPT=2 TI=0.,200. TEMP=23.,650.

By uncommenting the second line and commenting the first line, the simulation will occur at a temperature of 650 °C rather than 23 °C. For the case of applied pure thermal loading, the first two lines are commented while the third line is uncommented. This causes the code to apply a simulated heat-up from 23 °C to 650 °C. In addition, to eliminate the simulated applied mechanical loading for this case, the entirety of the *MECH section must be commented. Thus, for the pure thermal loading case, the *MECH – *THERM section of the input file should appear as:

#*MECH

# LOP=1

# LOP=2

# NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

# NPT=2 TI=0.,200. TEMP=23.,23.

# NPT=2 TI=0.,200. TEMP=650.,650.

NPT=2 TI=0.,200. TEMP=23.,650.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step size: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 4 (MACRO=4)

Macro plot names: example_1d_11 (NAME=example_1d_11)

example_1d_22 (NAME=example_1d_22)

example_1d_11t (NAME=example_1d_11t)

example_1d_22t (NAME=example_1d_22t)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

ε₂₂, σ₂₂ (X=2 Y=8)

temperature, ε₁₁ (X=100 Y=1)

temperature, ε₂₂ (X=100 Y=2)

Number of micro plots: 0 (MICRO=0)

In this example, four macro (repeating unit cell level) x-y plot files are generated, one for the σ₁₁-ε₁₁ stress-strain response, one for the σ₂₂-ε₂₂ stress-strain response, one for the temperature-ε₁₁ response, and one for the temperature-ε₂₂ response. For the case of longitudinal applied loading (LOP=1) and the thermal loading case, the σ₂₂ values written to the x-y plot file will all be zero. Similarly, for the case of transverse applied loading (LOP=2) and the thermal loading case, the σ₁₁ values written to the x-y plot file will all be zero.

7) End of file keyword: (*END)

Results

Figure 1.5 presents plots of the composite response to the applied global longitudinal (along fiber the fiber direction) and transverse (perpendicular to the fiber direction) (see Figure 1.1) strain loading at both 23 °C and 650 °C. The right hand side of the plot represents the stress-strain response in the direction of the applied loading, while the left hand side of the plot shows the strain response normal to the loading direction (i.e., the Poisson effect). These results show that the composite is significantly stiffer in the longitudinal fiber direction compared to the direction transverse to the fibers. When the loading is applied transverse to the fiber direction, the resulting Poisson effect strain is small due to the presence of the continuous fibers normal to the loading direction. At elevated temperature, the composite is much softer and exhibits more inelastic deformation than at room temperature. Figure 1.6, which is a plot of the composite’s longitudinal and transverse thermal response to a globally stress free heat up, shows that the composite exhibits greater strain during the thermal loading in the transverse direction compared to the longitudinal direction.

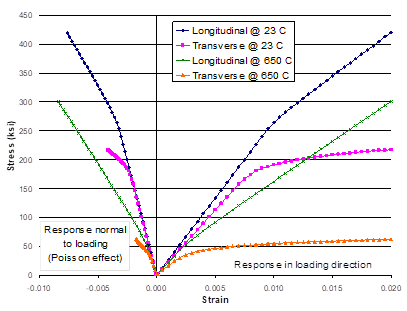
Figure 1.5 Example 1d: plot of the simulated longitudinal (along the fiber direction) and transverse (perpendicular to the fiber direction) stress-strain response of a 25% SiC/Ti-21S composite at 23. °C and 650 °C. The strain response normal to the loading direction (i.e., Poisson effect) is also plotted.

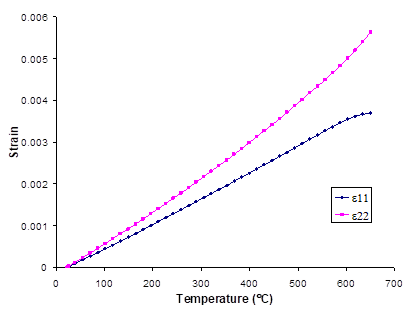
Figure 1.6 Example 1d: plot of the simulated longitudinal and transverse temperature-strain response of a 25% SiC/Ti-21S.

Section 2 : Constituent Materials

This section presents example problems intended to illustrate MAC/GMC’s capabilities with respect to constituent materials. Constituent materials are the building blocks of the composite materials that the code is designed to analyze. Constituent materials occupy the individual subcells that constitute the repeating unit cell used by the micromechanics models to represent the composite. An important concept related to constituent materials is that of a constitutive model. By definition, associated with each constituent material is a constitutive model. The constitutive model is what determines the reaction of the material to the stresses and strains experienced by the material during a MAC/GMC simulation. Then, based on the reaction of the constituent materials in each subcell, the micromechanics model determines the reaction of the composite as a whole.

The basic form of the material constitutive equation employed in MAC/GMC 4.0 can be written,

where is the stress vector, is the material stiffness matrix, is the strain vector, is the inelastic strain vector, and is the thermal strain vector. The function of the constitutive model is essentially, given (or ) for the material at point, to determine (or ) at that point. Thus, the constitutive model for a material must include information on the stiffness matrix of the material (), as well as the inelastic and thermal strains ( and ). Note that MAC/GMC employs this engineering notation wherein the stress and strain tensors are reduced to vectors. The ordering of the components within these vectors is: s = (s₁₁, s₂₂, s₃₃, s₂₃, s₁₃, s₁₂) and ε = (ε ₁₁, ε ₂₂, ε ₃₃, γ₂₃, γ₁₃, γ₁₂), where γ_ij are the engineering shear strain components.

The stiffness matrix and thermal strains within the constitutive equation written above are fairly straight forward. The elastic properties of the material determine the stiffness matrix, while the material coefficient of thermal expansion (CTE), in conjunction with the temperature history, determines the thermal strains. For a linearly elastic material, this is all that is required from the constitutive model. For a material that undergoes inelastic deformation, like the Ti-21S material employed in Example Problems 1c and 1d, the constitutive model must also determine the inelastic strains. This is usually much more complex as inelastic strains typically exhibit history/time/rate dependence, which demands a great deal from the constitutive model, particularly for metals.

MAC/GMC 4.0 includes an internal database of constituent materials, each of which is associated with a particular constitutive model. In Example Problem 1d, two internal database materials, each associated with a different constitutive model, were employed. The Ti-21S matrix material was associated with the isotropic GVIPS viscoplastic constitutive model, while the SiC fiber material was associated with the linearly elastic constitutive model. In Example Problems 1a and 1b, although user-defined material properties were specified for the graphite and epoxy constituent materials, the internal linear elastic constitutive model (CMOD=6) was employed for both materials. Section 2 of this manual presents example problems involving many of the other constituent materials and constitutive models contained within MAC/GMC 4.0. The code also includes the ability for users to employ their own material properties with an internal constitutive model. Further, users may also implement their own material constitutive model through MAC/GMC’s user-defined subroutines. Finally, the users may employ MAC/GMC’s external material database to store and keep track of their material parameters using a simple ASCII interface.

Example 2a: Bodner-Partom Viscoplastic Constitutive Model

This example problem generates the room-temperature tensile stress-strain response of the monolithic constituent materials within the MAC/GMC 4.0 internal material database that are associated with the Bodner-Partom viscoplastic constitutive model. The input file is similar to that employed in Example 1c, with changes associated with the constituent materials. As in Example 1c, this problem examines the response of monolithic inelastic materials and employs an applied strain rate of 10^-4/sec.

MAC/GMC Input File: example_2a.mac

MAC/GMC 4.0 Example 2a - Bodner-Partom Viscoplastic Constitutive Model

*CONSTITUENTS

NMATS=7

# -- Al 2024-T4

M=1 CMOD=1 TREF=23. MATID=A

# -- Al 2024-0

M=2 CMOD=1 TREF=23. MATID=B

# -- Al 6061-0 (a)

M=3 CMOD=1 TREF=23. MATID=C

# -- Al 6061-0 (b)

M=4 CMOD=1 TREF=23. MATID=D

# -- Al pure

M=5 CMOD=1 TREF=23. MATID=E

# -- Ti pure

M=6 CMOD=1 TREF=23. MATID=F

# -- Cu

M=7 CMOD=1 TREF=23. MATID=G

*RUC

MOD=1 M=1

# MOD=1 M=2

# MOD=1 M=3

# MOD=1 M=4

# MOD=1 M=5

# MOD=1 M=6

# MOD=1 M=7

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=0.025

*PRINT

NPL=6

*XYPLOT

FREQ=10

MACRO=1

NAME=example_2a X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 7 (NMATS=7)

Constitutive model: Bodner-Partom (CMOD=1)

Materials: Al 2024-T4, Al 2024-0, (MATID=A-G)

Al 6061-0 (a), Al 6061-0 (b),

Al pure, Ti pure, Cu

Reference Temperature: 23. °C (TREF=23.)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: Each constituent successively (M=1-7)

F Note: Each material in *CONSTITUENTS is assigned to the monolithic material successively by commenting and uncommenting the appropriate lines for separate executions of the code.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitudes: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM): None

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step size: 0.025 sec. (STP=0.025)

F Note: A very small time step size is employed in this example (0.025 sec.) compared to that used in Examples 1c and 1d, which employed the isotropic GVIPS constitutive model (1. sec.). The smaller time step required for convergence of the forward Euler integration scheme is due to the numerically stiff nature of the Bodner-Partom model equations. A smaller time step is directly associated with increased execution time, thus, in many cases it is preferable to employ the alternative time integration method, the predictor-corrector (METHOD=2) when utilizing the Bodner-Partom model as this integration scheme allows for a variable time step. See Example 4h, which employs this predictor-corrector method, for more information.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 0 (NPL=0)

F Note: A print level of 0 results in minimal output being written to the output file.

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 10 (FREQ=10)

Number of macro plots: 1 (MACRO=1)

Macro plot name: example_2a (NAME=example_2a)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

This example problem illustrates how MAC/GMC 4.0 can be used to quickly generate the response of the materials within the internal material database. By altering the materials in *CONSTITUENTS, the user can use the example 2a input file to generate the response of other materials within the code’s internal material database at any temperature desired.

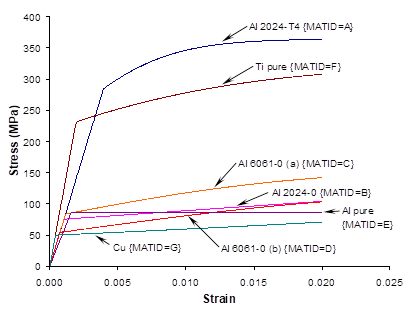
Figure 2.1 Example 2a: plots of the room-temperature tensile stress-strain response of the seven materials within the MAC/GMC 4.0 internal material database that are associated with the Bodner-Partom viscoplastic constitutive model.

Example 2b: Strain-Rate Dependence of Ti-21S

This example problem examines the elevated temperature strain rate (SR) dependence of two different constitutive models for the same material, namely Ti-21S. Ti-21S is associated with both the isotropic GVIPS viscoplastic constitutive model and the modified Bodner-Partom (MBP) viscoplastic constitutive model in the MAC/GMC 4.0 internal material database (see the Keyword Manual Section 2). Both models incorporate strain rate dependence, but, as this example shows, the elevated temperature inelastic behavior of Ti-21S predicted by each of these models is different. The applied strain rate is altered from 10^-4/sec. to 10^-5/sec. to 10^-6/sec. by commenting and uncommenting the appropriate lines under *MECH and *SOLVER.

MAC/GMC Input File: example_2b.mac

MAC/GMC 4.0 Example 2b - Strain Rate Dependence of Ti-21S

*CONSTITUENTS

NMATS=2

# -- Ti-21S Isotropic GVIPS

M=1 CMOD=4 TREF=650. MATID=A

# -- Ti-21S MBP

M=2 CMOD=2 TREF=650. MATID=A

*RUC

MOD=1 M=1

# MOD=1 M=2

*MECH

LOP=1

NPT=2 TI=0.,20. MAG=0.,0.02 MODE=1

# NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

# NPT=2 TI=0.,2000. MAG=0.,0.02 MODE=1

*SOLVER

METHOD=1 NPT=2 TI=0.,20. STP=0.0025

# METHOD=1 NPT=2 TI=0.,200. STP=0.025

# METHOD=1 NPT=2 TI=0.,2000. STP=0.25

*PRINT

NPL=0

*XYPLOT

FREQ=200

MACRO=1

NAME=example_2b X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Constitutive models: Isotropic GVIPS (CMOD=4)

Modified Bodner-Partom (CMOD=2)

Materials: Ti-21S (MATID=A)

Reference Temperature: 650. °C (TREF=650.)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: Each constituent successively (M=1,2)

Each of the two materials in *CONSTITUENTS is assigned to the monolithic material successively by commenting and uncommenting the appropriate lines.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 20. sec. (TI=0.,20.)

0., 200. sec. (TI=0.,200.)

0., 2000. sec. (TI=0.,2000.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

F Note: By altering the time points in the mechanical loading history, the global strain rate is decreased from 10^-3/sec. to 10^-4/sec. to 10^-5/sec.

b) Thermal (*THERM): None

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 2 (NPT=2)

Time points: 0., 20. sec. (TI=0.,20.)

0., 200. sec. (TI=0.,200.)

0., 2000. sec. (TI=0.,2000.)

Time step sizes: 0.0025 sec. (STP=0.0025)

0.025 sec. (STP=0.025)

0.25 sec. (STP=0.25)

As in Example 2a, the very small time step sizes employed in this example are due to the stiff nature of the modified Bodner-Partom equations. A much larger step size can be used for the GVIPS cases presented in this example.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 0 (NPL=0)

b) x-y plots (*XYPLOT):

Frequency: 200 (FREQ=200)

Number of macro plots: 1 (MACRO=1)

Macro plot name: example_2b (NAME=example_2b)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

The results for this example problem are shown in Figure 2.2. While the qualitative effect of changing the strain rate is similar for both Ti-21S constitutive models, the predicted stress-strain curves at each strain rate are somewhat different quantitatively. This demonstrates that the different constitutive models within MAC/GMC 4.0 give different results, even for the same material. For an illustration of the impact of these types of constitutive model differences, see Bednarcyk and Arnold (2002).

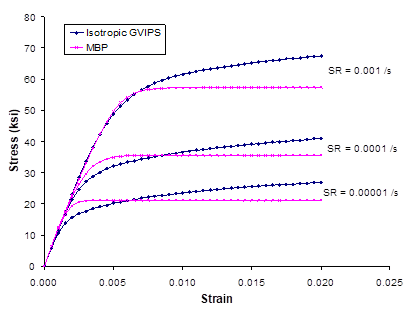
Figure 2.2 Example 2b: plots of the tensile stress-strain response of Ti-21S at 650 °C as modeled by the isotropic GVIPS and modified Bodner-Partom (MBP) constitutive models as a function of the applied strain rate (SR).

Example 2c: Incremental Plasticity

This example problem generates the room-temperature tensile response of the materials associated with the incremental plasticity constitutive model within the MAC/GMC 4.0 internal material database. Incremental plasticity represents a special case for the code in that, due to the presence of a yield surface, global iterations must occur at each increment of the applied loading in order to ensure that the plastically deforming material remains on the yield surface. Further, while the incremental plasticity constitutive model is history-dependent, the modeled inelastic behavior is independent of strain rate. The inelastic behavior of the material is defined by a yield stress and a number of stress-total strain pairs that dictate the path of the stress-strain response after yielding. These stress-total strain pairs can be obtained from experimental stress-strain curves for the material. In the simplest case, if only one post-yield stress-strain pair is specified, bilinear plasticity results. If more than one post-yield stress-strain pair is specified, point-wise plasticity results. The MAC/GMC 4.0 internal material database contains materials with bilinear incremental plasticity responses and two materials with point-wise incremental plasticity responses. This example problem considers the monolithic materials and applies strain at a rate of 10^-4/sec.

MAC/GMC Input File: example_2c.mac

MAC/GMC 4.0 Example 2c - Incremental Plasticity

*CONSTITUENTS

NMATS=4

# -- OFHC Copper - Bilinear

M=1 CMOD=21 TREF=23. MATID=A

# -- Ti-24-11 - Bilinear

M=2 CMOD=21 TREF=23. MATID=B

# -- Ti-15-3 - Point-wise

M=3 CMOD=21 TREF=23. MATID=C

# -- Ti-24-11 - Point-wise

M=4 CMOD=21 TREF=23. MATID=D

*RUC

MOD=1 M=1

# MOD=1 M=2

# MOD=1 M=3

# MOD=1 M=4

*MECH

LOP=1

NPT=2 TI=0.,20. MAG=0.,0.02 MODE=1

*SOLVER

METHOD=1 NPT=2 TI=0.,20. STP=0.1 ITMAX=20 ERR=0.0001

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=1

NAME=example_2c X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 4 (NMATS=4)

Constitutive models: Incremental plasticity (CMOD=21)

Materials: OFHC Cu – bilinear (MATID=A)

Ti-24-11 – bilinear (MATID=B)

Ti-15-3 – point-wise (MATID=C)

Ti-24-11 – point-wise (MATID=D)

Reference Temperature: 23. °C (TREF=23.)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: Each constituent successively (M=1-4)

Each of the materials in *CONSTITUENTS is assigned to the monolithic material successively by commenting and uncommenting the appropriate lines.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 20. sec. (TI=0.,20.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM): None

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 2 (NPT=2)

Time points: 0., 20. sec. (TI=0.,20.)

Time step sizes: 0.1 sec. (STP=0.1)

Max. number of iterations 20 (ITMAX=20)

Max. permitted error fraction 0.0001 (ERR=0.0001)

Due to the necessity of iteration at each time step in the simulation, two additional specifiers are required under *SOLVER when incremental plasticity is employed for a constituent material. These are the maximum number of iterations permitted at a particular time step (ITMAX) and the maximum permitted error fraction for convergence (ERR). The maximum number of iterations places a ceiling on the number of iterations at a particular time step. Once this number of iterations is reached, the code will advance to the next time step regardless of whether or not convergence has occurred (in which case a warning will be written to the output file). Generally, this non-convergent situation should be avoided by using a large value for ITMAX. The maximum permitted error fraction is the fractional change in the local effective plastic strain increment between iterations that can be considered “small enough”. That is, for example, if the largest fractional change in the effective plastic strain increment over all subcells at a particular time step is 0.00009, and ERR has been set to 0.0001, convergence is considered to have been achieved for that time step. The appropriate value for ERR is case dependent, and there is an inverse relationship between the time step size and ERR. If oscillations are present in the results, a lower value of ERR and/or a smaller time step should be employed.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot name: example_2c (NAME=example_2c)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

The results for this example problem are plotted in Figure 2.3. The difference between bilinear and point-wise representations of the material stress-strain response is clear.

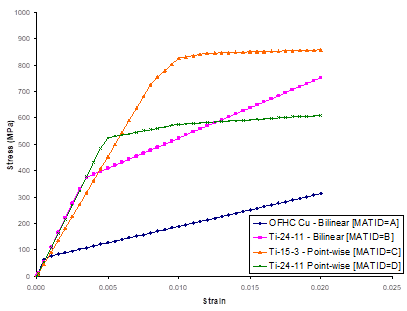
Figure 2.3 Example 2c: plots of the room-temperature tensile stress-strain response of OFHC Cu, Ti-24-11 (bilinear), Ti-15-3, and Ti-24-11 (point-wise) as modeled by the incremental plasticity constitutive model.

Example 2d: Shape Memory Alloy (SMA)

This example problem generates the tensile response of a NiTi shape memory alloy (SMA), using a specially designed constitutive model, which accounts for phase changes within the material. This model is a new capability within MAC/GMC 4.0. Cyclic strain-controlled mechanical loading is applied to the monolithic SMA at a rate of 0.001/sec.

MAC/GMC Input File: example_2d.mac

MAC/GMC 4.0 Example 2d - Shape Memory Alloy

*CONSTITUENTS

NMATS=1

M=1 CMOD=30 TREF=71.1 MATID=A

# M=1 CMOD=30 TREF=2.2 MATID=A

*RUC

MOD=1 M=1

*MECH

LOP=1

NPT=3 TI=0.,45.,90. MAG=0.,0.045,0. MODE=1,1

*SOLVER

METHOD=1 NPT=3 TI=0.,45.,90. STP=0.25,0.25

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=1

NAME=example_2d X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 1 (NMATS=1)

Constitutive models: Graesser – Cozzarelli (CMOD=30)

– Witting SMA model

Materials: NiTi SMA (MATID=A)

Reference Temperatures: 71.1. °C, 2.2 °C (TREF=71.1 or TREF=2.2)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: SMA (M=1)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 3 (NPT=3)

Time points: 0., 45., 90. sec. (TI=0.,45.,90.)

Load magnitude: 0., 0.045, 0. (MAG=0.,0.045,0.)

Loading mode: strain control (MODE=1,1)

In order to illustrate the unique features of the SMA constitutive model, a complete mechanical loading and unloading cycle has been employed.

b) Thermal (*THERM): None

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 3 (NPT=3)

Time points: 0., 45., 90. sec. (TI=0.,45.,90.)

Time step sizes: 0.25, 0.25 sec. (STP=0.25,0.25)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot name: example_2d (NAME=example_2d)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 2.4 shows that, at both temperatures, the implemented constitutive model captures the superelastic behavior of the NiTi SMA. That is, upon mechanical unloading, the SMA returns to its original shape. This “shape memory” behavior is due to stress-induced phase transformations that occur in the NiTi during loading and unloading, as modeled by the Graesser – Cozzarelli – Witting SMA constitutive model. Upon complete mechanical unloading, the stress-strain curves return to the origin, indicating that no permanent or irreversible deformation has occurred.

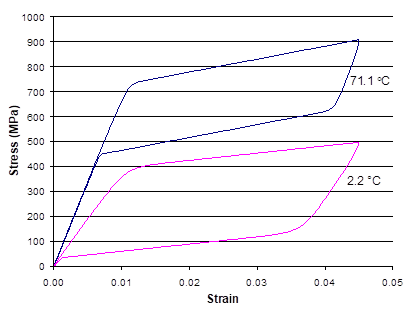
Figure 2.4 Example 2d: plots of the tensile stress-strain response of the NiTi SMA as simulated using the Graesser – Cozzarelli – Witting constitutive model at 71.1 °C and 2.2 °C.

Example 2e: User-Defined Material Properties – Input File

This example problem shows how users can specify their own constituent material properties for internal MAC/GMC 4.0 constitutive models through the code’s input file. Note that Example Problems 1a and 1b touched on this subject. The present example includes ten materials in order to illustrate the input format for the elastic, Bodner-Partom, isotropic GVIPS, and incremental plasticity constitutive models (resulting in a large input file). To switch among the materials in separate code executions, the appropriate material number is specified under *RUC. A strain rate of 10^-4/sec. is employed, and results are generated for at a temperature of 500 °C. Another way in which the user can specify constituent material properties is through the use of a user-defined subroutine, which can calculate the material properties as a function of temperature or other quantity during code execution. This type of problem is illustrated in Example 2f. In the present example, the temperature-dependent or temperature-independent material properties are typed directly into the input file. It should be noted that the input file format for user-defined material properties is slightly different for each material constitutive model (as necessitated by the different material parameters needed for each constitutive model). See Section 2 of the MAC/GMC 4.0 Keywords Manual for more information on user-defined material properties.

MAC/GMC Input File: example_2e.mac

MAC/GMC 4.0 Example 2e - User-Defined Material Properties

*CONSTITUENTS

NMATS=10

# -- Elastic; Temp-independent

M=1 CMOD=6 MATID=U MATDB=1 &

EL=58.E3,58.E3,0.20,0.20,24.17E3,6.3E-6,6.3E-6

# -- Elastic; Temp-dependent

M=2 CMOD=6 MATID=U MATDB=1

NTP=4

TEM=18.,200.,400.,600.

EA=45.6E3,43.5E3,40.6E3,29.0E3

ET=45.6E3,43.5E3,40.6E3,29.0E3

NUA=0.41,0.41,0.41,0.41

NUT=0.41,0.41,0.41,0.41

GA=16.154E3,15.429E3,14.400E3,10.286E3

ALPA=4.5E-6,4.8E-6,5.1E-6,5.5E-6

ALPT=4.5E-6,4.8E-6,5.1E-6,5.5E-6

# -- Bodner-Partom; Temp-independent

M=3 CMOD=1 MATID=U MATDB=1 &

EL=9.53E3,9.53E3,0.33,0.33,3.58E3,21.06E-6,21.06E-6 &

VI=1.E4,49.,63.,300.,4.,1.

# -- Bodner-Partom; Temp-dependent

M=4 CMOD=1 MATID=U MATDB=1

NTP=2

TEM=18.,700.

EA=9.53E3,4.12E3

ET=9.53E3,4.12E3

NUA=0.41,0.41

NUT=0.41,0.41

GA=3.58E3,1.46E3

ALPA=21.06E-6,28.92E-6

ALPT=21.06E-6,28.92E-6

V1=1.E4,1.E4

V2=49.,49.

V3=63.,63.

V4=300.,300.

V5=4.,2.5

V6=1.,1.

# -- Isotropic GVIPS; Temp-independent

M=5 CMOD=4 MATID=U MATDB=1 &

EL=14009.,14009.,0.365,0.365,5131.5,5.862E-6,5.862E-6 &

VI=0.000999275,44.960,1.679E-07,2.494561E-05,0.05, &

3.3,1.8,1.35,0.85,3.0183E-7,0.001

# -- Isotropic GVIPS; Temp-dependent

M=6 CMOD=4 MATID=U MATDB=1

NTP=6

TEM=25.,300.,482.,565.,650.,704.

EA=16.5506E+03,15.644E+03,14.009E+03,12.968E+03,11.702E+03,10.793E+03

ET=16.5506E+03,15.644E+03,14.009E+03,12.968E+03,11.702E+03,10.793E+03

NUA=0.365,0.365,0.365,0.365,0.365,0.365

NUT=0.365,0.365,0.365,0.365,0.365,0.365

GA=6062.491,5730.403,5131.502,4750.183,4286.477,3953.480

ALPA=4.2921E-06,5.116E-06,5.862E-06,6.271E-06,6.741E-06,7.07E-06

ALPT=4.2921E-06,5.116E-06,5.862E-06,6.271E-06,6.741E-06,7.07E-06

V1=99.927,20.015,0.000999275,8.499E-08,8.E-8,1.02973E-12

V2=149.964,111.965,44.960,4.786,0.8499,0.10877

V3=0.,0.,1.679E-07,1.685E-07,0.000001,0.00006

V4=9.992748E-06,1.493836E-05,2.494561E-05,7.048586E-05, &

8.498912E-05,9.224075E-05

V5=0.05,0.05,0.05,0.05,0.05,0.05

V6=3.3,3.3,3.3,3.3,3.3,3.3

V7=1.8,1.8,1.8,1.8,1.8,1.8

V8=1.35,1.35,1.35,1.35,1.35,1.35

V9=0.8498912,0.8498912,0.8498912,0.8498912,0.8498912,0.8498912

V10=1.7984E-8,3.6484E-8,3.0183E-7,3.5965E-7,1.5246E-7,1.3429E-7

V11=0.001,0,0,0,0,0

# -- Bilinear plasticity; Temp-independent

M=7 CMOD=21 MATID=U MATDB=1 &

EL=10000.,10000.,0.326,0.326,3770.,12.00E-6,12.00E-6 &

NP=1 VI=5.08,13.1,0.15

# -- Bilinear plasticity; Temp-dependent

M=8 CMOD=21 MATID=U MATDB=1

NTP=3

TEM=21.,400.,800.

EA=10000.,9000.,7300.

ET=10000.,9000.,7300.

NUA=0.326,0.351,0.345

NUT=0.326,0.351,0.345

GA=3771.,3331.,2714.

ALPA=12.00E-6,13.50E-6,22.72E-6

ALPT=12.00E-6,13.50E-6,22.72E-6

NP=1

V1=5.08,4.21,3.05

V2=13.1,10.7,5.10

V3=0.15,0.15,0.15

# -- Point-wise plasticity; Temp-independent

M=9 CMOD=21 MATID=U MATDB=1 &

EL=10000.,10000.,0.326,0.326,3770.,12.00E-6,12.00E-6 &

NP=3 VI=4.20,6.13,6.60,13.1,0.004,0.01,0.15

# -- Point-wise plasticity; Temp-dependent

M=10 CMOD=21 MATID=U MATDB=1

NTP=3

TEM=21.,400.,800.

EA=10000.,9000.,7300.

ET=10000.,9000.,7300.

NUA=0.326,0.351,0.345

NUT=0.326,0.351,0.345

GA=3771.,3331.,2714.

ALPA=12.00E-6,13.50E-6,22.72E-6

ALPT=12.00E-6,13.50E-6,22.72E-6

NP=3

V1=4.20,3.81,3.05

V2=6.13,4.77,3.69

V3=6.60,5.10,3.90

V4=13.1,9.70,5.10

V5=0.004,0.004,0.004

V6=0.01,0.01,0.01

V7=0.15,0.15,0.15

*RUC

# -- Alter value of M=* to change simulated material

MOD=1 M=1

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=500.,500.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=0.1 ITMAX=20 ERR=1.E-6

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=1

NAME=example_2e X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 10 (NMATS=10)

Materials: User-Defined (MATID=U)

Material property source: Read from input file (MATDB=1)

Constitutive models:

Linear Elastic (CMOD=6)

# -- Elastic; Temp-independent

M=1 CMOD=6 MATID=U MATDB=1 &

EL=58.E3,58.E3,0.20,0.20,24.17E3,6.3E-6,6.3E-6

# -- Elastic; Temp-dependent

M=2 CMOD=6 MATID=U MATDB=1

NTP=4

TEM=18.,200.,400.,600.

EA=45.6E3,43.5E3,40.6E3,29.0E3

ET=45.6E3,43.5E3,40.6E3,29.0E3

NUA=0.41,0.41,0.41,0.41

NUT=0.41,0.41,0.41,0.41

GA=16.154E3,15.429E3,14.400E3,10.286E3

ALPA=4.5E-6,4.8E-6,5.1E-6,5.5E-6

ALPT=4.5E-6,4.8E-6,5.1E-6,5.5E-6

The simplest constitutive model for which to input user-defined material properties is the linearly elastic model (CMOD=6). Since the material deformation is treated as linearly elastic, all that is needed is the thermo-elastic material properties. The standard order for the material properties is: . As shown above, for temperature-independent material properties, these properties are simply listed as EL=…, on the same line in the input file. For temperature-dependent material properties, the number of input temperatures (NTP=4) is placed on a separate line, followed by a separate line specifying the input temperatures (TEM=…). Then, each of the seven material properties is placed on its own separate line, with the values at each of the input temperatures listed.

Bodner-Partom (CMOD=1)

# -- Bodner-Partom; Temp-independent

M=3 CMOD=1 MATID=U MATDB=1 &

EL=9.53E3,9.53E3,0.33,0.33,3.58E3,21.06E-6,21.06E-6 &

VI=1.E4,49.,63.,300.,4.,1.

# -- Bodner-Partom; Temp-dependent

M=4 CMOD=1 MATID=U MATDB=1

NTP=2

TEM=18.,700.

EA=9.53E3,4.12E3

ET=9.53E3,4.12E3

NUA=0.41,0.41

NUT=0.41,0.41

GA=3.58E3,1.46E3

ALPA=21.06E-6,28.92E-6

ALPT=21.06E-6,28.92E-6

V1=1.E4,1.E4

V2=49.,49.

V3=63.,63.

V4=300.,300.

V5=4.,2.5

V6=1.,1.

For the Bodner-Partom viscoplastic constitutive model, the user-defined elastic material properties are specified in the same manner as for the elastic material constitutive model. Now, however, six viscoplastic material properties must also be specified. In the case of temperature-independence, these six material parameters are simply listed on the same line as the elastic properties as VI=…. In the case of temperature-dependence, each viscoplastic material property is placed on its own line as shown above. Obviously, the order in which these viscoplastic material properties is specified is important as the code must know how to interpret the input data. For the Bodner-Partom model, this order is: . This order, as well as the proper order for the other MAC/GMC 4.0 internal constitutive models, is described in Section 2 of the MAC/GMC 4.0 Keywords Manual.

Isotropic GVIPS (CMOD=4)

# -- Isotropic GVIPS; Temp-independent

M=5 CMOD=4 MATID=U MATDB=1 &

EL=14009.,14009.,0.365,0.365,5131.5,5.862E-6,5.862E-6 &

VI=0.000999275,44.960,1.679E-07,2.494561E-05,0.05, &

3.3,1.8,1.35,0.85,3.0183E-7,0.001

# -- Isotropic GVIPS; Temp-dependent

M=6 CMOD=4 MATID=U MATDB=1

NTP=6

TEM=25.,300.,482.,565.,650.,704.

EA=16.5506E+03,15.644E+03,14.009E+03,12.968E+03,11.702E+03,10.793E+03

ET=16.5506E+03,15.644E+03,14.009E+03,12.968E+03,11.702E+03,10.793E+03

NUA=0.365,0.365,0.365,0.365,0.365,0.365

NUT=0.365,0.365,0.365,0.365,0.365,0.365

GA=6062.491,5730.403,5131.502,4750.183,4286.477,3953.480

ALPA=4.2921E-06,5.116E-06,5.862E-06,6.271E-06,6.741E-06,7.07E-06

ALPT=4.2921E-06,5.116E-06,5.862E-06,6.271E-06,6.741E-06,7.07E-06

V1=99.927,20.015,0.000999275,8.499E-08,8.E-8,1.02973E-12

V2=149.964,111.965,44.960,4.786,0.8499,0.10877

V3=0.,0.,1.679E-07,1.685E-07,0.000001,0.00006

V4=9.992748E-06,1.493836E-05,2.494561E-05,7.048586E-05, &

8.498912E-05,9.224075E-05

V5=0.05,0.05,0.05,0.05,0.05,0.05

V6=3.3,3.3,3.3,3.3,3.3,3.3

V7=1.8,1.8,1.8,1.8,1.8,1.8

V8=1.35,1.35,1.35,1.35,1.35,1.35

V9=0.8498912,0.8498912,0.8498912,0.8498912,0.8498912,0.8498912

V10=1.7984E-8,3.6484E-8,3.0183E-7,3.5965E-7,1.5246E-7,1.3429E-7

V11=0.001,0,0,0,0,0

As with Bodner-Partom viscoplasticity, employing user-defined material properties with the GVIPS constitutive model requires specification of viscoplastic material properties in addition to the elastic properties. Now, instead of six viscoplastic parameters, there are eleven. As mentioned previously, the correct order for specification of these eleven properties is discussed in the MAC/GMC 4.0 Keywords Manual in Section 2.

Incremental Plasticity (CMOD=21)

# -- Bilinear plasticity; Temp-independent

M=7 CMOD=21 MATID=U MATDB=1 &

EL=10000.,10000.,0.326,0.326,3770.,12.00E-6,12.00E-6 &

NP=1 VI=5.08,13.1,0.15

# -- Bilinear plasticity; Temp-dependent

M=8 CMOD=21 MATID=U MATDB=1

NTP=3

TEM=21.,400.,800.

EA=10000.,9000.,7300.

ET=10000.,9000.,7300.

NUA=0.326,0.351,0.345

NUT=0.326,0.351,0.345

GA=3771.,3331.,2714.

ALPA=12.00E-6,13.50E-6,22.72E-6

ALPT=12.00E-6,13.50E-6,22.72E-6

NP=1

V1=5.08,4.21,3.05

V2=13.1,10.7,5.10

V3=0.15,0.15,0.15

# -- Point-wise plasticity; Temp-independent

M=9 CMOD=21 MATID=U MATDB=1 &

EL=10000.,10000.,0.326,0.326,3770.,12.00E-6,12.00E-6 &

NP=3 VI=4.20,6.13,6.60,13.1,0.004,0.01,0.15

# -- Point-wise plasticity; Temp-dependent

M=10 CMOD=21 MATID=U MATDB=1

NTP=3

TEM=21.,400.,800.

EA=10000.,9000.,7300.

ET=10000.,9000.,7300.

NUA=0.326,0.351,0.345

NUT=0.326,0.351,0.345

GA=3771.,3331.,2714.

ALPA=12.00E-6,13.50E-6,22.72E-6

ALPT=12.00E-6,13.50E-6,22.72E-6

NP=3

V1=4.20,3.81,3.05

V2=6.13,4.77,3.69

V3=6.60,5.10,3.90

V4=13.1,9.70,5.10

V5=0.004,0.004,0.004

V6=0.01,0.01,0.01

V7=0.15,0.15,0.15

The incremental plasticity constitutive model is a special case in terms of specifying user-defined material properties. The implementation of this model with MAC/GMC 4.0 allows the constituent material’s response to be defined by a number of stress – total strain point pairs that can be taken directly from experimental data for a material. Note that this simplifies the input compared to specification of stress – inelastic strain point pairs. A maximum of nine such pairs is permitted for each temperature. As shown above, the number of these stress-strain point pairs employed by the user must be specified as NP=*. This is the number of stress-strain pairs that are specified in addition to the material’s yield stress. In the case of temperature-independence, NP=* is placed on the same line, while for temperature-dependence, NP=* is placed on its own line. The smallest permitted value for NP=* is 1, which corresponds to bilinear plasticity. In this case, three plastic material parameters are specified, the first being the yield stress, followed by the stress and strain corresponding to one post-yield stress-strain pair. The material response is bilinear in that, at stresses below yield, the stress-strain response is linearly elastic, while after yielding, the response follows a linear path defined by the yield stress – total strain point and the single specified post-yield stress – total strain pair. The case where NP > 1, is referred to as point-wise plasticity, as the post-yield material response will follow a piece-wise linear path defined by the (up to nine) specified stress – total strain point pairs. The order for the user-defined properties for point-wise plasticity is:

where is the yield stress and are the stress – total strain points. As indicated above, this ordering holds true for temperature-dependent material properties as well, as each value on a particular line represents a different temperature. For instance, V1=4.20,3.81,3.05 are the values of the yield stress at the three input temperatures (21., 400., and 800. °C), V2=6.13,4.77,3.69 are the stress values () of the first stress-strain point at the three input temperatures, and V5=0.004,0.004,0.004 are the total strain values () of the first stress-strain point at the three input temperatures. Note that the total number of incremental plasticity material parameters is 2´NP+1.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: Each constituent successively (M=*)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 500., 500. (TEMP=500.,500.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 2 (NPT=2)

Time points: 0., 20. sec. (TI=0.,20.)

Time step sizes: 0.1 sec. (STP=0.1)

Max. number of iterations 20 (ITMAX=20)

Max. permitted error fraction 1.´10^-6 (ERR=1.E-6)

F Note: While ITMAX=20 and ERR=1.E-6 are present in the input file for all ten cases executed in this example problem, these data are required only for the incremental plasticity cases. As mentioned in Example 2c, if oscillations occur in the results, a smaller value for ERR and/or a smaller time step should be employed.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 1 (MACRO=1)

Macro plot name: example_2e (NAME=example_2e)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

The results for this example problem are plotted in Figure 2.5 and Figure 2.6. When temperature-dependent material properties are specified (as they are for material numbers 2, 4, 6, 8, and 10), MAC/GMC 4.0 uses linear interpolation to determine the properties at temperature between those specified. When temperature-independent material properties are specified, these properties are employed regardless of the current temperature during the simulation. Since the stress-strain results presented here were generated at a temperature of 500 °C, significant differences are evident between the temperature-dependent and temperature-independent materials for each constitutive model.

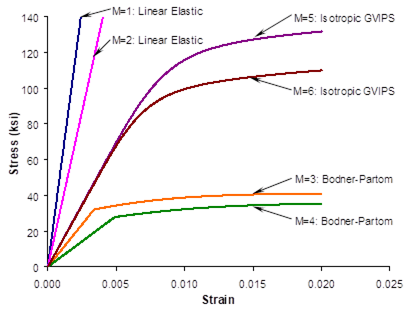
Figure 2.5 Example 2e: plots of the tensile stress-strain response of the first 6 user-defined materials at 500 °C.

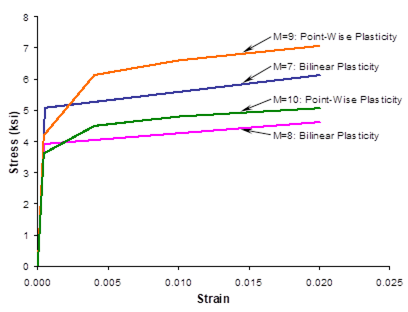
Figure 2.6 Example 2e: plots of the tensile stress-strain response of the incremental plasticity user-defined materials at 500 °C.

Example 2f: User-Defined Material Properties – USRFUN

This example problem illustrates how the user-defined subroutine, usrfun.F90, can be used in conjunction with internal MAC/GMC 4.0 constitutive models to calculate user-defined material properties during execution of the code. The usrfun.F90 subroutine used in this example is part of the MAC/GMC 4.0 executable. The usrfun.F90 source code is also distributed with the MAC/GMC 4.0 executable, along with a library file from MAC/GMC 4.0. In order for users to employ their own code to calculate material properties during code execution, it is necessary not only to include the applicable code within the usrfun.F90 source file, but also to compile the file and link it with the MAC/GMC 4.0 library file. This can be accomplished on a Windows (NT, 2000, XP) PC using the Compaq Visual Fortran software package (v. 6.6) (see http://www.compaq.com/fortran/). For additional information, see the MAC/GMC 4.0 Keywords Manual Introduction (Using User-Defined Subroutines with MAC/GMC 4.0).

It is important to note that in MAC/GMC 4.0, the material properties are associated with constituent materials as opposed to subcells. That is, several subcells may contain material #1, and thus all of those subcells must have the same material properties. This is relevant when employing the usrfun.F90 subroutine to make material properties a function of field variables, as is done in this example for materials #1 and #2. If, for instance, the properties of material #1 are determined from a function of strain and material #1 is placed in two subcells, the subcells will in general experience different strain states. It is thus impossible for material #1 to have the correct material properties to correspond to the two different states of strain in each subcell. For this reason, when material properties are determined from a function of field variables (other than temperature, which does not vary within the repeating unit cell), each subcell should be given its own material. The present example employs only one subcell, so this is not a problem in this case.

The user-editable portion of the usrfun.F90 subroutine associated with the three materials examined in this example problem is given in the Appendix. This subroutine is listed in its entirety in the Keywords Manual Appendix. The first material is elastic and has properties that are a function of the axial strain and the previous stiffness. The second material is modeled using incremental plasticity and the post-yield properties are a function of the strain rate. The third material is modeled using the Bodner-Partom viscoplastic constitutive model and the material properties are a function of temperature. The code can be executed for each of these monolithic materials by changing the material number under *RUC. The thermo-mechanical loading history can also be altered to generate the cases presented in the Results.

MAC/GMC Input File: example_2f.mac

MAC/GMC 4.0 Example 2f - USRFUN Material Properties

*CONSTITUENTS

NMATS=3

M=1 CMOD=6 MATID=U MATDB=2

M=2 CMOD=21 MATID=U MATDB=2

M=3 CMOD=1 MATID=U MATDB=2

*RUC

# -- Alter value of M=* to change simulated material

MOD=1 M=1

*MECH

LOP=1

# -- Alter values of TI=* to change simulated rate

# Example: use TI=0.,2000. for rate = 0.00001/sec.

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

# -- Alter values of TI=* to change simulated rate

# -- Alter values of TEMP=* to change simulated temperature

NPT=2 TI=0.,200. TEMP=23.,23.

*SOLVER

# -- Alter values of TI=* (and STP=*) to change simulated rate

METHOD=1 NPT=2 TI=0.,200. STP=1. ITMAX=50 ERR=1.E-6

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=1

NAME=example_2f X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 3 (NMATS=3)

Constitutive models: Linearly elastic (CMOD=6)

Incremental plasticity (CMOD=21)

Bodner-Partom viscoplasticity (CMOD=1)

Materials: User-defined (MATID=U)

Material property source: usrfun.F90 subroutine (MATDB=2)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: Each constituent successively (M=*)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

To alter the strain rate as is done to generate Figure 2.8, the second time point can be changed. For example, to increase the applied strain rate from 0.0001 /sec. to 0.001 /sec., use TI=0.,20..

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 23., 23. (TEMP=23.,23.)

F Note: The ending time point should match up with that given in *MECH. Also, to alter the temperature as is done to generate Figure 2.9, both temperature values (TEMP=*,*) should be changed.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 0.1 sec. (STP=0.1)

Max. number of iterations 50 (ITMAX=50)

Max. permitted error fraction 1.´10^-6 (ERR=1.E-6)

F Note: While ITMAX=50 and ERR=1.E-6 are present in the input file for all cases executed in this example problem, these data are required only for the incremental plasticity cases. Also, as was the case in *THERM, the ending time point must be altered to match that employed in *MECH. Also, as the total time for the simulation is altered, as in Figure 2.8, the time step size can be changed accordingly so that the total number of time steps remains constant.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 1 (MACRO=1)

Macro plot name: example_2f (NAME=example_2f)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Results in the form of simulated stress-strain curves are given in Figure 2.7, Figure 2.8, and Figure 2.9. It is important to remember that these results have been generated based on the version of the ursfun.F90 subroutine that is distributed with MAC/GMC 4.0. This version of the subroutine is contained within the distributed MAC/GMC 4.0 executable. However, if the usrfun.F90 subroutine source code is altered and compiled and linked to the MAC/GMC 4.0 library file, this example problem may not execute as expected.

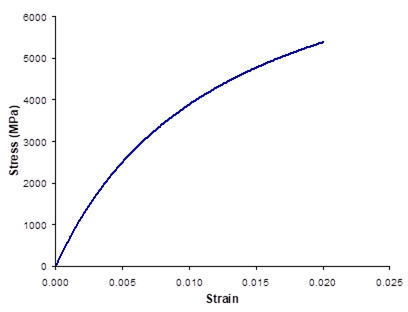
Figure 2.7 Example 2f: plot of the tensile stress-strain response for material #1 – elastic material with stiffness a function of strain and previous stiffness.

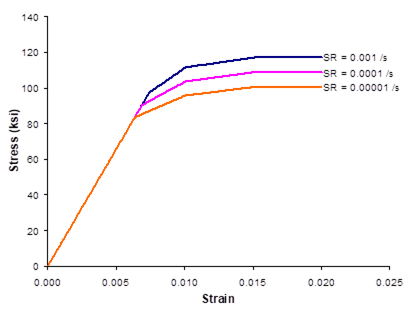
Figure 2.8 Example 2f: plots of the tensile stress-strain response for material #2 – point-wise incremental plasticity material with post-yield behavior a function of strain rate.

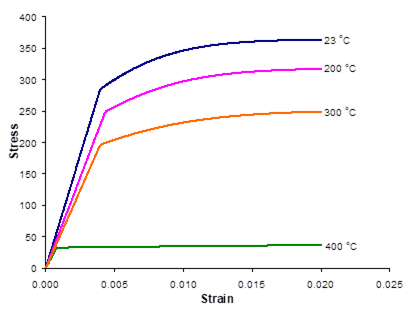
Figure 2.9 Example 2f: plots of the tensile stress-strain response for material #3 – Bodner-Partom viscoplastic material with elastic and viscoplastic material properties a function of temperature.

Example 2g: User-Defined Material Constitutive Model

This example problem illustrates how to employ the user-defined subroutine, usrmat.F90, for implementation of a user’s own constitutive model. The appropriate code that calculates the inelastic strain increments for the user’s constitutive model must be placed in the file usrmat.F90. As was the case in the previous example, this subroutine must be compiled and linked with the MAC/GMC 4.0 library file in order to be used. In this example, a power law creep model and the Bodner-Partom model have been coded within usrmat.F90. An additional user-defined subroutine must also be implemented in conjunction with the usrmat.F90 routine. This subroutine, called usrformde.F90, is employed to calculate the stiffness matrix for the user-defined material. In general, since a user-defined constitutive model can employ any elastic material parameters desired by the user, the code will not know how to determine the required stiffness matrix from the user’s elastic material parameters. Thus, the user must provide the code to do this in usrformde.F90. The user-defined portions of the usrmat.F90 and usrformde.F90 subroutines are given in the Appendix. The full listing of these subroutines is provided in the MAC/GMC 4.0 Keywords Manual Appendix.

Note that the specification of the material properties is somewhat different for a user-defined constitutive model. Particularly, the number of elastic and inelastic parameters that code should read in must be specified. The present example also includes several types of mechanical loading. In addition to the standard applied strain history, this problem involves a stress-controlled creep test simulation in which a stress is applied to the material and then held constant as the material creeps.

MAC/GMC Input File: example_2g.mac

MAC/GMC 4.0 Example 2g - USRMAT Constitutive Model

*CONSTITUENTS

NMATS=2

M=1 CMOD=99 MATID=U MATDB=1 NPE=2 NPV=2 &

EL=55.2E9,0.30 ALP=22.5E-6,22.5E-6 VI=1.5E-28,3.0

M=2 CMOD=99 MATID=U MATDB=1 NPE=2 NPV=6 &

EL=55.2E9,0.30 ALP=22.5E-6,22.5E-6 &

VI=1000.,103.42E6,103.42E6,1700.,10.,1.0

*RUC

# -- Alter value of M=* to change simulated material

MOD=1 M=1

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

# NPT=3 TI=0.,10.,3600. MAG=0.,87.2E6,87.2E6 MODE=2,2

# NPT=3 TI=0.,10.,3600. MAG=0.,80.E6,80.E6 MODE=2,2

*THERM

NPT=2 TI=0.,200. TEMP=23.,23.

# NPT=3 TI=0.,10.,3600. TEMP=23.,23.,23.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=0.05

# METHOD=1 NPT=3 TI=0.,10.,3600. STP=0.05,0.05

*PRINT

NPL=6

*XYPLOT

FREQ=20

MACRO=2

NAME=example_2g X=1 Y=7

NAME=example_2g X=101 Y=1

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

NMATS=2

M=1 CMOD=99 MATID=U MATDB=1 NPE=2 NPV=2 &

EL=55.2E9,0.30 ALP=22.5E-6,22.5E-6 VI=1.5E-28,3.0

M=2 CMOD=99 MATID=U MATDB=1 NPE=2 NPV=6 &

EL=55.2E9,0.30 ALP=22.5E-6,22.5E-6 &

VI=1000.,103.42E6,103.42E6,1700.,10.,1.0

Number of materials: 2 (NMATS=2)

Constitutive models: User-defined (CMOD=99)

Materials: User-defined (MATID=U)

Material property source: Input file (MATDB=1)

No. of Elastic Props: 2 (NPE=2)

No. of Viscoplastic Props: 2, 6 (NPV=2, NPV=6)

Since the materials employ user-defined constitutive models, the number of elastic (NPE) and viscoplastic (NPV) material parameters must be specified by the user. Then, the elastic and viscoplastic material parameters are listed as EL=… and VI=…, respectively. Temperature-dependent material parameters may be specified as well, for details, see the MAC/GMC 4.0 Keywords Manual Section 2.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: Each constituent successively (M=*)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

# NPT=3 TI=0.,10.,3600. MAG=0.,87.2E6,87.2E6 MODE=2,2

# NPT=3 TI=0.,10.,3600. MAG=0.,80.E6,80.E6 MODE=2,2

Loading option: 1 (LOP=1)

Number of points: 2 or 3 (NPT=2, NPT=3)

Time points: 0., 200. sec. (TI=0.,200.)

0., 10., 3600. sec. (TI=0.,10.,3600.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

0., 80., 80. MPa (MAG=0.,80.E6,80.E6)

0., 87.2, 87.2 MPa (MAG=0.,87.2E6,87.2E6)

Loading mode: strain control (MODE=1)

stress control (MODE=2,2)

Two types of mechanical loading are specified that can be switched by commenting and uncommenting the appropriate lines. The first line specifies mechanical loading in the form of a standard strain-controlled (MODE=1) stress-strain test. The second and third lines specify simulated stress-controlled (MODE=2) creep tests at two different stress levels. In these simulated creep tests, the load is applied quickly in stress control, and then held for 3600 sec. During this hold time, the material is free to creep.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 or 3 (NPT=2 or NPT=3)

Time points: 0., 200. sec. (TI=0.,200.)

0., 10., 3600. sec. (TI=0.,10.,3600.)

Temperature points: 23., 23. °C (TEMP=23.,23.)

23., 23., 23. °C (TEMP=23.,23.,23.)

By commenting and uncommenting the appropriate lines, the thermal time points should match those in the mechanical loading under *MECH.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 or 3 (NPT=2 or NPT=3)

Time points: 0., 200. sec. (TI=0.,200.)

0., 10., 3600. sec. (TI=0.,10.,3600.)

Time step sizes: 0.05 sec. (STP=0.05)

0.05, 0.05 sec. (STP=0.05,0.05)

Again, the appropriate lines should be commented and uncommented such that the appropriate time profile is specified for the desired case.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 20 (FREQ=20)

Number of macro plots: 2 (MACRO=2)

Macro plot names: example_2g (NAME=example_2g)

example_2g (NAME=example_2g)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

time, ε₁₁ (X=101 Y=7)

Number of micro plots: 0 (MICRO=0)

Since both macro x-y plot files are given the same name, the number 2 will be appended to the name of the second file. Thus, this input file will cause the code to write x-y plot data to the files: example_2g_macro.data and example_2g2_macro.data. See the MAC/GMC 4.0 Keywords Manuals Section 6 for details.

7) End of file keyword: (*END)

Results

Figure 2.10 shows that at an applied strain rate of 10^-4/sec., the user-defined power law creep and Bodner-Partom materials exhibit similar tensile stress-strain behavior. However, as shown in Figure 2.11, the creep behavior of the two materials is completely different at both applied stress levels. Note that because this example problem employs the versions of the user-defined subroutines (usrmat.F90 and usrformde.F90) that are distributed with MAC/GMC 4.0, this example problem cannot be expected to yield the same results if the code is calling altered version of these subroutines. Conversely, the user should ensure that the distributed versions of these subroutines are not being called when the intention is to have MAC/GMC 4.0 call the user’s own versions of these subroutines.

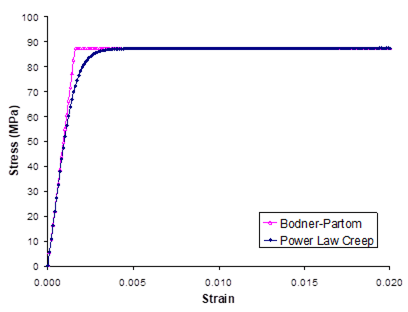
Figure 2.10 Example 2g: plot of the tensile stress-strain response for user-defined material constitutive models.

Figure 2.11 Example 2g: plot of the creep response for user-defined material constitutive models at two applied stress levels.

Example 2h: External Material Database

This example problem employs the external material database capabilities of MAC/GMC 4.0. This material database provides users with another option for storing their constituent material properties – in an external ASCII file rather than directly in the input file. Users can thus construct their own database of material properties in a single (or multiple) file(s) and access them from MAC/GMC 4.0 at will. To reference a particular external material database file from a MAC/GMC 4.0 input file, the additional keyword, *MDBPATH, is specified. It is clear from the contents of the external material database ASCII file (given below) that the format of this file is similar to that of the *CONSTITUENTS section of the input file. The main difference is that the information for each material in the external file begins with the line MAT=*, which specifies the name of the material. This name is the referenced in the input file in the *CONSTITUENTS section. The only other difference in the form of the external material database is that the line following the material name specification line specifies the constitutive model for the material (CMOD=*). The material constitutive model is also specified for each material in the input file, and the constitutive model specified in both files must match, or an error will occur. For more information on the external material database capabilities, see the MAC/GMC 4.0 Keywords Manual Section 2.

MAC/GMC Input File: example_2h.mac

MAC/GMC 4.0 Example 2h - External Material Database

*MDBPATH

NAME=sample_material_database.mat

*CONSTITUENTS

NMATS=3

M=1 CMOD=1 MATID=U MATDB=3 EXTMAT=copper

M=2 CMOD=99 MATID=U MATDB=3 EXTMAT=Al(6061-0)

M=3 CMOD=6 MATID=U MATDB=3 EXTMAT=SCS-6

*RUC

# -- Alter value of M=* to change simulated material

MOD=1 M=1

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=23.,23.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=0.02

*PRINT

NPL=6

*XYPLOT

FREQ=20

MACRO=1

NAME=example_2h X=1 Y=7

MICRO=0

*END

External Material Database File:

sample_material_database.mat

Sample Material Database Provided with MAC/GMC 4.0

# ------- Bodner-Partom Model Material

MAT=copper

CMOD=1

EL=120.E9,120.E9,0.33,0.33,45.11E9,14.7E-6,14.7E-6 &

VI=1.E4,63.E6,250.E6,8.19,7.5,0.55

# ------- Isotropic, Elastic Materials

MAT=SCS-6

CMOD=6

NTP=5

TEM=21.0,316.0,427.0,538.0,860.0

EA=393.E9,382.E9,378.E9,374.E9,368.E9

ET=393.E9,382.E9,378.E9,374.E9,368.E9

NUA=0.25,0.25,0.25,0.25,0.25

NUT=0.25,0.25,0.25,0.25,0.25

GA=157.2E9,152.8E9,151.2E9,149.6E9,147.2E9

ALPA=3.56E-6,3.73E-6,3.91E-6,4.07E-6,4.57E-6

ALPT=3.56E-6,3.73E-6,3.91E-6,4.07E-6,4.57E-6

# ------- User constitutive model example

MAT=Al(6061-0)

CMOD=99

NPE=2 NPV=6

NTP=6

TEM=21.0,148.9,204.4,260.0,371.1,400.0

E1=72.5E9,69.4E9,65.8E9,58.5E9,41.5E9,41.5E9

E2=0.33,0.33,0.33,0.33,0.33,0.33

ALPA=22.5E-6,22.5E-6,22.5E-6,22.5E-6,22.5E-6,22.5E-6

ALPT=22.5E-6,22.5E-6,22.5E-6,22.5E-6,22.5E-6,22.5E-6

V1=1.E4, 1.E4, 1.E4, 1.E4, 1.E4, 1.E4

V2=100.E6,100.E6,100.E6,100.E6,100.E6,100.E6

V3=190.E6,190.E6,190.E6,190.E6,190.E6,190.E6

V4=70.0,70.0,70.0,70.0,70.0,70.0

V5=10.0,7.0,4.0,1.6,0.55,0.55

V6=0.4,0.4,0.4,0.4,0.4,0.4

Annotated Input Data

1) Flags: None

2) Constituent material information

a) External material database file specification (*MDBPATH) [KM_2]:

Name of exernal database file: sample_material_database.mat

(NAME=sample_material_database.mat)

b) Constituent materials to include for code execution (*CONSTITUENTS) [KM_2]:

Number of materials: 3 (NMATS=3)

Constitutive models: Bodner-Partom (CMOD=1)

User-defined (CMOD=99)

Linear Elastic (CMOD=6)

Materials: All User-defined: (MATID=U)

Copper (EXTMAT=copper)

Al 6061-0 (EXTMAT=Al(6061-0))

SCS-6 fiber (EXTMAT=SCS-6)

Material property source: External material database (MATDB=3)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Monolithic material (MOD=1)

Material assignment: Each constituent successively (M=*)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 23., 23. °C (TEMP=23.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 0.02 sec. (STP=0.02)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 20 (FREQ=20)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_2h (NAME=example_2h)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

The results for this example problem, in the form of the three stress-strain curves for the three constituent materials, are given in Figure 2.12. It is again important to note that, since the Al 6061-0 material employs the distributed version of the usrmat.F90 subroutine and the usrformde.F90 subroutine, if an altered version of these subroutines is called by MAC/GMC 4.0, this example problem may not execute correctly.

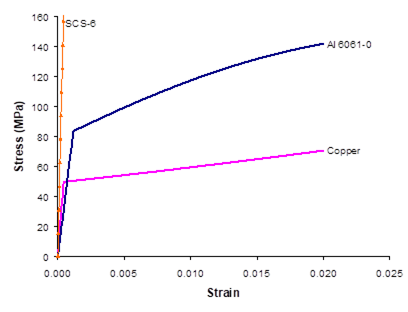
Figure 2.12 Example 2h: plot of the tensile stress-strain response for three materials taken from the external material database.

Section 3 : Analysis Type and Architecture

This section presents example problems that demonstrate the variations in the type of micromechanics analysis and composite architecture that can be analyzed with MAC/GMC 4.0. Two keywords, only one of which may appear in any given input file, specify the analysis type and architecture: *RUC and *LAMINATE. A fundamental difference exists between problems using these two keywords. *RUC indicates that the problem is associated with a repeating unit cell analysis – it is a continuum or effective medium, without any boundaries, that is simulated. *LAMINATE on the other hand, indicates that MAC/GMC is simulating a laminated plate structure (with the use of classical lamination theory) that has a finite through-thickness dimension and top and bottom boundaries. The effective medium that constitutes each layer of the laminate is then analyzed with its own repeating unit cell analysis on this local scale.

Within repeating unit cell analysis, several variations of the analysis type are possible, as indicated by MOD=*. The simplest type of analysis, which was used extensively in the example problems of Section 2, is that of a monolithic material. Internally within MAC/GMC, monolithic material analysis actually employs the doubly periodic GMC micromechanics model using a single subcell as the repeating unit cell. The repeating unit cell analysis type may also be specified as doubly periodic GMC or triply periodic GMC. The doubly periodic GMC model simulates unit cell geometries that are repeating in the two in-plane coordinate directions, but are constant in the out-of-plane coordinate direction. Triply periodic GMC simulates unit cell geometries that are repeating in all three coordinate directions. Hence, doubly periodic GMC can be used to analyze continuous fiber composites, while triply periodic GMC can be employed for discontinuous or particulate composites. Finally, a new doubly periodic micromechanics model is also available in MAC/GMC 4.0. This is high-fidelity GMC (HFGMC). As discussed in the MAC/GMC 4.0 Theory Manual, this new micromechanics model is more accurate in terms of the micro scale fields compared to GMC. However, GMC is considerably more computationally efficient than HFGMC. Example problems using doubly and triply periodic GMC unit cell analyses are presented in this section, along with an HFGMC analysis example.

Laminate analysis within MAC/GMC 4.0 may be thought of as a global or structural scale approach, within which GMC is embedded. The laminate is composed of layers that can each be a composite material. The composite material within each layer is then modeled using doubly or triply periodic GMC. If the laminate is linearly elastic and is not subject to any damage or failure, GMC is merely utilized to determine the effective elastic properties of each layer. In the presence of inelasticity, however, the inelastic constitutive model (in general) must be evaluated on the level of each individual subcell within the GMC analysis of a given ply. Thus, as the simulated loading is applied to the laminate in an incremental fashion, localization from the laminate, to the plies, to the repeating unit cells, to the subcells must occur. The local inelastic strains can then be calculated for the subcells and then globalized (through homogenization) to the repeating unit cell, to the plies, and to the laminate. Thus, this localization/globalization process proceeds at each step of the incrementally applied simulated loading on the laminate. If the incremental plasticity constitutive model is employed, the localization/globalization process occurs for each iteration at each step of the applied loading. Several inelastic laminate analysis example problems are given in this section.

Example 3a: Doubly Periodic GMC Internal RUC Library

This example problem illustrates how to utilize the internal library of doubly periodic repeating unit cell architectures within MAC/GMC 4.0. The thermal and mechanical loading conditions, materials, and fiber volume fraction remain constant for use with all repeating unit cell architectures with the exception of ARCHID=9, which represents a composite with two different sized fibers, each with its own volume fraction. Some of the architectures addressed in this example may also be utilized with an interface present between the fiber and the matrix. This interface is composed of a third material that must be specified in *CONSTITUENTS. Example 3b analyzes doubly periodic unit cell architectures that do include this distinct interfacial phase. For more information on the code’s repeating unit cell architectures, see the MAC/GMC 4.0 Keywords Manual Section 3.

MAC/GMC Input File: example_3a.mac

MAC/GMC 4.0 Example 3a - Doubly Periodic GMC RUC Library

*CONSTITUENTS

NMATS=3

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

M=3 CMOD=6 MATID=D

*RUC

MOD=2 ARCHID=1 VF=0.25 F=1 M=2

# MOD=2 ARCHID=2 VF=0.25 F=1 M=2

# MOD=2 ARCHID=3 VF=0.25 F=1 M=2

# MOD=2 ARCHID=4 XA=0.2 VF=0.25 F=1 M=2

# MOD=2 ARCHID=6 R=1.0 VF=0.25 F=1 M=2

# MOD=2 ARCHID=7 R=1.0 VF=0.25 F=1 M=2

# MOD=2 ARCHID=9 VF1=0.1 RAD1=50. VF2=0.15 RAD2=71. R=1. F=3,1 M=2

# MOD=2 ARCHID=11 R=2.0 VF=0.25 F=1 M=2

# MOD=2 ARCHID=13 R=1.0 VF=0.25 F=1 M=2

*MECH

LOP=2

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=1

NAME=example_3a X=2 Y=8

MICRO=0

*END


	ARCHID = 0

ARCHID = 1	ARCHID = 2	ARCHID = 3

ARCHID = 4	ARCHID = 6	ARCHID = 7

ARCHID = 9	ARCHID = 11	ARCHID = 13

Figure 3.1 MAC/GMC 4.0 doubly periodic repeating unit cell (RUC) architecture library.

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 3 (NMATS=3)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Boron fiber (MATID=D)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: isotropic GVIPS (CMOD=4)

Boron fiber: linearly elastic (CMOD=6)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: square fiber, square pack (ARCHID=1)

Square fiber, hexagonal pack (ARCHID=2)

Square fiber, square diagonal pack (ARCHID=3)

Cross shaped fiber, square pack (ARCHID=4)

7´7 circular fiber approx., rectangular pack (ARCHID=6)

14´14 circular fiber approx., rectangular pack (ARCHID=7)

2 different size square fibers, rectangular pack (ARCHID=9)

Square fiber, rectangular pack (ARCHID=11)

26´26 circular fiber approx., rectangular pack (ARCHID=13)

Fiber volume fractions: 0.25 (VF=0.25)

ARCHID=9: Boron = 0.15 SiC = 0.10 (VF1=0.15

VF2=0.1)

Unit cell aspect ratio: 1.0 (square pack), 2.0 for ARCHID=11 (R=1.0 or R=2.0)

Fiber Radii: 50 mm, 71mm (ARCHID=9 only) (RAD1=50 RAD2=71)

Cross arm length: 0.2 (ARCHID=4 only) (XA=0.2)

Material assignment: SiC fiber (F=1 or F1=1)

Ti-21S matrix (M=2)

Boron fiber (ARCHID=9 only) (F=3)

All 9 doubly periodic fiber architectures contained in the MAC/GMC 4.0 library are exercised in this example problem. Each architecture can be used by commenting and uncommenting the appropriate lines of the input file. ARCHID=9 is a special case in that it requires 2 fibers with different radii. Note that, while the fiber radii are specified, only the size of the two fibers relative to each other is important, not the actual radii themselves. In addition, because ARCHID=9 requires the packing of the two fibers to be square or rectangular, not all geometries are possible. As such, the fiber volume fraction of the second fiber, the SiC fiber in this example, is adjusted from the specified value to allow the packing arrangement to be correct given the value of the first fiber’s volume fraction and the unit cell aspect ratio, R. Finally, for the cross shaped fiber, ARCHID=4, the cross arm length, XA, is the ratio of the length of the arm of the cross to the total length of the cross, where the total length of the cross is set to 1.0 (see Figure 3.1). For more information on these fiber architectures, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_3a (NAME=example_3a)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 3.2 shows the effect of refining the fiber cross-section representation within the repeating unit cell for the square fiber packing arrangement. ARCHID=1 is the least refined fiber representation wherein the fiber is a square. Then, the fiber representation becomes more circular for ARCHID=4, ARCHID=6, ARCHID=7, and ARCHID=13. For the case of the transverse tensile response of a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C, convergence based on the circular fiber refinement occurs quickly – the cross shaped, 7´7, 14´14, and 26´26 representations give nearly identical results.

Figure 3.3 shows that the hexagonal and rectangular packing arrangements also give nearly identical results for this example. The large aspect ratio (R=2.0) employed with ARCHID=11, however, does have a noticeable effect on the composite response. Since the hybrid composite represented by ARCHID=9 is a completely different material system, direct comparison with the other results in this example problem is not possible.

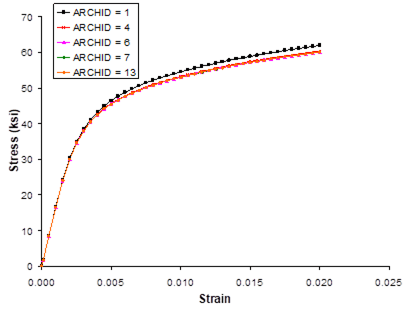
Figure 3.2 Example 3a: plot of the transverse tensile stress-strain (s₂₂-ε₂₂) response for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C as represented by repeating unit cell architectures 1, 4, 6, 7, and 13 from the MAC/GMC 4.0 architecture library.

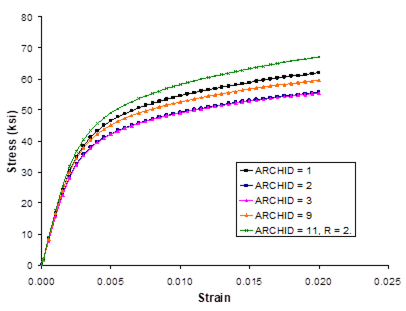
Figure 3.3 Example 3a: plot of the transverse tensile stress-strain (s₂₂-ε₂₂) response for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C as represented by repeating unit cell architectures 1, 2, 3, and 11 from the MAC/GMC 4.0 architecture library, plus the response of a hybrid 0.15 Boron - 0.07439 SiC / Ti-21S composite.

Example 3b: Doubly Periodic RUC Library with Interface

This example problem illustrates the internal library of doubly periodic repeating unit cell architectures within MAC/GMC 4.0 that include a distinct interfacial phase. While the applied loading employed in this example is identical to Example 3a, an additional material is present here that was not in this previous example. This additional material (with user-input material properties) is used for the interface within the analyzed composites. For more information on the code’s repeating unit cell architectures, see the MAC/GMC 4.0 Keywords Manual Section 3.

MAC/GMC Input File: example_3b.mac

MAC/GMC 4.0 Example 3b - Doubly Periodic GMC RUCs w/ interface

*CONSTITUENTS

NMATS=4

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

M=3 CMOD=4 MATID=U MATDB=1 &

EL=11700.,11700.,0.365,0.365,4285.7,1.E-6,1.E-6 &

VI=0.8E-8,0.1,0.1E-5,0.85E-3,0.05,3.3,1.8,1.35,0.1,0.,0.

M=4 CMOD=6 MATID=D

*RUC

MOD=2 ARCHID=1 VF=0.25 RAD=71. RITFR=0.1 F=1 M=2 I=3

# MOD=2 ARCHID=2 VF=0.25 RAD=71. RITFR=0.1 F=1 M=2 I=3

# MOD=2 ARCHID=3 VF=0.25 RAD=71. RITFR=0.1 F=1 M=2 I=3

# MOD=2 ARCHID=6 R=1.0 VF=0.25 RITFR=0.1 F=1 M=2 I=3

# MOD=2 ARCHID=9 VF1=0.10 RAD1=50. RITFR1=0.1 &

# VF2=0.15 RAD2=71. RITFR2=0.1 R=1. F=4,1 M=2 I=3,3

# MOD=2 ARCHID=11 R=2.0 VF=0.25 RAD=71. RITFR=0.1 F=1 M=2 I=3

*MECH

LOP=2

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=0.01

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=1

NAME=example_3b X=2 Y=8

MICRO=0

*END



ARCHID = 1	ARCHID = 2

ARCHID = 3	ARCHID = 6

ARCHID = 9	ARCHID = 11

Figure 3.4 MAC/GMC 4.0 doubly periodic repeating unit cell (RUC) architecture with interface library.

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 4 (NMATS=4)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Fictional interface material (MATID=U)

Boron fiber (MATID=D)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: isotropic GVIPS (CMOD=4)

Interface: isotropic GVIPS (CMOD=4)

Boron fiber: linearly elastic (CMOD=6)

Source for user props: Read from input file (MATDB=1)

A material intended to serve as the interface has been specified using user-defined material properties in conjunction with the isotropic GVIPS constitutive model. This material has been given elastic properties identical to Ti-21S at 650 °C, but its viscoplastic properties cause the material to flow to a much greater extent than does the Ti-21S matrix. This situation is intended to simulate the behavior of a weak interfacial bond within the composite. An example of an alternative more computationally efficient approach to simulating this weak interfacial behavior is examined in Example Problem 5e.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: Square fiber, square pack (ARCHID=1)

Square fiber, hexagonal pack (ARCHID=2)

Square fiber, square diagonal pack (ARCHID=3)

7´7 circular fiber approx., rectangular pack (ARCHID=6)

2 square fibers of different size, square pack (ARCHID=9)

Square fiber, rectangular pack (ARCHID=11)

Fiber volume fractions: 0.25 (VF=0.25)

ARCHID=9: Boron = 0.15 SiC = 0.10 (VF1=0.15

VF2=0.1)

Unit cell aspect ratio: 1.0 (square pack), 2.0 for ARCHID=11 (R=1.0 or R=2.0)

Fiber Radii: SiC fiber: 71mm (RAD=71 or RAD2=71)

Boron fiber: 50 mm (RAD1=50)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

Interface material (I=3)

Boron fiber (ARCHID=9 only) (F=4)

All six doubly periodic fiber architectures contained in the MAC/GMC 4.0 library that included a distinct interface are exercised in this example problem. Each architecture can be used by commenting and uncommenting the appropriate lines of the input file. As in Example 3a, ARCHID=9 is a special case in that it requires 2 fibers with different radii as well as two interfaces. In addition, because ARCHID=9 requires the packing of the two fibers to be square or rectangular, not all geometries are possible. As such, the fiber volume fraction of the second fiber, the SiC fiber in this example, is adjusted from the user specified value to allow the packing arrangement to be correct given the value of the first fiber’s volume fraction and the unit cell aspect ratio, R. For more information on these fiber architectures, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_3b (NAME=example_3b)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 3.5 shows that, when compared to Figure 3.2 and Figure 3.3, that the inclusion of the weak interface within the MAC/GMC repeating unit cell architecture has a major impact on the simulated transverse response of the composite. As stated earlier, an alternative approach to simulating composites with weak fiber-matrix interfaces is presented in Example 5e.

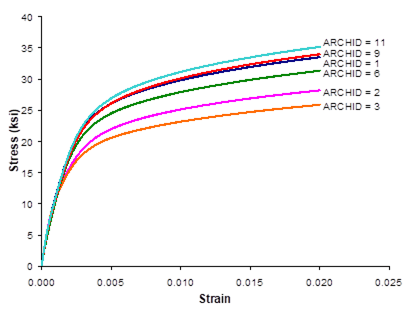
Figure 3.5 Example 3b: plot of the transverse tensile stress-strain (s₂₂-ε₂₂) response for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C as represented by repeating unit cell architectures MAC/GMC 4.0 architecture library, plus the response of a hybrid 0.15 Boron - 0.07439 SiC / Ti-21S composite, all with interfaces.

Example 3c: User-Defined Doubly Periodic Architecture

This example problem illustrates how users may input their own repeating unit cell architecture through the MAC/GMC 4.0 input file. In particular, a B/Al composite with randomly distributed fibers (see Figure 3.6) subjected to an applied strain at a (fast) rate of 0.1/s is considered. For more information on the user-defined repeating unit cell architecture, see the MAC/GMC 4.0 Keywords Manual Section 3.

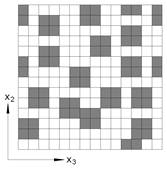
Figure 3.6 Example 3c: Random fiber composite architecture specified through the input file.

MAC/GMC Input File: example_3c.mac

MAC/GMC 4.0 Example 3c - Random composite architecture using 2-D GMC

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 TREF=21. MATID=A

M=2 CMOD=1 TREF=21. MATID=C

*RUC

MOD=2 ARCHID=99

NB=14 NG=14

H=1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.

L=1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.,1.

SM=1,2,2,2,2,2,1,1,2,2,1,1,2,1

SM=1,2,1,1,2,2,1,1,2,2,2,2,2,1

SM=2,2,1,1,2,2,2,2,2,2,1,1,2,2

SM=2,2,2,2,2,2,2,1,1,2,1,1,2,2

SM=2,2,1,1,2,2,2,1,1,2,2,2,2,2

SM=1,2,1,1,2,2,2,2,2,2,1,1,2,1

SM=1,2,2,2,2,1,1,2,2,2,1,1,2,1

SM=2,2,2,2,2,1,1,2,2,2,2,2,2,2

SM=2,1,1,2,2,2,2,2,1,1,2,1,1,2

SM=2,1,1,2,1,1,2,2,1,1,2,1,1,2

SM=2,2,2,2,1,1,1,1,2,2,2,2,2,2

SM=1,1,2,2,2,2,1,1,2,2,2,1,1,2

SM=1,1,2,2,2,2,2,2,2,2,2,1,1,2

SM=2,2,2,2,2,2,2,2,2,2,1,1,2,2

*MECH

LOP=2

NPT=2 TI=0.,0.1 MAG=0.,0.01 MODE=1

*SOLVER

METHOD=1 NPT=2 TI=0.,0.1 STP=0.00005

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=1

NAME=example_3c X=2 Y=8

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: Boron fiber (MATID=A)

Aluminum (6061-0a) (MATID=C)

Constitutive models: Boron fiber: linearly elastic (CMOD=6)

Al matrix: Bodner-Partom (CMOD=1)

Reference Temperature: 21. °C (TREF=21)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

Architecture: User-defined (ARCHID=99)

No. subcells in x₂-dir.: 14 (NB=14)

No. subcells in x₃-dir.: 14 (NG=14)

Subcell heights: 1. (H=1.,1.,…)

Subcell lengths: 1. (L=1.,1.,…)

Material assignment: see input file (SM=…)

The materials that occupy each subcell are specified with SM=…. Each separate SM=… line corresponds to a different descending value of b, while the comma separated material numbers on a given line correspond to different ascending g values. For more information on the user-defined repeating unit cell architecture, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 0.1 sec. (TI=0.,0.1)

Load magnitude: 0., 0.01 (MAG=0.,0.01)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM): None

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 0.1 sec. (TI=0.,0.1)

Time step sizes: 0.00005 sec. (STP= 0.00005)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_3c (NAME=example_3c)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

The results for this example problem are plotted in Figure 3.7. For this composite with randomly distributed strongly bonded fibers, GMC works well. Note, however, that in the presence of a weak interface or fiber-matrix debonding, however, the lack of normal-shear field coupling in GMC would result in significant inaccuracies in the predicted transverse composite response. Such a composite could be modeled more accurately using the high-fidelity GMC (HFGMC) model, which does include the normal-shear field coupling. Example Problem 3f illustrates the use of HFGMC within MAC/GMC 4.0.

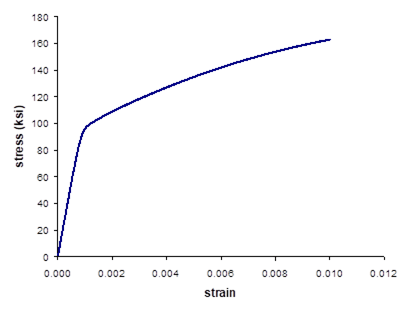
Figure 3.7 Example 3c: plot of the simulated transverse tensile stress-strain (σ₂₂-ε₂₂) response for a 0.3469 fiber volume fraction B/Al composite at 21 °C as represented by a user-defined repeating unit cell architecture intended to simulate randomly distributed fibers.

Example 3d: Triply Periodic GMC Internal RUC Library

This example problem illustrates how to access the internal library of triply periodic repeating unit cell architectures within MAC/GMC 4.0. The loading conditions, materials, and fiber volume fraction remain constant for use with all repeating unit cell architectures. For more information on the code’s internal repeating unit cell architectures, see the MAC/GMC 4.0 Keywords Manual Section 3.


ARCHID = 1	ARCHID = 2		ARCHID = 3

ARCHID = 4		ARCHID = 10

Figure 3.8 MAC/GMC triply periodic repeating unit cell architecture library.

MAC/GMC Input File: example_3d.mac

MAC/GMC 4.0 Example 3d - Triply Periodic GMC RUC Library

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=3 ARCHID=1 VF=0.25 ASP=2. F=1 M=2

# MOD=3 ARCHID=2 VF=0.25 ASP1=2. ASP2=2. F=1 M=2

# MOD=3 ARCHID=3 VF=0.25 ASP1=2. ASP2=1. DR=1. F=1 M=2

# MOD=3 ARCHID=4 VF=0.25 &

# OPT=3 RA=2. RC=1. D=2. H=1. LL=1. F=1 M=2

# MOD=3 ARCHID=10 VF=0.25 F=1 M=2

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=1

NAME=example_3d X=1 Y=7

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Triply periodic GMC (MOD=3)

RUC architecture: 2´2´2, short fiber, square array (ARCHID=1)

Non-overlapping fibers, square diagonal array (ARCHID=2)

Off-set short fibers, square array (ARCHID=3)

Ellipsoidal fiber approximation, rect. array (ARCHID=4)

Open cell (ARCHID=10)

Fiber volume fractions: 0.25 (VF=0.25)

Fiber aspect ratio 2. (ASP=2. or ASP1=2.)

Unit cell aspect ratio: 2. or 1. (ASP=1. or ASP=2.0)

D ratio (ARCHID=3 only): 1. (DR=0.25)

Ellipsoid inclusion:

RUC dimensions: 2., 1., 1. (D=2. H=1. LL=1.)

Semi-major axis ratios: a/b = 2., c/b = 1. (RA=2. RC=1.)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

All five triply periodic repeating unit cell architectures contained in the MAC/GMC 4.0 library are exercised in this example problem. Again, each architecture can be used by commenting and uncommenting the appropriate lines of the input file. ARCHID=1 through ARCHID=3 represent different packing arrangements for short fiber composites wherein the fiber cross-section is square. ARCHID=4 represents an ellipsoidal inclusion, which may be thought of as a three-dimensional generalization of the doubly periodic ARCHID=6. Finally, ARCHID=10 represents a three-dimensional open cell architecture. Diagrams of these architectures are given in Figure 3.8 below. For more information on these fiber architectures, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_3d (NAME=example_3d)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 3.9 shows the simulated response of the triply periodic RUC architectures for this 0.25 fiber volume fraction metal matrix composite. It should be noted that, as the fiber volume fraction of triply periodic composites rises, the GMC predictions can become less accurate. This has been shown by Pahr and Arnold (2002). As the fiber volume fraction rises, the RUC architecture may have thin matrix subcells adjacent to or in between larger fiber subcells. This can cause the theory to over-predict the stress in these thin matrix subcells, which leads to an over-prediction of the inelastic deformation in these subcells and an overall response that is too compliant.

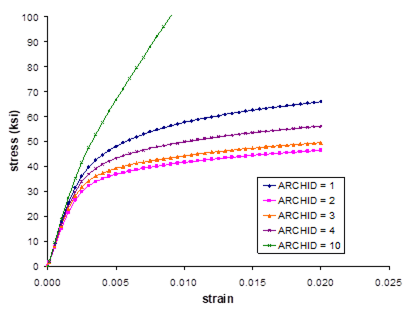
Figure 3.9 Example 3d: plot of the longitudinal tensile stress-strain (s₁₁-e₁₁) response for a 0.25 fiber volume fraction triply periodic SiC/Ti-21S composite at 650 °C as represented by the triply periodic repeating unit cell architectures from the MAC/GMC 4.0 architecture library. See Figure 3.8 for the RUC architectures.

Example 3e: User-Defined Triply Periodic GMC Architecture

This example problem demonstrates how users can input their own triply periodic repeating unit cell architecture. In particular, a periodic [0°/90°] fiber architecture subjected to an applied strain of 0.02 at 650 °C is analyzed. The geometry of the repeating unit cell is shown in Figure 3.10. It should be noted that while the fiber architecture contains 0° and 90° fibers, this problem does not truly simulate a laminate. The represented material is periodic, so it repeats in all three coordinate directions to form a continuum. Therefore, although the RUC has an appearance similar to that of an asymmetric [0°/90°] laminate, no bending will result. A laminate is different in that it has a finite thickness, and the lamination theory formulation is based on a plane stress condition. See the MAC/GMC 4.0 Keywords Manual Section 3 for additional information on the code’s repeating unit cell architectures.

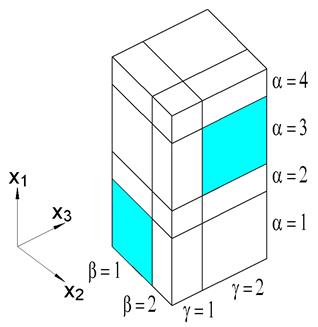
Figure 3.10 Geometry of the user-defined repeating unit cell architecture employed in Example 3e to simulate the response of a periodic [0°/90°] composite.

MAC/GMC Input File: example_3e.mac

MAC/GMC 4.0 Example 3c - [0/90] architecture using 3-d gmc

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=3 ARCHID=99

NA=4 NB=2 NG=2

D=0.67823,0.32177,0.67823,0.32177

H=0.67823,0.32177

L=0.32177,0.67823

# -- gamma = 1

SM=2,2

SM=1,2

# -- gamma = 2

SM=2,2

SM=1,1

SM=2,2

SM=1,2

*MECH

LOP=1

# LOP=2

# LOP=3

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=3

NAME=example_3e_11 X=1 Y=7

NAME=example_3e_22 X=2 Y=8

NAME=example_3e_33 X=3 Y=9

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Triply periodic GMC (MOD=3)

Architecture: User-defined (ARCHID=99)

No. subcells in x1-dir.: 4 (NA=4)

No. subcells in x2-dir.: 2 (NB=2)

No. subcells in x3-dir.: 2 (NG=2)

Subcell depths: see input file (D=0.67823,…)

Subcell heights: see input file (H=0.67823,…)

Subcell lengths: see input file (L=0.32177,…)

Material assignment: see input file (SM=…)

The materials that occupy each subcell are specified with SM=…. The order in which the materials are specified is: 1) ascending groups for each value of g, 2) descending lines for each value of a, and 3) ascending comma separated material numbers for each value of b. That is, in the present example, we have,

# -- gamma = 1

SM=M(4,1,1),M(4,2,1)

SM=M(3,1,1),M(3,2,1)

SM=M(2,1,1),M(2,2,1)

SM=M(1,1,1),M(1,2,1)

# -- gamma = 2

SM=M(4,1,2),M(4,2,2)

SM=M(3,1,2),M(3,2,2)

SM=M(2,1,2),M(2,2,2)

SM=M(1,1,2),M(1,2,2)

where, M(a,b,g) is the material number assigned to subcell (a,b,g). For more information on the user-defined repeating unit cell architecture, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1, 2, or 3 (LOP=1, LOP=2, or, LOP=3)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

F Note: The desired loading option is selected by commenting and uncommenting the appropriate lines of the input file.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_3e_11 (NAME=example_3e_11)

example_3e_22 (NAME=example_3e_22)

example_3e_33 (NAME=example_3e_33)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

ε₂₂, σ₂₂ (X=2 Y=8)

ε₃₃, σ₃₃ (X=3 Y=9)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 3.11 shows that the tensile response of the periodic [0°/90°] composite in the two in-plane coordinate directions (x₂ and x₃) is identical, as expected. In the out-of-plane direction (x₁), the overall tensile response is more compliant due to the absence of continuous reinforcement in this direction.

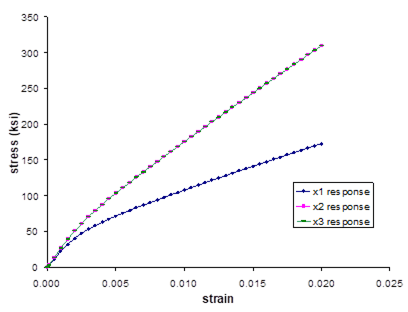
Figure 3.11 Example 3e: plot of the normal tensile stress-strain response in each of the three coordinate directions for a 0.46 fiber volume fraction periodic [0°/90°] SiC/Ti-21S composite at 650 °C as represented by the user-defined triply periodic repeating unit cell architecture shown in Figure 3.10.

Example 3f: High-Fidelity Generalized Method of Cells

This example problem performs analysis of a SiC/Ti-21S composite using the doubly periodic high-fidelity generalized method of cells (HFGMC) and compares the results to those of GMC. In particular, transverse strain is applied to the composite, the 26´26 circular fiber approximation RUC is employed, and the local field results in the composite are examined. HFGMC is formulated using a higher order displacement field than that employed within GMC. This provides HFGMC with normal-shear field coupling that is absent in GMC and allows HFGMC to be more accurate in terms of the local fields. In addition, while the local fields in GMC are piecewise uniform (i.e., constant within each subcell), HFGMC’s local fields vary within the subcells. Thus, in HFGMC all field variables must be tracked not just once for each subcell (as in GMC), but rather at a number of integration points within each subcell. This number of integration points that MAC/GMC 4.0 employs in each subcell, along with the order of the polynomial employed to approximate the inelastic strain field in the composite, must be specified by the user. Because HFGMC employs a higher order displacement field, it requires solution for a greater number of unknowns. This, coupled with the fact that the field variables must be tracked at several integration points within each subcell, renders HFGMC significantly more computationally demanding than GMC. Thus HFGMC’s improved accuracy comes at an increased computational cost over GMC. For more information on HFGMC, see the MAC/GMC 4.0 Theory Manual Section 2.1.2.

MAC/GMC Input File: example_3f.mac

MAC/GMC 4.0 Example 3f - HFGMC doubly periodic analysis

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=12 ARCHID=13 VF=0.25 R=1. F=1 M=2

# MOD=2 ARCHID=13 VF=0.25 R=1. F=1 M=2

*MECH

LOP=2

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

NLEG=5 NINTEG=11

*PRINT

NPL=6

*MATLAB

N=1 TIMES=200.

*XYPLOT

FREQ=5

MACRO=1

NAME=example_3f X=2 Y=8

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic HFGMC (MOD=12)

Doubly periodic GMC (MOD=2)

RUC architecture: 26´26 circular fiber approx., rectangular pack (ARCHID=13)

Fiber volume fractions: 0.25 (VF=0.25)

Unit cell aspect ratio: 1.0 (square pack) (R=1.0)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

By commenting and uncommenting the appropriate lines, HFGMC or GMC may be employed in the present example. It should be noted that the present implementation of the doubly periodic HFGMC model within MAC/GMC 4.0 requires the number of subcells in each direction to be even. If an RUC from the MAC/GMC RUC library that has an odd number of subcells in either direction is selected, an error will occur and execution will stop. For more information on HFGMC, see the MAC/GMC 4.0 Theory Manual Section 2.1.2.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

Order of Legendre polynomial: 5 (NLEG=5)

No. integration points per subcell: 11 (NINTEG=11)

As mentioned above, unlike GMC the local fields within HFGMC vary within each subcell. Thus, a number of integration points (NINTEG) at which to track the field variables within each subcell must be specified. Further, the inelastic strain field is approximated using Legendre polynomials. The order of these polynomials (NLEG) must also be specified. While users may employ desired values for these terms, NLEG=5 and NINTEG=11 have been shown to yield good precision in the local results. It is recommended that these values be employed unless the user is confident in altering them. For more information, see the MAC/GMC 4.0 Keywords Manual Section 4.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) Matlab output data (*MATLAB) [KM_6]:

Number of Matlab output times: 1 (N=1)

Matlab output times: 200. sec. (TIMES=200.)

In order to display the local fields generated by the GMC and HFGMC models in the present example, the *MATLAB keyword has been utilized. This option generates data files containing the local fields within the composite that can be used to generate surface or “fringe” plots using the MATLAB software product. The user specifies the number of times (N) during the MAC/GMC 4.0 simulation that MATLAB output will be written, as well as the actual output times (TIMES) themselves. For more information on generating MATLAB fringe plots like those shown in this example, see the MAC/GMC Keywords Manual Section 6 and Example Problem 6c in this manual.

c) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_3f (NAME=example_3f)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 3.12 shows that the global transverse tensile response predicted by HFGMC and GMC is very similar. However, the local stress component fields plotted in Figure 3.13 (at an applied load of 0.02 transverse strain) show significant differences between the two models. First, since GMC lacks shear coupling and only normal global stresses and strains are imposed, the shear stress (s₂₃) within the composite is zero everywhere in Figure 3.13a. In contrast, Figure 3.13b shows that HFGMC predicts significant shear stress concentrations near the fiber-matrix interface. Second, GMC predicts in-plane normal stress fields (s₂₂ and s₃₃) that are not only uniform within each subcell, but also constant in rows (along the x₃-axis for s₃₃) or columns (along the x₂-axis for s₂₂) of subcells. This is another manifestation of GMC’s lack of shear coupling. HFGMC, on the other hand, predicts in-plane stress fields that vary throughout the repeating unit cell with noticeable concentrations at various locations.

Figure 3.14 compares the inelastic strain component fields predicted by HFGMC and GMC at an applied load of 0.02 transverse strain. As in the stress fields, HFGMC predicts an in-plain shear concentration at the fiber-matrix interface while GMC predicts zero in-plane inelastic shear strain. Otherwise, the GMC appears to match the HFGMC inelastic strain results quite well, although HFGMC does predict higher magnitude and concentrations near the fiber-matrix interface. The improved local fields predicted by HFGMC will have the greatest effect on the predicted overall composite response when effects that depend strongly on the local fields (e.g., damage, debonding, failure) are included in the simulation.

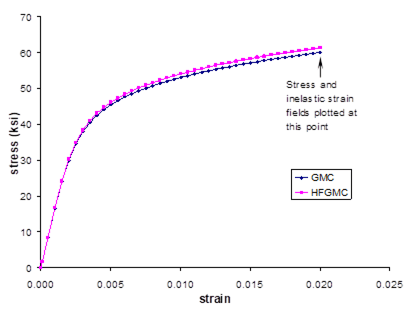
Figure 3.12 Example 3f: plot of the global transverse tensile stress-strain (s₂₂-e₂₂) response for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C as represented by a 26´26 RUC using GMC and HFGMC.

(a)

(b)

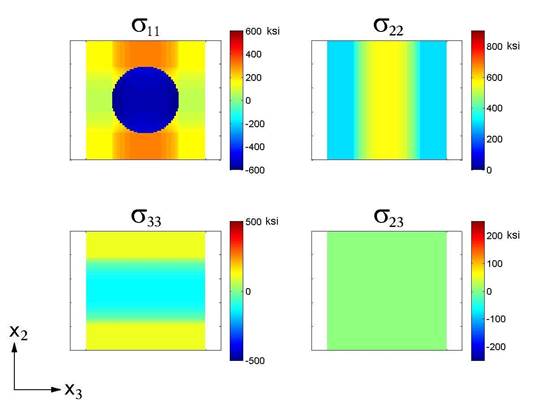
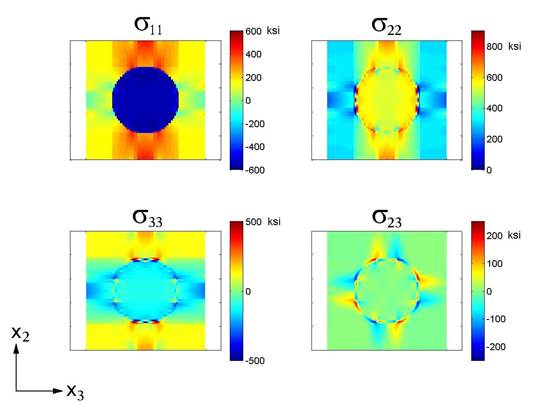
Figure 3.13 Example 3f: plots of the local stress component fields for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C as simulated by (a) GMC and (b) HFGMC at an applied global load of 0.02 transverse strain.

(a)

(b)

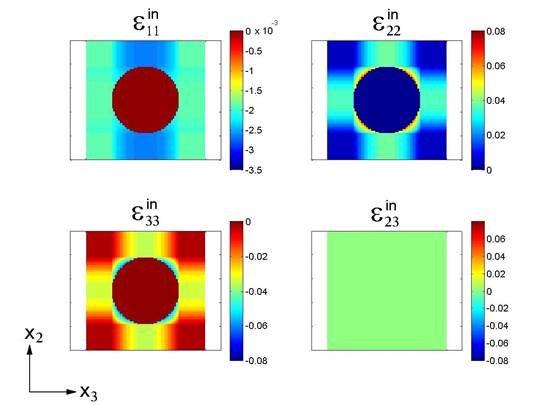
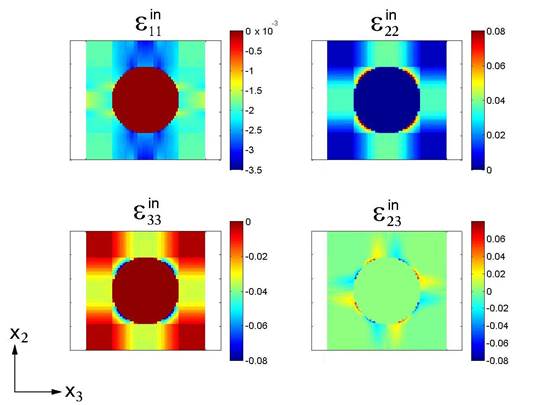
Figure 3.14 Example 3f: plots of the local inelastic strain component fields for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C as simulated by (a) GMC and (b) HFGMC at an applied global load of 0.02 transverse strain.

Example 3g: Laminate Theory – Single Ply

This example problem employs the classical lamination theory capabilities of MAC/GMC 4.0 to simulate the response of a single ply SiC/Ti-21S laminate with several different fiber orientations. It is important to keep in mind that there are several major differences between analyzing a laminate and a composite material, even if both are composed of the same phases. First, while a composite material is a three-dimensional continuum point without edges and boundary influences, a laminate has a finite thickness and thus top and bottom boundaries. Further, classical lamination theory is based on the assumption that the laminate is in a state of plane stress at every point. That is, (in MAC/GMC’s laminate coordinate system, Figure 1.2) the out-of-plane normal stress (s_zz or s₃₃) as well as the out-of-plane shear stresses s_xz and s_yz or s₁₃ and s₂₃) are required to be zero throughout the laminate. Thus global loading that involves any out-of-plane stress (or strain) components is inadmissible. Finally, since the layers within the laminate are composed of composite materials, MAC/GMC 4.0 treats the laminate problem with an embedded multi-scale approach. The local behavior of the composite material in each layer is modeled using GMC, which is embedded within the lamination theory analysis that handles the structural (laminate) scale. For more information on the lamination theory and the code’s laminate analysis capabilities, see the MAC/GMC 4.0 Theory Manual Section 3.

In the present example, a single 0.25 fiber volume fraction SiC/Ti-21S composite ply is considered in which the fiber orientation is varied between 0° (along the x loading direction) and 90° (transverse to the x loading direction). A simple 2´2 square fiber, square pack RUC architecture is employed, and a midplane strain of 0.02 is applied at a temperature of 650 °C.

MAC/GMC Input File: example_3g.mac

MAC/GMC 4.0 Example 3g - Lamination theory, single ply, varying fiber angle

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*LAMINATE

NLY=1

LY=1 MOD=2 THK=1. ANG=0 ARCHID=1 VF=0.25 F=1 M=2

# LY=1 MOD=2 THK=1. ANG=15 ARCHID=1 VF=0.25 F=1 M=2

# LY=1 MOD=2 THK=1. ANG=45 ARCHID=1 VF=0.25 F=1 M=2

# LY=1 MOD=2 THK=1. ANG=30 ARCHID=1 VF=0.25 F=1 M=2

# LY=1 MOD=2 THK=1. ANG=60 ARCHID=1 VF=0.25 F=1 M=2

# LY=1 MOD=2 THK=1. ANG=75 ARCHID=1 VF=0.25 F=1 M=2

# LY=1 MOD=2 THK=1. ANG=90 ARCHID=1 VF=0.25 F=1 M=2

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

LAMINATE=1

NAME=example_3g X=1 Y=10

MACRO=0

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 1 (NLY=1)

Layer analysis model: Doubly periodic GMC (MOD=2)

Layer thickness: 1. (THK=1.)

Layer fiber angle: 0° (ANG=0)

15° (ANG=15)

30° (ANG=30)

45° (ANG=45)

60° (ANG=60)

75° (ANG=75)

90° (ANG=90)

Architecture: 2´2, square fiber, square pack (ARCHID=1)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

The information for each layer is specified on a separate line of the input file. In the present example, the laminate contains only one layer and thus requires only one line. The information on the line is similar to that which is specified under *RUC for repeating unit cell analysis, with the addition of the layer thickness (THK) and the layer fiber orientation angle (ANG). Note that the thickness values are arbitrary, but the laminate force resultants are integrated through the thickness and thus scale with the overall laminate thickness. In order to execute the code for the seven different fiber orientations, the appropriate lines in the input file must be commented and uncommented. For more information on the laminate analysis input requirements, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (loading in the laminate x-direction) (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: midplane strain/curvature control (MODE=1)

Rather than applying loads in the form of stress and strain components as is done in repeating unit cell analysis, in laminate analysis, stress/moment resultants and midplane strains/curvatures are applied. In addition, as mentioned above, only in-plane loading is admissible so the loading options are numbered differently. Loading options 1 – 3 are associated with applied in-plane force resultants or midplane strains. Loading options 4 – 6 are associated with applied in-plane moment resultants or midplane curvatures. For more information on mechanical loading in laminate analysis, see the MAC/GMC 4.0 Keywords Manual Section 4.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of laminate plots: 1 (LAMINATE=1)

Laminate plot name: example_3g (NAME=example_3g)

Laminate plot x-y quantities: , (X=1 Y=10)

Number of macro plots: 0 (MACRO=0)

Number of micro plots: 0 (MICRO=0)

Because this example problem involves a laminate, an additional level of x-y plot output is available above the macro and micro plot output available in repeating unit cell analysis. The number of these laminate scale plots is specified by LAMINATE=. “_lam.data” is appended to the laminate level plot names, thus, in this example, the x-y plot output is written to a file named “example_3g_lam.data”. Note that, since different quantities are available for plotting on the scale of the laminate, the numbering scheme for X= and Y= is different than that used for the macro and micro plots. For more information on generating laminate scale x-y plot files, see the MAC/GMC Keywords Manual Section 6.

7) End of file keyword: (*END)

Results

The following is taken from the MAC/GMC 4.0 output file for this example problem for the 0° ply:

--------------------- EFFECTIVE PROPERTIES AT TEMPERATURE = 650.00 ----------------------------

* FOR LAYER NUMBER 1 *

CG - Effective/Macro Stiffness Matrix

0.3082E+05 0.1277E+05 0.1277E+05

0.1277E+05 0.2517E+05 0.1305E+05

0.1277E+05 0.1305E+05 0.2517E+05

0.5360E+04

0.5719E+04

CI - Effective/Macro Compliance Matrix

0.4488E-04 -0.1500E-04 -0.1500E-04

-0.1500E-04 0.5935E-04 -0.2317E-04

-0.1500E-04 -0.2317E-04 0.5935E-04

0.1866E-03

0.1749E-03

Effective Engineering Moduli

E11S= 0.2228E+05

N12S= 0.3342

E22S= 0.1685E+05

N23S= 0.3903

E33S= 0.1685E+05

G23S= 0.5360E+04

G13S= 0.5719E+04

G12S= 0.5719E+04

Effective Thermal Expansion Coefficients

0.7452E-05 0.1105E-04 0.1105E-04

Local Q Stiffness For Layer 1

2.434E+04 6.150E+03 0.000E+00

6.150E+03 1.840E+04 0.000E+00

0.000E+00 0.000E+00 5.719E+03

Global Q Stiffness For Layer 1

2.434E+04 6.150E+03 0.000E+00

6.150E+03 1.840E+04 0.000E+00

0.000E+00 0.000E+00 5.719E+03

------------------------------------------------------------------------------------------------

----------------------- LAMINATE RESULTS AT TEMPERATURE = 650.00 -------------------------------

Laminate Axial Stiffness Matrix [A]

2.434E+04 6.150E+03 0.000E+00

6.150E+03 1.840E+04 0.000E+00

0.000E+00 0.000E+00 5.719E+03

Laminate Coupling Stiffness Matrix [B]

0.000E+00 0.000E+00 0.000E+00

Laminate Bending Stiffness Matrix [D]

2.028E+03 5.125E+02 0.000E+00

5.125E+02 1.534E+03 0.000E+00

0.000E+00 0.000E+00 4.766E+02

Laminate Engineering Constants (only valid for symmetric laminates)

Exx= 2.228E+04

Nxy= 3.342E-01

Eyy= 1.685E+04

Gxy= 5.719E+03

================================================================================================

***** Section III: Time-Based Output *****

================================================================================================

1 TIME: 1.0000D+00 TEMP: 6.5000D+02 TSTEP: 1.0000D+00

-------------------------------------------------------------------------------------------------------

FORCE(N), MOMENT(M): 2.2280D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

STRAIN, CURVATURE: 1.0000D-04 -3.3418D-05 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

INELASTIC N, M: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

THERMAL N, M: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

OUT-OF-PLANE STRAIN: -3.3418D-05 0.0000D+00 0.0000D+00

ABD MATRIX:

| 2.43355D+04 6.14987D+03 0.00000D+00 0.00000D+00 0.00000D+00 0.00000D+00 |

| 6.14987D+03 1.84029D+04 0.00000D+00 0.00000D+00 0.00000D+00 0.00000D+00 |

| 0.00000D+00 0.00000D+00 5.71872D+03 0.00000D+00 0.00000D+00 0.00000D+00 |

| 0.00000D+00 0.00000D+00 0.00000D+00 2.02796D+03 5.12489D+02 0.00000D+00 |

| 0.00000D+00 0.00000D+00 0.00000D+00 5.12489D+02 1.53357D+03 0.00000D+00 |

| 0.00000D+00 0.00000D+00 0.00000D+00 0.00000D+00 0.00000D+00 4.76560D+02 |

As shown above, for laminate analysis, the output to the MAC/GMC 4.0 output file is different than for repeating unit cell analysis. For each layer, the local (in principal material coordinates) and global (in laminate coordinates) reduced stiffness matrices (Q) are output. Further, the axial, coupling, and bending stiffness matrices (A, B, and D) for the laminate are output, as are the effective (or apparent) engineering properties for the laminate. The time-based output has changed as well. Instead of printing the six components of stress and strain at each time step (as is done for repeating unit cell analysis), for laminate analysis, the three components of force and moment resultant and the three components of midplane strain and curvature are printed. In place of the inelastic and thermal strains, inelastic and thermal force and moment resultants are output. Also, due to the plane stress assumption inherent within classical lamination theory, the out-of-plane stress components are zero throughout the laminate. However, the out-of-plane strain components may or may not (due to Poisson effects) be zero. Thus, these out-of-plane strain components are printed at each time step. Finally, rather than the composite stiffness, the laminate ABD matrix is output at each time step. Note that the above description pertains to a print level of 6 (NPL=6). More or less data is written to the MAC/GMC 4.0 output file if this value is altered (see the Keywords Manual Section 6 for details on the code’s print levels).

Figure 3.15 shows that the [0°] ply, with its fibers oriented along the loading direction, gives the stiffest response. In fact, because a ply thickness of 1. was employed and no bending occurs, the response of the [0°] ply shown in Figure 3.15 is identical to the longitudinal stress-strain response generated for the SiC/Ti-21S composite at 650 °C in Example 1d (Figure 1.5). As the orientation angle of the ply rises from 0°, the response rapidly becomes more compliant as one might expect. However, at the higher angles this trend reverses – the most compliant response is exhibited by the [60°] ply. Then, as the orientation angle continues to rise to 75° and 90°, the ply’s response stiffens. This trend is somewhat counterintuitive as one might expect the response of a [90°] ply, with its fibers oriented completely normal to the loading direction, to be the most compliant orientation. However, as stated by Jones (1974), “the extremum material properties [of a ply] do not necessarily occur in the principal material directions.” Indeed, consider the formula for the apparent stiffness of an off-axis ply (Jones, 1975),

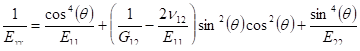
where is the apparent stiffness in the x-direction, and are the longitudinal and transverse ply stiffness (i.e., principal material coordinate stiffnesses), is the ply axial shear modulus, is the ply axial Poisson ration, and is the fiber orientation angle. For the SiC/Ti-21S composite considered in the present example, the ply properties in principal material coordinates (,,, and ) can be obtained from the output file:

Effective Engineering Moduli

E11S= 0.223E+05

N12S= 0.334E+00

E22S= 0.168E+05

N23S= 0.390E+00

E33S= 0.168E+05

G23S= 0.536E+04

G13S= 0.572E+04

G12S= 0.572E+04

Utilizing these values in conjunction with the formula for the apparent ply stiffness (given above) yields a plot of the apparent ply stiffness vs. fiber orientation angle for the 0.25 fiber volume fraction SiC/Ti-21S ply as shown in Figure 3.16. Clearly, the apparent stiffness of the ply first decreases, and then increases as the fiber orientation angle rises. The apparent modulus reaches a minimum at an angle of 55.6 °. Thus the trend shown in Figure 3.15, while somewhat counterintuitive, is correct.

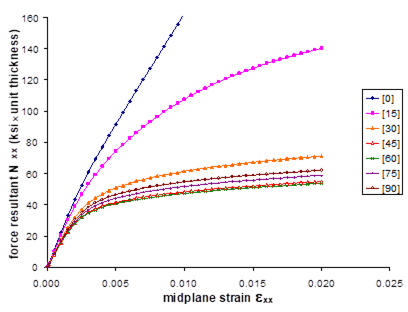
Figure 3.15 Example 3g: plot of the global tensile force resultant – midplane strain () response for a 0.25 fiber volume fraction single ply SiC/Ti-21S laminate at 650 °C with varying fiber orientation angle.

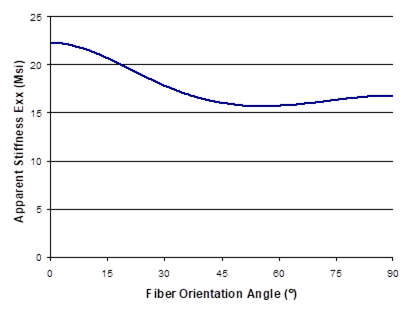
Figure 3.16 Example 3g: plot of the apparent stiffness of a 0.25 fiber volume fraction SiC/Ti-21S ply at 650 °C as a function of fiber orientation angle.

Example 3h: Cross-Ply and Quasi-Isotropic Laminates

This example problem employs the classical lamination theory capabilities of MAC/GMC 4.0 to simulate the response of two SiC/Ti-21S laminates: cross-ply [90°/0°]_s and quasi-isotropic [90°/45°/0°/-45°]_s. As in Example 3g, a midplane strain of 0.02 is applied to the laminate, however, in the present problem a more refined RUC architecture is employed for each layer. For more information on the lamination theory and the code’s laminate analysis capabilities, see the MAC/GMC 4.0 Theory Manual Section 3.

MAC/GMC Input File: example_3h.mac

MAC/GMC 4.0 Example 3h - Cross-ply and quasi-isotropic laminates

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*LAMINATE

# -- Cross-ply

NLY=3

LY=1 MOD=2 THK=0.25 ANG=90 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=2 MOD=2 THK=0.50 ANG=0 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=3 MOD=2 THK=0.25 ANG=90 ARCHID=6 R=1. VF=0.25 F=1 M=2

# -- Quasi-isotropic

# NLY=7

# LY=1 MOD=2 THK=0.125 ANG=90 ARCHID=6 R=1. VF=0.25 F=1 M=2

# LY=2 MOD=2 THK=0.125 ANG=45 ARCHID=6 R=1. VF=0.25 F=1 M=2

# LY=3 MOD=2 THK=0.125 ANG=0 ARCHID=6 R=1. VF=0.25 F=1 M=2

# LY=4 MOD=2 THK=0.25 ANG=-45 ARCHID=6 R=1. VF=0.25 F=1 M=2

# LY=5 MOD=2 THK=0.125 ANG=0 ARCHID=6 R=1. VF=0.25 F=1 M=2

# LY=6 MOD=2 THK=0.125 ANG=45 ARCHID=6 R=1. VF=0.25 F=1 M=2

# LY=7 MOD=2 THK=0.125 ANG=90 ARCHID=6 R=1. VF=0.25 F=1 M=2

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

LAMINATE=1

NAME=example_3h X=1 Y=10

MACRO=0

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Cross-Ply Laminate:

Number of layers: 3 (NLY=3)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Aspect Ratio	Volume fraction	Fiber material	Matrix material
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(R)	(VF)	(F)	(M)
1	GMC-2D	0.25	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
2	GMC-2D	0.50	0°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
3	GMC-2D	0.25	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S

Quasi-Isotropic Laminate:

Number of layers: 7 (NLY=7)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Aspect Ratio	Volume fraction	Fiber material	Matrix material
(LY=)	(MOD=2)	(THK=)	(ANG=)	(ARCHID=6)	(R=1.)	(VF=0.25)	(F=1)	(M=2)
1	GMC-2D	0.125	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
2	GMC-2D	0.125	45°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
3	GMC-2D	0.125	0°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
4	GMC-2D	0.25	-45°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
5	GMC-2D	0.125	0°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
6	GMC-2D	0.125	45°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
7	GMC-2D	0.125	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S

F Note: In order to execute the code for the two different laminates, the appropriate lines in the input file must be commented and uncommented. For more information on the laminate analysis input requirements, see the MAC/GMC 4.0 Keywords Manual Section 3.

F Note: The middle layers of both laminates are twice as thick as the other layers because these layers actually represent two individual layers that are adjacent, and thus can be combined in the analysis.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (loading in the laminate x-direction) (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: midplane strain/curvature control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of laminate plots: 1 (LAMINATE=1)

Laminate plot name: example_3h (NAME=example_3h)

Laminate plot x-y quantitiies: , (X=1 Y=10)

Number of macro plots: 0 (MACRO=0)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Table 3.1 and Figure 3.17 show that the cross-ply laminate exhibits a stiffer global response than does the quasi-isotropic laminate. The difference is especially clear in the post-yield response depicted in Figure 3.17. In addition, from Table 3.1, it is clear that neither laminate exhibits global extensional normal-shear coupling as the terms A₁₆ and A₂₆ are zero (or nearly zero) in both cases. However, since the terms D₁₆ and D₂₆ are non-zero for the quasi-isotropic laminate, normal-shear bending coupling is present, whereas this coupling is absent in the cross-ply laminate. Also plotted in Figure 3.17 is the response of a 0.25 fiber volume fraction SiC/Ti-21S composite whose geometry is represented by a cross-ply continuum architecture (see Figure 3.10) using triply periodic GMC from Example 3e. For the present case, the continuum and lamination theory simulations are in good agreement. Finally, examining the effective laminate engineering constants in Table 1, it is clear why the [90°/45°/0°/-45°]_s laminate is termed “quasi-isotropic”, while the [90°/0°]_s laminate is not. For isotropic materials, the relation among the elastic engineering constants is,

Substituting the effective laminate and engineering constants for the quasi-isotropic laminate results in a calculated isotropic shear modulus value of ksi, which agrees with the value determined for the laminate given in Table 3.1. In contrast, this value calculated for the cross-ply laminate is ksi, which does not agree with the value determined for the laminate in Table 3.1. Thus, the [90°/45°/0°/-45°]s laminate exhibits “quasi-isotropy” in its effective engineering constants, while the [90°/0°]s laminate does not.

Table 3.1 Example 3h: effective stiffness and engineering constant results for the 0.25 volume fraction SiC/Ti-21S laminates analyzed taken from the MAC/GMC 4.0 output file.

Cross-Ply

Quasi-Isotropic

Laminate Axial Stiffness Matrix [A]

2.130E+04 6.108E+03 7.791E-08

6.108E+03 2.130E+04 -6.978E-07

7.791E-08 -6.978E-07 5.704E+03

Laminate Coupling Stiffness Matrix [B]

0.000E+00 0.000E+00 0.000E+00

Laminate Bending Stiffness Matrix [D]

1.586E+03 5.090E+02 1.136E-08

5.090E+02 1.964E+03 -1.018E-07

1.136E-08 -1.018E-07 4.754E+02

Laminate Engineering Constants

E11= 1.955E+04

N12= 2.868E-01

E22= 1.955E+04

G12= 5.704E+03

Laminate Axial Stiffness Matrix [A]

2.035E+04 7.054E+03 3.896E-08

7.054E+03 2.035E+04 -3.489E-07

3.896E-08 -3.489E-07 6.650E+03

Laminate Coupling Stiffness Matrix [B]

0.000E+00 5.684E-14 -2.344E-15

5.684E-14 0.000E+00 1.556E-15

-2.344E-15 1.556E-15 -1.137E-13

Laminate Bending Stiffness Matrix [D]

1.608E+03 5.583E+02 3.542E+01

5.583E+02 1.844E+03 3.542E+01

3.542E+01 3.542E+01 5.246E+02

Laminate Engineering Constants

E11= 1.791E+04

N12= 3.466E-01

E22= 1.791E+04

G12= 6.650E+03

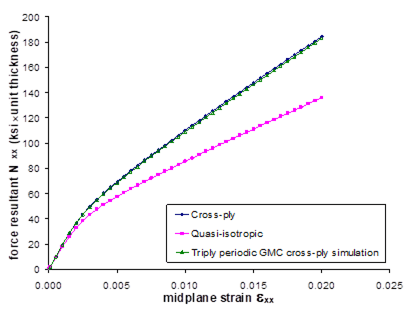
Figure 3.17 Example 3h: plot of the global tensile force resultant – midplane strain () response for 0.25 fiber volume fraction cross-ply [90°/0°]_s and quasi-isotropic [90°/45°/0°/-45°]_s SiC/Ti-21S laminates at 650 °C. Also plotted is a triply periodic GMC prediction using an RUC like that employed in Example 3e that simulates a cross-ply architecture.

Example 3i: Asymmetic Laminate

This example problem employs the classical lamination theory capabilities of MAC/GMC 4.0 to simulate the response of an asymmetric SiC/Ti-21S laminate. This fictional laminate consists of four plies, each of which is different. In fact, one layer is monolithic, one layer employs doubly periodic GMC, and the final two layers employ triply periodic GMC. Note that the ability to include doubly and triply periodic layers within the same laminate is a new capability of MAC/GMC 4.0. The laminate is subjected to a midplane strain of 0.02 at 23 °C. The asymmetric lay up of the laminate plies gives rise to non-zero terms in the laminate coupling stiffness matrix [B], which induces bending when the laminate is subjected to the applied midplane strain. For more information on the lamination theory and the code’s laminate analysis capabilities, see the MAC/GMC 4.0 Theory Manual Section 3.

MAC/GMC Input File: example_3i.mac

MAC/GMC 4.0 Example 3i - Asymmetric laminate

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*LAMINATE

NLY=4

LY=1 MOD=1 THK=0.25 M=2

LY=2 MOD=2 THK=0.25 ANG=60 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=3 MOD=3 THK=0.25 ANG=0. ARCHID=3 ASP1=3. ASP2=2. DR=1. VF=0.25 F=1 M=2

LY=4 MOD=3 THK=0.25 ANG=0. ARCHID=1 VF=0.25 ASP=1. F=1 M=2

*MECH

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=23.,23.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=0.5

*PRINT

NPL=6

*XYPLOT

FREQ=5

LAMINATE=13

NAME=example_3i_nxx X=1 Y=10

NAME=example_3i_nxxp X=1 Y=16

NAME=example_3i_nyyp X=1 Y=17

NAME=example_3i_nxyp X=1 Y=18

NAME=example_3i_mxxp X=1 Y=19

NAME=example_3i_myyp X=1 Y=20

NAME=example_3i_mxyp X=1 Y=21

NAME=example_3i_eyy X=1 Y=2

NAME=example_3i_ezz X=1 Y=3

NAME=example_3i_exy X=1 Y=6

NAME=example_3i_kxx X=1 Y=7

NAME=example_3i_kyy X=1 Y=8

NAME=example_3i_kxy X=1 Y=9

MACRO=0

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 4 (NLY=4)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Volume fraction	Aspect ratio	Fiber material	Matrix material
(LY)	(MOD)	(THK)	(ANG)	(ARCHID)	(VF)	(R)	(F)	(M)
1	monolithic	0.25	–	–	–	–	–	Ti-21S
2	GMC-2D	0.25	60°	7´7 circle, rect. pack	0.25	1.	SiC	Ti-21S
3	GMC-3D	0.25	0°	off-set fibers (3)	0.25	–	SiC	Ti-21S
4	GMC-3D	0.25	0°	short fiber (1)	0.25	–	SiC	Ti-21S

Additional information for layers 3 and 4:

Fiber aspect ratio 3. (ASP1=3.)

Unit cell aspect ratio: 2. or 1. (ASP2=2. or ASP=1.)

D ratio (ARCHID=3 only): 1. (DR=1.)

The laminate in this example problem consists of a monolithic Ti-21S layer and three composite SiC/Ti-21S layers: a 60° continuous layer, a short fiber discontinuous layer, and a particulate discontinuous layer. For more information on the laminate analysis input requirements, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 (loading in the laminate x-direction) (LOP=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: midplane strain/curvature control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 23., 23. °C (TEMP=23.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 0.5 sec. (STP=0.5)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of laminate plots: 13 (LAMINATE=13)

Laminate plot names: example_3i_nxx (NAME=example_3i_nxx)

example_3i_nxxp (NAME=example_3i_nxxp)

example_3i_nyyp (NAME=example_3i_nyyp)

example_3i_nxyp (NAME=example_3i_nxyp)

example_3i_mxxp (NAME=example_3i_mxxp)

example_3i_myyp (NAME=example_3i_myyp)

example_3i_mxyp (NAME=example_3i_mxyp)

example_3i_eyy (NAME=example_3i_eyy)

example_3i_ezz (NAME=example_3i_ezz)

example_3i_exy (NAME=example_3i_exy)

example_3i_kxx (NAME=example_3i_kxx)

example_3i_kyy (NAME=example_3i_kyy)

example_3i_kxy (NAME=example_3i_kxy)

Laminate plot quantities: , (X=1 Y=10)

, (X=1 Y=16)

, (X=1 Y=17)

, (X=1 Y=18)

, (X=1 Y=19)

, (X=1 Y=20)

, (X=1 Y=21)

, (X=1 Y=2)

, (X=1 Y=3)

, (X=1 Y=6)

, (X=1 Y=7)

, (X=1 Y=8)

, (X=1 Y=9)

Number of macro plots: 0 (MACRO=0)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Table 3.2 shows that the asymmetric laminate ABD matrix is fully populated. Thus, due to the applied normal midplane strain, global shear strains (due to the presence of the 60° layer), as well as bending (due to the laminate’s asymmetry) will result.

Figure 3.18 shows plots of the laminate force resultant () and laminate inelastic force resultants () that arise due to the applied normal midplane strain. The point at which the laminate yields is clear in this figure as the inelastic force resultants begin to arise. Also, the inelastic shear force resultant is small relative to the normal inelastic force resultants. Figure 3.19 shows the laminate inelastic moment resultants () that rise during the MAC/GMC 4.0 simulation (which are an indicator of inelastic laminate bending). Again, it is clear that the shear component is smaller than the normal components. The inelastic bending moment component associated with the loading direction () appears to be the dominant component, and several reversals in the history occur during the simulation. These reversals are caused by the onset and progression of inelastic deformation in the layers of the laminate as it bends. Figure 3.20 shows the midplane strain and curvature components that arise in the laminate during the simulation. Again, the shear components are less significant than the normal components. The normal curvature histories exhibit reversals in slope, as do the normal inelastic moment results plotted in Figure 3.19.

Table 3.2 Example 3i: effective stiffness and engineering constant results for the asymmetric SiC/Ti-21S laminate analyzed taken from the MAC/GMC 4.0 output file.

Asymmetric Laminate

Laminate Axial Stiffness Matrix [A]

2.342E+04 8.364E+03 8.295E+01

8.364E+03 2.392E+04 4.308E+02

8.295E+01 4.308E+02 7.570E+03

Laminate Coupling Stiffness Matrix [B]

6.044E+02 1.239E+02 -1.037E+01

1.239E+02 5.176E+02 -5.385E+01

-1.037E+01 -5.385E+01 1.024E+02

Laminate Bending Stiffness Matrix [D]

1.888E+03 6.630E+02 1.728E+00

6.630E+02 1.898E+03 8.974E+00

1.728E+00 8.974E+00 5.857E+02

Laminate Engineering Constants (only valid for symmetric laminates)

E11= 2.029E+04

N12= 3.515E-01

E22= 2.074E+04

G12= 7.541E+03

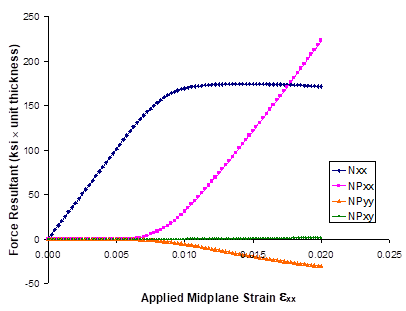
Figure 3.18 Example 3i: plot of the global force resultant (N) and inelastic force resultant (NP) response for an asymmetric SiC/Ti-21S laminate at 23 °C to an applied midplane strain.

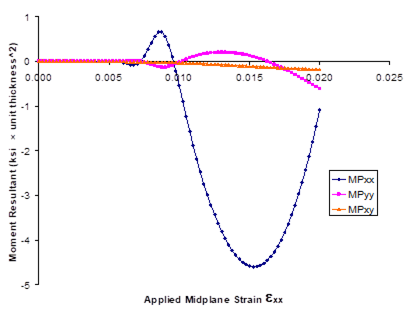
Figure 3.19 Example 3i: plot of the global inelastic moment resultant (MP) response for an asymmetric SiC/Ti-21S laminate at 23 °C to an applied midplane strain.

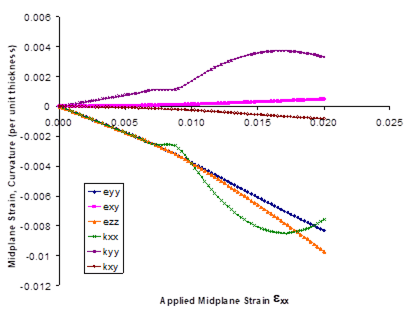
Figure 3.20 Example 3i: plot of the global midplane strain (e) and midplane curvature (k) response for an asymmetric SiC/Ti-21S laminate at 23 °C to an applied midplane strain.

Section 4 : Applied Loading

This section presents example problems demonstrating various ways in which loading may be applied to composites and laminates in MAC/GMC 4.0. To understand the various loading options, it is useful to examine the global, or effective, constitutive equation for a composite material:

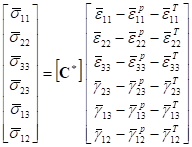
where are the global (or average) stress components on the composite, is the global (or effective) stiffness matrix, are the global (or average) normal strain components on the composite, are the global (or average) normal strain components on the composite, are the global (or average) engineering shear strain components on the composite, are the global (or average) normal inelastic strain components on the composite, are the global (or average) engineering shear inelastic strain components on the composite, are the global (or average) normal thermal strain components on the composite, and are the global (or average) engineering shear thermal strain components on the composite. For repeating unit cell analysis, loading takes the form of an admissible time profile of global stress and strain components. Admissibility simply requires that, if a particular strain component is specified, the corresponding stress component cannot be specified (and vice versa). Thus, the user may specify a time history for each of the six components. Indeed, the arbitrary mechanical loading option within MAC/GMC 4.0 allows just this. However, there are several internal loading options within the code that simplify the application of loading for commonly used mechanical loading types. For instance, a simulated strain controlled tensile test on a composite entails applying a single global strain component (with a corresponding unknown global stress component) while all remaining stress components are kept at zero. MAC/GMC’s internal loading options 1 – 6 allow this type of application of a single load component. Some additional internal loading options simplify biaxial mechanical loading. For details, see the MAC/GMC 4.0 Keywords Manual Section 4.

The loading history that is applied to a laminate is different than that applied to a composite material. Globally, rather than dealing with average stresses and strains, the applicable quantities are stress and moment resultants along with midplane strains and curvatures. For laminate analysis, the code’s internal loading options are numbered differently. Loading options 1 – 3 correspond to application of force resultants or midplane strains in the x₁-x₂ plane, while loading options 4 – 6 correspond to application of moment resultants and curvatures. For additional information on the code’s loading options, see Section

4 of the Keywords Manual.

Example 4a: MAC/GMC Internal Loading Options

This example problem demonstrates all of the internal MAC/GMC 4.0 mechanical loading options that are applicable to repeating unit cell analysis. These internal loading options allow for the easy application of many common uniaxial and biaxial loading conditions. In the present example, doubly periodic GMC is employed in conjunction with loading options 1 through 10. For triply periodic GMC, loading options 1 – 8 are identical to the coinciding doubly periodic GMC loading options. However, loading options 9 and 10 are different, and triply periodic GMC allows two additional loading options, 11 and 12. For more information on the code’s internal mechanical loading options, see the MAC/GMC 4.0 Keywords Manual Section 4.

MAC/GMC Input File: example_4a.mac

MAC/GMC 4.0 Example 4a - RUC analysis internal loading options

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=13 VF=0.25 R=1.25 F=1 M=2

*MECH

LOP=1

# LOP=2

# LOP=3

# LOP=4

# LOP=5

# LOP=6

# LOP=7

# LOP=8

# LOP=9

# LOP=10

# -- Note: LOP > 6 are biaxial & require 2 load profiles

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

# NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=6

NAME=example_4a X=1 Y=7

NAME=example_4a X=2 Y=8

NAME=example_4a X=3 Y=9

NAME=example_4a X=4 Y=10

NAME=example_4a X=5 Y=11

NAME=example_4a X=6 Y=12

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 26´26 circular fiber, rect. pack (ARCHID=13)

Fiber volume fraction: 0.25 (VF=0.25)

RUC aspect ratio: 1.25 (R=1.25)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 11-component (LOP=1)

22-component (LOP=2)

33-component (LOP=3)

23-component (LOP=4)

13-component (LOP=5)

12-component (LOP=6)

11- & 22-components (LOP=7)

22- & 33-components (LOP=8)

11- & 23-components (LOP=9)

22- & 13-components (LOP=10)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

In order to execute the code using each of the ten loading options, the appropriate lines in the input file must be commented and uncommented. For loading options 7 – 10, two load components are applied to the composite simultaneously. Thus, two sets of data are necessary to specify time-magnitude points and the loading mode (i.e., one set for each component). These sets of data are input on two separate lines in the MAC/GMC 4.0 input file. The identical loading history is applied for all loading options in this example. Note that loading options 4 – 6, 9, and 10 involve application of shear strains. MAC/GMC 4.0 employs engineering shear strains (often denoted by g) as opposed to tensorial shear strains (often denoted by e). See Section 4 of the Keywords Manual for additional information on the mechanical loading options.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 6 (MACRO=6)

Macro plot names: example_4a (NAME=example_4a)

Macro plot x-y quantities: , (X=1 Y=7)

, (X=2 Y=8)

, (X=3 Y=9)

, (X=4 Y=10)

, (X=5 Y=11)

, (X=6 Y=12)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 4.1 shows that, among the plots associated with a single applied load component, the normal response of the repeating unit cell in the fiber direction is stiffest, followed by the normal response in the two transverse directions, with the three shear response curves exhibiting significantly more compliance. Figure 4.2 shows the composite response when two strain components are applied simultaneously. Most interesting are the LOP=8 results, which indicate that the composite response is significantly stiffer when and are applied simultaneously compared to when each component is applied individually (see LOP=2 and LOP=3 results in Figure 4.1). This is caused by the constraining effect of the biaxial loading in addition to the higher hydrostatic stress state induced when applying the components simultaneously (which tends to suppress the inelastic deformation in the matrix).

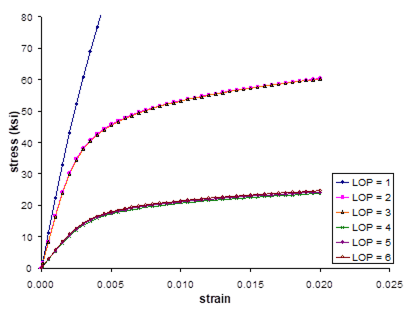
Figure 4.1 Example 4a: plot of the simulated stress-strain response for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C where MAC/GMC 4.0 mechanical loading options 1 – 6 have been employed.

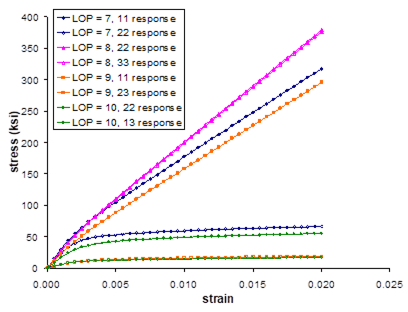
Figure 4.2 Example 4a: plot of the simulated stress-strain response for a 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C where MAC/GMC 4.0 mechanical loading options 7 – 10 have been employed.

Example 4b: SiC/Ti-21S Composite with Residual Stresses

This is an example of a MAC/GMC 4.0 simulation for a metal matrix composite in which residual stresses due to fabrication have been included. The composite configuration is identical to that of Example 1d. The changes lie in the loading section of the input file, wherein, prior to application of the simulated mechanical loading, a simulated stress-free cool-down from 900 °C is performed. Thus, when the simulated mechanical loading is applied, the composite contains internal local stresses within each constituent resulting from property mismatch of the composite phases and the simulated cool-down. The stress-strain curve that results from the subsequent applied mechanical loading can then be shifted such that the origin corresponds to the onset of the mechanical loading. This then simulates an actual composite tensile test in which it is assumed that the zero global strain condition corresponds to the start of the mechanical test.

MAC/GMC Input File: example_4b.mac

MAC/GMC 4.0 Example 4b - SiC/Ti-21S composite w/ residual

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=1 VF=0.25 F=1 M=2

*MECH

LOP=1 REFTIME=57600.

# LOP=2 REFTIME=57600.

NPT=3 TI=0.,57600.,57800. MAG=0.,0.,0.02 MODE=2,1

*THERM

NPT=3 TI=0.,57600.,57800 TEMP=900.,23.,23.

*SOLVER

METHOD=1 NPT=3 TI=0.,57600.,57800 STP=40.,1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=4

NAME=example_4b_11 X=1 Y=7

NAME=example_4b_22 X=2 Y=8

NAME=example_4b_TH1 X=100 Y=1

NAME=example_4b_TH2 X=100 Y=2

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: square fiber, square pack (ARCHID=1)

Fiber volume fraction: 0.25 (VF=0.25)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 or 2 (LOP=1 or LOP=2)

Strain reference time: 57600. sec. (REFTIME=57600.)

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600.,57800.)

Load magnitudes: 0., 0., 0.02 (MAG=0.,0.,0.02)

Loading mode: stress control, strain control (MODE=2,1)

The mechanical loading profile now contains three time-magnitude pairs. For the first segment of the mechanical loading, the magnitude is kept at zero, then, during the second segment, the mechanical loading progresses to a magnitude of 0.02. Since there are now three time-magnitude pairs, and thus two loading segments, two loading modes (one for each segment) must be specified. During the first segment, it is the stress that is held at zero, while during the second segment, it is the strain that is applied up to a level of 0.02.

The strain reference time (REFTIME) is the time taken to be the zero strain point for subsequent specified strains. Thus, the strain that results at time = 57600. sec. from the cool-down is taken as the reference strain. Then, the subsequent applied 0.02 strain is taken with respect to this reference strain such that a total increment in strain of 0.02 is applied. This mimics a tensile stress-strain test on a specimen containing an unknown residual strain. The unknown residual strain is the reference (thought to be zero at the beginning of the tensile test) and the amount of strain applied during the test is on top of this reference strain. If it is not specified, the strain reference time defaults to zero. For additional information on the strain reference time, see the MAC/GMC 4.0 Keywords Manual Section 4.

b) Thermal (*THERM) [KM_4]:

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600.,57800.)

Temperature points: 900., 23., 23. (TEMP=900.,23.,23.)

Three time-temperature pairs are used to specify the two thermal loading segments – a cool-down from 900 °C to 23 °C followed by a hold at 23 °C. The second segment corresponds to the application of the non-zero simulated mechanical loading.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600.,57800.)

Time step size: 40., 1. sec. (STP=40.,1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 4 (MACRO=4)

Macro plot names: example_4b_11 (NAME=example_4b_11)

example_4b_22 (NAME=example_4b_22)

example_4b_TH1 (NAME=example_4b_TH1)

example_4b_TH2 (NAME=example_4b_TH2)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

ε₂₂, σ₂₂ (X=2 Y=8)

Temperature, ε₁₁ (X=100 Y=1)

Temperature, ε₂₂ (X=100 Y=2)

Number of micro plots: 0 (MICRO=0)

In this example, four macro (repeating unit cell level) plots are generated; two represent the mechanical response of the composite, two represent the thermal response of the composite

7) End of file keyword: (*END)

Results

Figure 4.3 shows the strain that results from the simulated stress-free cool-down applied to the SiC/Ti-21S composite. It should be noted that, due to the fact the Ti-21S matrix undergoes inelastic deformation during the cool-down, the overall or global strain plotted in Figure 4.3 is not the global thermal strain. Rather, it is the sum of the global thermal strain and the global inelastic strain. Examining the output file for this example reveals the following global strain state at the conclusion of the simulated cool-down (but before application of the simulated mechanical loading):

1440 TIME: 5.7600D+04 TEMP: 2.3000D+01 TSTEP: 4.0000D+01

-----------------------------------------------------------------------------------------------

STRESS: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

STRAIN: -5.5186D-03 -8.7271D-03 -8.7271D-03 0.0000D+00 0.0000D+00 0.0000D+00

IN. STRAIN: 7.1719D-04 -4.2385D-04 -4.2385D-04 0.0000D+00 0.0000D+00 0.0000D+00

TH. STRAIN: -6.2358D-03 -8.3033D-03 -8.3033D-03 0.0000D+00 0.0000D+00 0.0000D+00

Clearly, there is an inelastic strain contribution to the total strain, in addition to the thermal strain. An interesting ramification of this observation is that, it would be erroneous to use Figure 4.3 to determine tangential coefficients of thermal expansion (CTEs) for the composite by taking slopes of the curves at different temperatures. This would give the slope of the total strain with respect to temperature, while the definition of tangent CTE is the slope of thermal strain with respect to temperature. Taking the slope of an experimental composite thermal expansion curve as a tangential CTE is similarly erroneous if the composite has undergone any inelastic deformation during the test, consequently micromechanics is needed to extract the true composite CTE.

Figure 4.4 shows that the effect of residual stresses on the SiC/Ti-21S composite (at 23 °C) is greater in the longitudinal direction compared to the transverse direction. The composite yields sooner longitudinally for the case that includes residual stresses. In the transverse direction, the simulation with residual stresses exhibits yielding slightly sooner, but the differences in the predicted stress-strain curves is minor. Clearly, the presence of the continuous fibers causes greater residual effects in the longitudinal direction as these fibers have a significant restraining effect on the matrix during the cool down.

It should also be noted that in Figure 4.4, the simulated stress-strain curves with residual stresses have been shifted from the strain value at the completion of the cool-down to a strain value of zero. That is, for example, the composite exhibited a longitudinal strain of -0.00552 upon completion of the cool-down. The longitudinal stress-strain curve with residual in Figure 4.4 was thus shifted to the right by a strain value of +0.00552. Therefore, as is the case in an experimental tensile stress-strain test on a composite, it appears that, at the beginning of the test, the composite starts at zero macro strain. In reality, of course, during manufacture, the composite has experienced some strain, but the as delivered, room-temperature composite state is commonly used as the zero strain reference.

Figure 4.3 Example 4b: plot of the simulated longitudinal and transverse thermal response of a 25% SiC/Ti-21S composite to a stress-free cool-down from 900 °C to 23 °C.

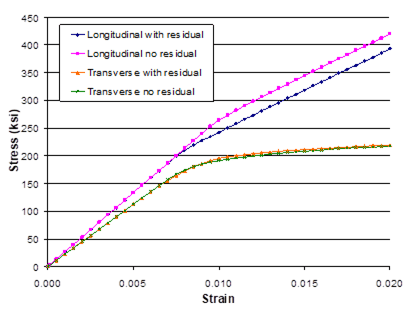
Figure 4.4 Example 4b: plots of the simulated longitudinal and transverse tensile response of a 25% SiC/Ti-21S composite with and without residual stresses included. The plots for the cases without residual stresses are the results from Example 1d.

Example 4c: General Loading Option for RUC analysis

This example demonstrates how to apply a general mechanical loading history to a given repeating unit cell. This option, specified by LOP=99, allows the user to specify all six mechanical loading components applied to the composite. Of course, for each component only a single stress or strain may be specified, not both. This example simulates a complex thermomechanical loading history on a continuous fiber SiC/Ti-21S composite that involves application of stresses and strains in the x₁-x₂ plane. This loading profile might mimic a material point on the skin of an aerospace vehicle or engine housing. The 26´26 circular fiber approximation RUC architecture is employed. For more information on the code’s general mechanical loading option, see the MAC/GMC 4.0 Keywords Manual Section 4.

MAC/GMC Input File: example_4c.mac

MAC/GMC 4.0 Example 4c - RUC analysis general loading option

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=13 VF=0.25 R=1. F=1 M=2

*MECH

LOP=99

NPT=6 TI=0.,300.,310.,2310.,2320.,2620. MAG=0.,0.,0.01,0.01,0.,0. &

MODE=1,1,1,2,2

NPT=6 TI=0.,300.,310.,2310.,2320.,2620. MAG=0.,0.,0.005,0.005,0.,0. &

MODE=1,1,1,2,2

NPT=2 TI=0.,2620. MAG=0.,0. MODE=2

NPT=6 TI=0.,300.,310.,2310.,2320.,2620. MAG=0.,0.,0.0075,0.0075,0.,0. &

MODE=1,1,1,2,2

*THERM

NPT=6 TI=0.,300.,310.,2310.,2320.,2620. TEMP=23.,650.,650.,650.,650.,23.

*SOLVER

METHOD=1 NPT=6 TI=0.,300.,310.,2310.,2320.,2620. STP=1.,0.2,2.,1.,1.

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=4

NAME=example_4c X=1 Y=7

NAME=example_4c X=2 Y=8

NAME=example_4c X=6 Y=12

NAME=example_4c X=100 Y=101

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 26´26 circular fiber, rect. pack (ARCHID=13)

Fiber volume fraction: 0.25 (VF=0.25)

RUC aspect ratio: 1. (square pack) (R=1.)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: general loading (LOP=99)

Component #1 (e₁₁ or s₁₁)

Number of points: 6 (NPT=6)

Times (TI=) (sec.)	0.		300.		310.		2310.		2320.		2620.
Magnitudes (MAG=)	0.		0		0.01		0.01		0.		0.
Control (MODE=)		strain		strain		strain		stress		stress

Component #2 (e₂₂ or s₂₂)

Number of points: 6 (NPT=6)

Times (TI=) (sec.)	0.		300.		310.		2310.		2320.		2620.
Magnitudes (MAG=)	0.		0		0.005		0.005		0.		0.
Control (MODE=)		strain		strain		strain		stress		stress

Component #3 (e₃₃ or s₃₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		2620.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #4 (g₂₃ or s₂₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		2620.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #5 (g₁₃ or s₁₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		2620.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #6 (g₁₂ or s₁₂)

Number of points: 6 (NPT=6)

Times (TI=) (sec.)	0.		300.		310.		2310.		2320.		2620.
Magnitudes (MAG=)	0.		0		0.0075		0.0075		0.		0.
Control (MODE=)		strain		strain		strain		stress		stress

The simulated loading constitutes a state of plane stress in the x₁-x₂ plane, thus the stress associated with components 3 – 5 are kept at zero. The first loading segment involves the in-plane strain components being constrained (i.e., kept at zero) during which time a heat-up is specified in the thermal loading. Then, in-plane normal and shear strains are quickly applied and then held for 2000 sec. The control mode next switches from strain to stress for all three in-plane components, and the mechanical loading is reduced to zero in stress control. Finally, the composite is kept globally stress-free as the temperature is reduced during the final segment. This simulates a (fictitious) mission profile that might be encountered at a material point on the skin of an aerospace vehicle or engine as the vehicle warms up, takes off, flies, lands, and cools.

b) Thermal (*THERM) [KM_4]:

Number of points: 6 (NPT=6)

Time points: 0., 300., 310., 2310., 2320., 2620. sec.

(TI=0.,300.,310.,2310.,2320.,2620.)

Temperature points: 23., 650., 650., 650., 650., 23. °C

(TEMP=23.,650.,650.,650.,650.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 6 (NPT=6)

Time points: 0., 300., 310., 2310., 2320., 2620. sec.

(TI=0.,300.,310.,2310.,2320.,2620.)

Time step sizes: 1., 0.2, 2., 1., 1. sec. (STP=1.,0.2,2.,1.,1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_4]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_4]:

Frequency: 5 (FREQ=5)

Number of macro plots: 6 (MACRO=6)

Macro plot names: example_4c (NAME=example_4c)

Macro plot x-y quantities: , (X=1 Y=7)

, (X=2 Y=8)

, (X=6 Y=12)

temperature, time (X=100 Y=101)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 4.5 and Figure 4.6 show that during the first loading segment (0 – 300 sec.), while the temperature is increasing from 23 – 650 °C, no strain results and the normal stress components (s₁₁ and s₂₂) become compressive. This is due to the fact that the composite has been constrained against its natural thermal expansion during this heat-up. The shear stress component remains at zero because the composite does not experience shear thermal expansion (i.e., it is orthotropic). From 300 – 310 sec., the three strain components are quickly applied, and the stress components rise rapidly in response. Next, these three strain components are held constant for 2000 sec., during which time the stress components are free to relax. From 2310 – 2320 sec., the mechanical load, which was applied in strain control, is unloaded under stress control to zero for all three stress components. Finally, the temperature is decreased from 650 – 23 °C from 2320 – 2620 sec., during which time the stress components on the composite are held at zero. Therefore, the normal strain components decrease as the composite contracts while the shear strain remains constant. From Figure 4.6, it is clear that the composite experience permanent normal and shear strains at the completion of this thermomechanical loading history.

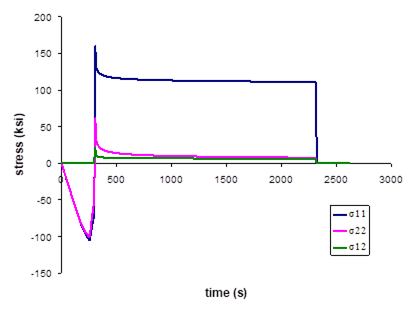
Figure 4.5 Example 4c: plot of the simulated stress vs. time history for a 0.25 fiber volume fraction SiC/Ti-21S composite.

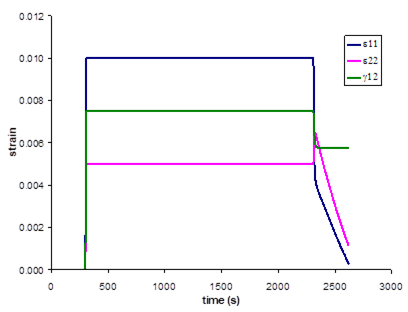
Figure 4.6 Example 4c: plot of the simulated strain vs. time history for a 0.25 fiber volume fraction SiC/Ti-21S composite.

Example 4d: Internal Loading Options for Laminate

This example problem demonstrates how to invoke the various internal mechanical loading options available for a laminate in MAC/GMC 4.0. In particular, the laminate analyzed is the identical quasi-isotropic 0.25 fiber volume fraction SiC/Ti-21S laminate presented in Example 3h. Because of the plane stress assumption inherent in lamination theory, only loading in the x-y plane of the laminate is permissible (where the z-direction is the through-thickness direction of the laminate, Figure 1.2). Further, loading in the form of midplane curvatures and moment resultants (in addition to midplane strains and force resultants) may be applied to the laminate using the internal loading option 4 – 6. Thus, the meaning of the various loading options is different in the case of a laminate as compared to the repeating unit cell analysis. For details, see Section 4 of the Keywords Manual. In the present example, the loading option is successively increased from 1 to 6 to apply the three midplane strain components and the three midplane curvatures in separate executions of the code.

MAC/GMC Input File: example_4d.mac

Lamination theory - Internal loading options for laminates

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*LAMINATE

NLY=7

LY=1 MOD=2 THK=0.125 ANG=90 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=2 MOD=2 THK=0.125 ANG=45 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=3 MOD=2 THK=0.125 ANG=0 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=4 MOD=2 THK=0.25 ANG=-45 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=5 MOD=2 THK=0.125 ANG=0 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=6 MOD=2 THK=0.125 ANG=45 ARCHID=6 R=1. VF=0.25 F=1 M=2

LY=7 MOD=2 THK=0.125 ANG=90 ARCHID=6 R=1. VF=0.25 F=1 M=2

*MECH

# -- Alter LOP from 1 - 6 to generate example problem results

LOP=1

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1.

*PRINT

NPL=6

*XYPLOT

FREQ=5

LAMINATE=6

NAME=example_4d_exx X=1 Y=10

NAME=example_4d_eyy X=2 Y=11

NAME=example_4d_exy X=6 Y=12

NAME=example_4d_kxx X=7 Y=13

NAME=example_4d_kyy X=8 Y=14

NAME=example_4d_kxy X=9 Y=15

MACRO=0

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 7 (NLY=7)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Aspect Ratio	Volume fraction	Fiber material	Matrix material
(LY=)	(MOD=2)	(THK=)	(ANG=)	(ARCHID=6)	(R=1.)	(VF=0.25)	(F=1)	(M=2)
1	GMC-2D	0.125	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
2	GMC-2D	0.125	45°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
3	GMC-2D	0.125	0°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
4	GMC-2D	0.25	-45°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
5	GMC-2D	0.125	0°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
6	GMC-2D	0.125	45°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
7	GMC-2D	0.125	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 1 – 6 (LOP=1 through LOP=6)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: midplane strain/curvature control (MODE=1)

F Note: To generate the results presented in this example, the loading option (LOP) must be changed from 1 to 6, successively.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of laminate plots: 6 (LAMINATE=6)

Laminate plot name: example_4d_exx (NAME=example_4d_exx)

example_4d_eyy (NAME=example_4d_eyy)

example_4d_exy (NAME=example_4d_exy)

example_4d_kxx (NAME=example_4d_kxx)

example_4d_kyy (NAME=example_4d_kyy)

example_4d_kxy (NAME=example_4d_kxy)

Laminate plot x-y quantitiies: , (X=1 Y=10)

, (X=2 Y=11)

, (X=6 Y=12)

, (X=7 Y=13)

, (X=8 Y=14)

, (X=9 Y=15)

Number of macro plots: 0 (MACRO=0)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 4.7 shows the response of the quasi-isotropic laminate to the three applied midplane strain components (LOP=1–3), whereas Figure 4.8 shows the laminate response to the three applied curvature components (LOP=4–6). It is clear from Figure 4.7 that the extensional behavior of the laminate is isotropic while Figure 4.8 shows that the bending behavior is anisotropic. The response of the laminate to the applied is stiffer than that to the applied because the outer plies of the laminate (which are farthest from the midplane and therefore contribute more to the bending stiffness) are oriented along the y-axis. It should also be noted that this laminate exhibits normal-shear coupling in its bending response (see Table 3.1).

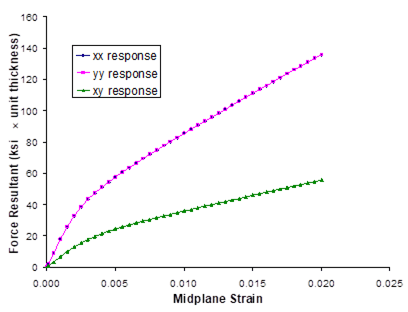
Figure 4.7 Example 4d: response of a 0.25 fiber volume fraction quasi-isotropic SiC/Ti-21S laminate to applied midplane strains at 650 °C.

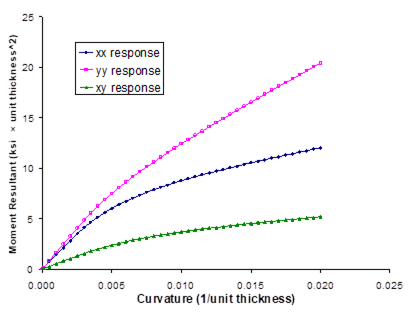
Figure 4.8 Example 4d: response of a 0.25 fiber volume fraction quasi-isotropic SiC/Ti-21S laminate to applied curvatures at 650 °C.

Example 4e: General loading Option for Laminates

This problem exercises the general loading option for a laminate. As in the previous example problem, the loading associated with the laminate involves force and moment resultants along with midplane strains and curvatures. Now, however, all six components applied to the laminate are specified via the LOP=99 loading option. In particular, an asymmetric elastic graphite/epoxy laminate is considered with temperature-dependent user-defined constituent properties. The laminate is subjected to a stress-free cool-down from 150 °C, which is intended to simulate the cure temperature. During the cool-down, the asymmetric laminate experiences bending (non-zero curvatures), and the subsequent mechanical loading eliminates this bending by returning the curvatures to zero. Thus, at the completion of the applied loading, the code has determined the moment resultants required to flatten the laminate after the thermally induced curvature.

MAC/GMC Input File: example_4e.mac

MAC/GMC 4.0 Example 4e - General loading option for laminates

*CONSTITUENTS

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=388.2E9,390.E9

ET=7.6E9,7.6E9

NUA=0.41,0.41

NUT=0.45,0.45

GA=14.9E9,15.1E9

ALPA=-0.68E-6,-0.45E-6

ALPT=9.74E-6,10.34E-6

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=3.45E9,3.10E9

ET=3.45E9,3.10E9

NUA=0.35,0.35

NUT=0.35,0.35

GA=1.278E9,1.148E9

ALPA=45.E-6,55.E-6

ALPT=45.E-6,55.E-6

*LAMINATE

NLY=4

LY=1 MOD=2 THK=0.25 ANG=90 ARCHID=6 R=1. VF=0.65 F=1 M=2

LY=2 MOD=2 THK=0.25 ANG=60 ARCHID=6 R=1. VF=0.65 F=1 M=2

LY=3 MOD=2 THK=0.25 ANG=-60 ARCHID=6 R=1. VF=0.65 F=1 M=2

LY=4 MOD=2 THK=0.25 ANG=0 ARCHID=6 R=1. VF=0.65 F=1 M=2

*MECH

LOP=99

NPT=3 TI=0.,1.,2. MAG=0.,0.,0. MODE=2,2

NPT=3 TI=0.,1.,2. MAG=0.,0.,0. MODE=2,1

*THERM

NPT=3 TI=0.,1.,2. TEMP=150.,23.,23.

*SOLVER

METHOD=1 NPT=3 TI=0.,2. STP=1.

*PRINT

NPL=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Constitutive models: Elastic (CMOD=6)

Materials: User-defined (Graphite) (MATID=U)

User-defined (Epoxy) (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 4.1

Table 4.1 Constituent material elastic properties for Example 4e.

	Temp (°C)	E_A (GPa)	E_T (GPa)	n_A	n_T	G_A (GPa)	a_A (10^-6/ °C)	a_T (10^-6/ °C)
Graphite	23.	388.2	7.6	0.41	0.45	14.9	-0.68	9.74
	150.	390.	7.6	0.41	0.45	15.1	-0.45	10.34
Epoxy	23.	3.45	3.45	0.35	0.35	1.278	45.	45.
	150.	3.10	3.10	0.35	0.35	1.148	55.	55.

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 4 (NLY=4)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Volume fraction	Aspect ratio	Fiber material	Matrix material
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(VF)	(R)	(F)	(M)
1	GMC-2D	0.25	90°	7´7 circle, rect. pack	0.65	1.	graphite	epoxy
2	GMC-2D	0.25	60°	7´7 circle, rect. pack	0.65	1.	graphite	epoxy
3	GMC-2D	0.25	-60°	7´7 circle, rect. pack	0.65	1.	graphite	epoxy
4	GMC-2D	0.25	0°	7´7 circle, rect. pack	0.65	1.	graphite	epoxy

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: general loading (LOP=99)

Component #1 ( or )

Number of points: 3 (NPT=3)

Times (TI=) (sec.)	0.		1.		2.
Magnitudes (MAG=)	0.		0.		0.
Control (MODE=)		force resultant		force resultant

Component #2 (or )

Number of points: 3 (NPT=3)

Times (TI=) (sec.)	0.		1.		2.
Magnitudes (MAG=)	0.		0.		0.
Control (MODE=)		force resultant		force resultant

Component #3 (or )

Number of points: 3 (NPT=3)

Times (TI=) (sec.)	0.		1.		2.
Magnitudes (MAG=)	0.		0.		0.
Control (MODE=)		force resultant		force resultant

Component #4 (or )

Number of points: 3 (NPT=3)

Times (TI=) ( sec.)	0.		1.		2.
Magnitudes (MAG=)	0.		0.		0.
Control (MODE=)		moment resultant		curvature

Component #5 (or )

Number of points: 3 (NPT=3)

Times (TI=) (sec.)	0.		1.		2.
Magnitudes (MAG=)	0.		0.		0.
Control (MODE=)		moment resultant		curvature

Component #6 (or )

Number of points: 3 (NPT=3)

Times (TI=) (sec.)	0.		1.		2.
Magnitudes (MAG=)	0.		0.		0.
Control (MODE=)		moment resultant		curvature

b) Thermal (*THERM) [KM_4]:

Number of points: 3 (NPT=3)

Time points: 0., 1., 2. sec. (TI=0.,1.,2.)

Temperature points: 150., 23., 23. °C (TEMP=150.,23.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 3 (NPT=3)

Time points: 0., 1., 2. sec. (TI=0.,1.,2.)

Time step sizes: 1., 1. sec. (STP=1.,1.)

F Note: Since this example problem is linearly elastic and the temperature-dependent constituent material properties are linear, the problem solution is independent of the number of time steps taken through the loading history. Therefore the minimum number of time steps (2) has been employed.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

The results below are taken from the MAC/GMC 4.0 output file for this example.

1 TIME: 1.0000D+00 TEMP: 2.3000D+01 TSTEP: 1.0000D+00

-------------------------------------------------------------------------------------------------------

FORCE(N), MOMENT(M): 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

STRAIN, CURVATURE: -1.2843D-03 -5.4894D-05 1.3757D-04 3.3269D-03 -4.3171D-04 -3.6875D-03

INELASTIC N, M: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

THERMAL N, M: -1.6159D+07 -1.0899D+07 -1.0789D-03 1.9726D+06 -1.9726D+06 -5.6944D+05

OUT-OF-PLANE STRAIN: -5.2503D-03 0.0000D+00 0.0000D+00

2 TIME: 2.0000D+00 TEMP: 2.3000D+01 TSTEP: 1.0000D+00

-------------------------------------------------------------------------------------------------------

FORCE(N), MOMENT(M): 0.0000D+00 0.0000D+00 0.0000D+00 -6.5415D+06 2.9887D+06 1.1301D+06

STRAIN, CURVATURE: -1.9617D-04 -4.3628D-05 -6.2573D-14 0.0000D+00 0.0000D+00 0.0000D+00

INELASTIC N, M: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

THERMAL N, M: -1.6159D+07 -1.0899D+07 -1.0789D-03 1.9726D+06 -1.9726D+06 -5.6944D+05

OUT-OF-PLANE STRAIN: -5.7715D-03 0.0000D+00 0.0000D+00

Upon completion of the stress-free cool down of the laminate (at time = 1. sec.), the laminate is bent (as indicated by the non-zero curvatures). Then, upon completion of the simulated mechanical loading (at time = 2. sec.), the laminate is no longer bent (as indicated by the zero curvatures). The moment resultants required to eliminate the laminate’s bending are: MPa ´ thickness², MPa ´ thickness², MPa ´ thickness², where thickness is the total thickness of the laminate (e.g., if the laminate were 1 mm thick, the required ). Recall that a moment resultant is a moment (with units force ´ length) per unit width of the laminate, yielding units of force.

Example 4f: RUC Yield Surface Analysis

This example problem demonstrates one of the more powerful capabilities of MAC/GMC 4.0, the generation of yield surfaces. A yield surface is defined as the locus of points in a stress space at which a specified “yield” condition is satisfied. For metals, a 0.1 % or 0.2 % permanent (inelastic) strain is often used as a yield condition, for example. However, this type of condition is based on uniaxial tension or compression, whereas, a yield surface, by definition is concerned with a multi-axial state of stress. A typical yield surface for a monolithic metal (aluminum, in this case) is shown in Figure 4.9. The “stress space” for this yield surface is the s₁₁-s₂₂ plane defined by the axes. The plotted yield surface then represents s₁₁-s₂₂ points that cause the metal to yield. Of course, this implies that some definition of what constitutes yielding has been employed. In Figure 4.9, yielding was defined as an equivalent plastic strain (EPS) of 0.001 (0.1 %), where and are the plastic strain components. Since EPS is a scalar value based on the multi-axial plastic strain state, it is suitable for use as a yield condition. The elliptical shape of the yield surface indicates that it is based on a von Mises type yield criterion. Indeed, the “yield surface” in Figure 4.9 was generated using the Bodner-Partom viscoplastic constitutive model, which employs a von Mises (J₂) type flow law. In viscoplasticity theory, no explicit yield condition exists that must be satisfied at all times. Therefore, a “yield” or “threshold” surface can be predicted for a viscoplastic material by specifying a particular criterion and checking for when it is satisfied during applied loading. This type of surface can then be generated for any material, regardless of the inelastic model formulation. However, some yield conditions are better suited than others for use in conjunction with particular inelastic constitutive models. For example, a surface generated from a rate-based criterion would not be appropriate for use in conjunction with a rate independent inelastic model such as incremental plasticity. It should be noted that, in its present form, the yield surface analysis implementation within MAC/GMC 4.0 is most relevant to composites and laminates that contain metals. However, the capabilities could also be applied to polymers and ceramics that exhibit inelastic deformation. For additional information on the code’s yield surface predictions, see Section 6 of the Theory Manual.

In order to generate a yield surface like that shown in Figure 4.9, MAC/GMC 4.0 applies combined mechanical loading in the given stress space. That is, loading is applied along a specific angle in the s₁₁-s₂₂ plane (for the present case) until the yield definition is encountered. Then, a new angle is chosen along which loading is applied until yield. This angle is referred to as the “probing angle”. When a sufficient number of angles have been probed, the locus of all the points at which yield occurred defines the yield surface. In MAC/GMC 4.0, the user specifies the increment to employ for the probing angle. The code then probes at angles from 0° to 360° using this angle increment. A small angle increment will generate a smoother yield surface, but requires more execution time as the code must execute for each probing angle.

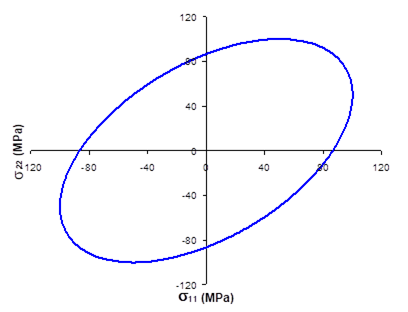
Figure 4.9 Yield surface for aluminum at room temperature based on EPS=0.001.

MAC/GMC Input File: example_4f.mac

MAC/GMC 4.0 Example 4f - RUC yield surface analysis

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=1 VF=0.25 F=1 M=2

#*THERM

# NPT=3 TI=0.,57600.,64800. TEMP=900.,23.,650.

#*SOLVER

# METHOD=1 NPT=3 TI=0.,57600.,64800. STP=40.,40.

*SURF

TMAX=400. STP=0.01 MMAX=0.04 MODE=1 TREF=650.

OPTION=1,2,3,4

ISPX=1 ISPY=2 ANGINC=5.

EPS=0.0001 DR=0.00025 ISR=0.00002 IP=0.001

*PRINT

NPL=1

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: Square fiber, square pack (ARCHID=1)

Fiber volume fraction: 0.25 (VF=0.25)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH): None

The loading for yield surface probing is controlled under *SURF. Any specified mechanical or thermal loading is interpreted as “preloading”, which is applied prior to beginning the yield surface probing. This allows the user to incorporate a certain stress/strain state into the composite prior to determination of the yield surface.

b) Thermal (*THERM) [KM_4]: (case with residual stresses only)

Number of points: 3 (NPT=3)

Time points: 0., 57600., 64800. sec. (TI=0.,57600.,64800.)

Temperature points: 900., 23., 650. (TEMP=900.,23.,650.)

c) Time integration (*SOLVER) [KM_4]: (case with residual stresses only)

Time integration method: Forward Euler (METHOD=1)

Number of points: 3 (NPT=3)

Time points: 0., 57600., 64800. sec. (TI=0.,57600.,64800.)

Time step size: 40., 40. sec. (STP=40.,40.)

F Note: As with the mechanical loading, the thermal loading in yield surface analysis is interpreted by the code as “preloading”. Thus, the thermal loading specified allows residual stresses to be included in the composite prior to the yield surface probing. To execute this example problem without residual stresses, the *THERM and *SOLVER keyword data should be commented as shown above. To execute with residual stresses, these should be uncommented.

d) Yield surface generation (*SURF) [KM_4]:

Maximum probing time: 400. sec. (TMAX=400.)

Probing time step size: 0.01 sec. (STP=0.01)

Maximum probing load: 0.04 (MMAX=0.04)

Probing mode: strain control (MODE=1)

Reference temperature: 650. °C (TREF=650.)

Yield surface options: Generate global data (1) (OPTION=1,2,3,4)

Generate 1st subcell data (2)

Generate all subcells data (3)

Generate local subcell data (4)

Stress space x-axis: s₁₁ (ISPX=1)

Stress space y-axis: s₂₂ (ISPY=2)

Probe angle increment: 5.° (ANGINC=5)

Quantities defining yield: Equivalent plastic strain = 0.0001 (EPS=0.0001)

Dissipation rate = 0.00025 (DR=0.00025)

Inelastic strain rate = 0.00002 (ISR=0.00002)

Inelastic power = 0.001 (IP=0.001)

The mechanical loading for the yield surface probing is specified under *SURF in the form of a maximum time (TMAX), time step (STP), maximum load (MMAX), and mode (MODE). The yield surface mechanical loading is unique from that specified under *MECH in that only one segment may be employed. If, at a particular probing angle, the maximum time is reached before all yield criteria are satisfied, a warning is written to the output file, and the probing proceeds to the next angle. Thus a large maximum probing load and maximum probing time should be employed. In addition, the time step size needs to be reasonably small such that the exact point of yielding can be captured. The rate of the applied loading is determined from the maximum time and maximum load data. This rate is interpreted as a J₂ (stress) or J₂’ (strain) quantity. This allows the loading rate to be consistent as the probing angle changes. If thermal preloading is not specified with *THERM, then TREF must be specified under *SURF in order to indicate the temperature at which the yield surface is determined. If thermal preloading is specified, this TREF is ignored and the ending temperature from the thermal preloading is employed.

The yield surface option (*SURF) generates up to four ASCII files (for the case of RUC analysis) that contain the yield surface data. These are: surf_global.dat, surf_1st.dat, surf_all.dat, and surf_local.dat. surf_global.dat contains the global yield surface data for each type of yield surface (i.e., EPS, DR, ISR, and IP), surf_1st.dat contains the yield surface data based on first subcell yield for each type of yield surface, surf_all.dat contains the yield surface data based on the requirement that all subcells (that can yield) yield for each type of yield surface, and surf_local.dat contains the yield surface data for each individual subcell for each type of yield surface.

The stress space is defined by ISPX and ISPY. In this example, the s₁₁-s₂₂ stress space is specified, which indicates that loading will be applied in the x₁-direction (along the fiber direction) and the x₂-direction (transverse to the fiber direction). Additional options are available using ISPX and ISPY, including applying additional loading components that are slaves to (i.e., equal to) the primary stress space loading components. These options are described in the MAC/GMC 4.0 Keywords Manual Section 4.

The yield surface probing occurs along angles in the stress space determined by the specified probe angle increment (ANGINC). That is, for example, when probing at an angle of 5° in the s₁₁-s₂₂ stress space, the code applies loading such that s₁₁/s₂₂ = tan(5°). Upon fulfillment of all yield criteria (or upon reaching the end of the specified maximum time), the code proceeds to the next probing angle. If preloading is specified, the code begins each probing angle not at a zero stress-strain state, but rather at the stress-strain state that existed at the end of the preload. A smaller probe angle increment results in a smoother predicted yield surface, but will increase the execution time. For additional information on the MAC/GMC 4.0 yield surface capabilities and procedures, see the MAC/GMC 4.0 Keywords Manual Section 4.

The particular yield values chosen in this example problem are arbitrary. It is possible to see when yielding occurs at a particular probe angle by generating an x-y plot and obtaining a particular yield point from the notification written to the output file. The yield values can the be adjusted as desired to make the yield prediction more or less conservative.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 0 (NPL=0)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

Some of the yield surface data results from this example are plotted in Figure 4.10 – Figure 4.15. All yield surface data generated have not been plotted as this example generates data for six yield surfaces of each type (i.e., EPS, DR, ISR, and IP) for both the cases with and without residual. Figure 4.10 shows the global yield surfaces for the case without residual stresses. The term “global” refers to the fact that the composite or RUC level stresses, strains, and rates have been employed to determine when yielding occurs. All four yield surfaces in Figure 4.10 are biased (i.e., elongated) along the s₁₁-axis due to the presence of the continuous fibers, which elevate the yield stress, in the x₁-direction. Based on the yield values specified in the input files (which are somewhat arbitrary), the composite tends to yield first with respect to the dissipation rate (DR), followed by the inelastic power (IP), the inelastic strain rate (ISR), and finally by the equivalent plastic strain (EPS). The four yield surfaces are similar in shape and all are centered about the stress space origin, with the ISR surface being the most elongated.

Figure 4.11 shows the same four yield surfaces for the case in which residual stresses have been incorporated. Qualitatively, these yield surfaces are similar to their counterparts from Figure 4.10. The major difference is that the yield surfaces are shifted to the left due to the compressive residual stresses in the matrix.

Figure 4.12 presents all six equivalent plastic strain (EPS) yield surfaces from the case in which residual stresses were not included. The global yield surface is the same as that plotted in Figure 4.10 (labeled “EPS Global”). Also plotted are the yield surfaces associated with the three individual matrix subcells (b,g = 1,2; 2,1; and 2,2), see Figure 4.16. Because the 2,2 subcell is farthest from the fiber, this subcell has a significantly larger yield surface than the 1,2 and 2,1 subcells. The 1,1 subcell is occupied by the elastic fiber and thus does not have a yield surface. The first subcell yield surface generated by MAC/GMC 4.0 traces the intersection of the individual subcell yield surfaces. Conversely the yield surface generated by requiring all subcells to yield traces the union of the individual subcell yield surfaces (which, in Figure 4.12, coincides with the subcell 2,2 yield surface).

The counterpart to Figure 4.12 is Figure 4.13, which contains the same six yield surfaces for the case including residual stresses. Now, the subcell 2,2 yield surface intersects the subcell 1,2 and 2,1 yield surfaces, giving rise to irregularly shaped first subcell and all subcells yield surfaces in the vicinity of the tensile s₁₁-axis. This irregularity of the all subcells EPS yield surface can be seen more clearly in Figure 4.14, which directly compares EPS yield surfaces for the cases with and without residual stresses. Further, this figure shows that residual stresses have translated the yield surfaces slightly in the direction of the tensile s₂₂-axis in addition to the compressive s₁₁ translation mentioned previously. Finally, Figure 4.15 compares inelastic strain rate (ISR) yield surfaces for the cases with and without residual stresses.

Figure 4.10 Global (RUC) yield surfaces for 0.25 fiber volume fraction SiC/Ti-21S at 650 °C with no residual stresses.

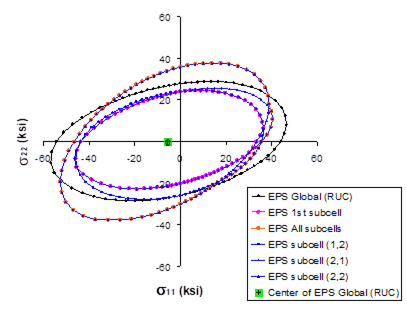
Figure 4.11 Global (RUC) yield surfaces for 0.25 fiber volume fraction SiC/Ti-21S at 650 °C with residual stresses.

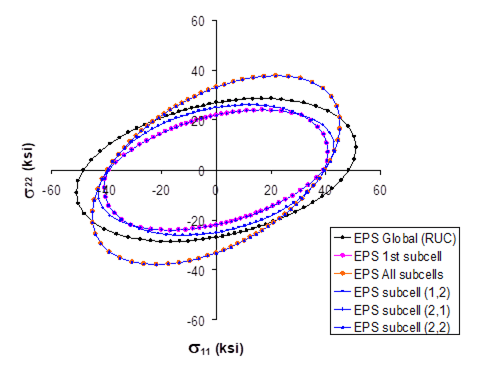
Figure 4.12 Local and global equivalent plastic strain (EPS) yield surfaces for 0.25 fiber volume fraction SiC/Ti-21S at 650 °C with no residual stresses.

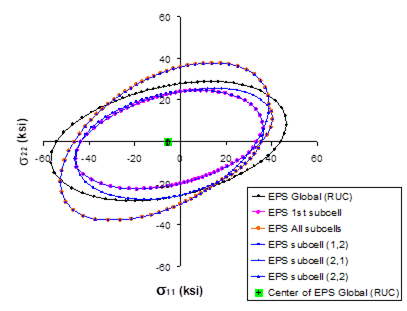
Figure 4.13 Local and global equivalent plastic strain (EPS) yield surfaces for 0.25 fiber volume fraction SiC/Ti-21S at 650 °C with residual stresses.

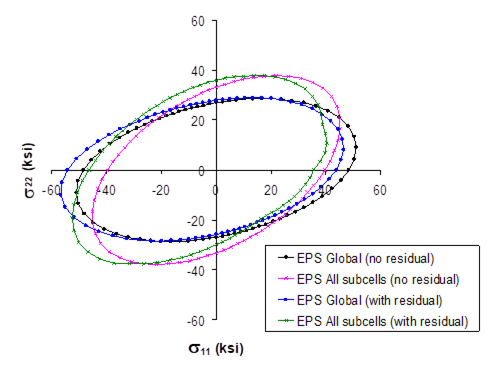
Figure 4.14 Comparison of equivalent plastic strain (EPS) yield surfaces for 0.25 fiber volume fraction SiC/Ti-21S at 650 °C with and without residual stresses.

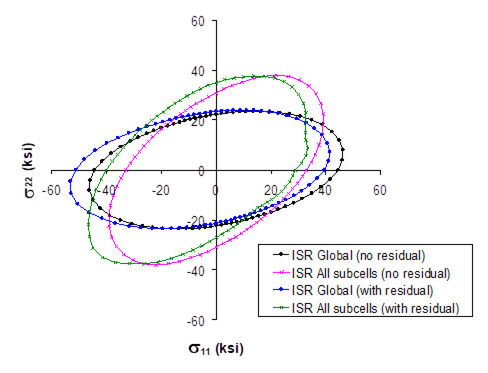
Figure 4.15 Comparison of inelastic strain rate (ISR) yield surfaces for 0.25 fiber volume fraction SiC/Ti-21S at 650 °C with and without residual stresses.

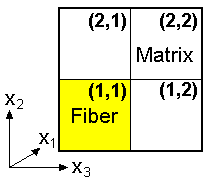
Figure 4.16 2´2 RUC representing the 0.25 fiber volume fraction SiC/Ti-21S composite in Example 4f. The subcell indices (b,g) are indicated.

Example 4g: Laminate Yield Surface Analysis

This example problem illustrates the laminate yield surface capabilities within MAC/GMC 4.0. In particular, a cross-ply 0.25 fiber volume fraction SiC/Ti-21S laminate, with each layer represented by the 7´7 circular fiber cross-section approximation RUC architecture, is examined. For the RUC yield surface analyses presented in Example 4f, the stress space was defined by global stress quantities. For laminate yield surface analysis, the global loading quantities are force resultants, which define the force resultant space for the yield surface. In accordance with the plane stress formulation of lamination theory, only in-plane yield surfaces may be generated for laminates. Yield surfaces that involve bending of the laminate may not be generated. Additional options are available for laminate yield surface analysis as yield surfaces can be generated on the level of the laminate, the ply, and the individual subcells that constitute each ply.

MAC/GMC Input File: example_4g.mac

MAC/GMC 4.0 Example 4f - Laminate yield surface analysis

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*LAMINATE

NLY=3

LY=1 MOD=2 THK=0.25 ANG=0 ARCHID=6 VF=0.25 R=1. F=1 M=2

LY=2 MOD=2 THK=0.50 ANG=90 ARCHID=6 VF=0.25 R=1. F=1 M=2

LY=3 MOD=2 THK=0.25 ANG=0 ARCHID=6 VF=0.25 R=1. F=1 M=2

*SURF

TMAX=400. STP=0.05 MMAX=0.04 MODE=1 TREF=650.

OPTION=1,2,3,4,5,6,7

ISPX=1 ISPY=2 ANGINC=5.

EPS=0.0001 DR=0.00025 ISR=0.00002 IP=0.001

*PRINT

NPL=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 3 (NLY=3)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Aspect Ratio	Volume fraction	Fiber material	Matrix material
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(R)	(VF)	(F)	(M)
1	GMC-2D	0.25	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
2	GMC-2D	0.50	0°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S
3	GMC-2D	0.25	90°	7´7 circle, rect. pack	1.	0.25	SiC	Ti-21S

4) Loading:

a) Mechanical (*MECH) [KM_4]: no mechanical preloading

b) Thermal (*THERM) [KM_4]: no thermal preloading

c) Time integration (*SOLVER) [KM_4]: no preloading

d) Yield surface generation (*SURF) [KM_4]:

Maximum probing time: 400. sec. (TMAX=400.)

Probing time step size: 0.05 sec. (STP=0.05)

Maximum probing load: 0.04 (MMAX=0.04)

Probing mode: strain control (MODE=1)

Reference temperature: 650. °C (TREF=650.)

Yield surface options: Generate global (laminate) data (1) (OPTION=1,2,3,4,5,6,7)

Generate 1st ply data (2)

Generate all plies data (3)

Generate data for each ply (4)

Generate 1st subcell data (5)

Generate all subcells data (6)

Generate local subcell data (7)

Force resultant space x-axis: N_xx (ISPX=1)

Force resultant space y-axis: N_yy (ISPY=2)

Probe angle increment: 5.° (ANGINC=5)

Quantities defining yield: Equivalent plastic strain = 0.0001 (EPS=0.0001)

Dissipation rate = 0.00025 (DR=0.00025)

Inelastic strain rate = 0.00002 (ISR=0.00002)

Inelastic power = 0.001 (IP=0.001)

For laminate analysis, the yield surface option (*SURF) generates up to seven ASCII files that contain the yield surface data. surf_global.dat contains the global (i.e., laminate level) yield surface data for each type of yield surface (i.e., EPS, DR, ISR, and IP), surf_1st_ply.dat contains the yield surface data based on first ply yield for each type of yield surface, surf_all_plies.dat contains the yield surface data based on the requirement that all plies (that can yield) yield for each type of yield surface, surf_plies.dat contains the yield surface data for each individual ply for each type of yield surface, surf_1st.dat contains the yield surface data based on first subcell yield for each type of yield surface, surf_all.dat contains the yield surface data based on the requirement that all subcells (that can yield) yield for each type of yield surface, and surf_local.dat contains the yield surface data for each individual subcell for each type of yield surface. Thus, laminate analysis adds an additional level in the yield surface data hierarchy.

F Note: In general, the quantities necessary for determining global (laminate level) yield are not present in standard lamination theory. That is, for instance, lamination theory calculates laminate level inelastic force resultants rather than laminate level inelastic strains, which are needed for evaluation of yielding. Therefore, for use within the yield calculations, MAC/GMC 4.0 determines effective laminate level quantities when appropriate.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 0 (NPL=0)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

Figure 4.17 presents the four global (laminate level) yield surfaces generated in this example. Because a [0°/90°]_s laminate is simulated and residual stresses are not included, a particular yield surface crosses each axis at the same force resultant magnitude. In addition, the yield surfaces are less elongated than those that correspond to the continuous SiC/Ti-21S composite in Figure 4.10.

Figure 4.18 shows additional equivalent plastic strain (EPS) yield surfaces. The yield surfaces generated based on yield of the 0° ply and the 90° ply intersect (much like the subcell-based yield surfaces intersect in Figure 4.12). The yield surface based on first ply yield traces the intersection of the individual ply curves, while the yield surface based on requiring yield of all plies traces the union. Also plotted in Figure 4.18 is the EPS yield surface based on first subcell yield. This is the smallest surface plotted because it is based on yielding of any subcell in any of the plies. Conversely, the yield surface based on requiring yielding of all subcells in all plies tends to be large. At certain locations, however, the global laminate yield surface is larger than the all subcells yield surface because the global yield surface is based on volume-average quantities, which include the 0.25 volume fraction fiber. Thus, while the subcell-based yield surfaces relate to the matrix material occupying the particular subcell, the laminate (and ply) level yield surfaces have averaged in the effect of the elastic fiber (which contributes zero plastic strain).

Figure 4.19 shows the yield surfaces associated with each of the individual subcells within each layer. The first subcell yield surface and the all subcells yield surface automatically select the intersection and union, respectively, of the individual subcell yield surfaces.

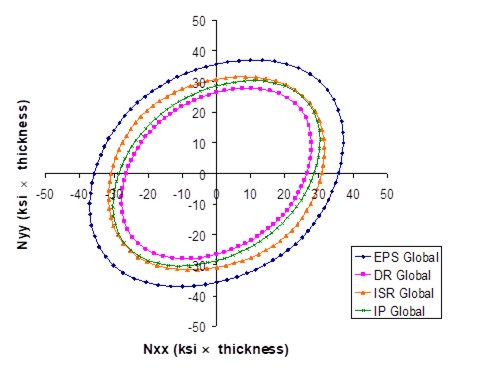
Figure 4.17 Global (laminate) yield surfaces for a 0.25 fiber volume fraction [0°/90°]_s SiC/Ti-21S laminate.

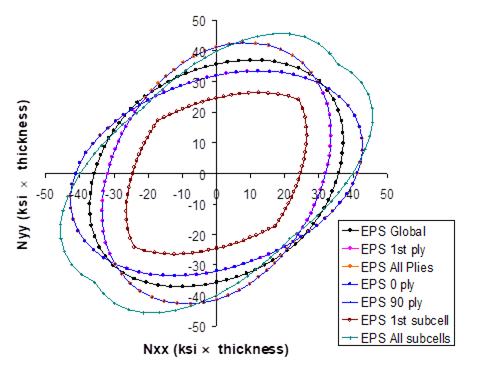
Figure 4.18 Equivalent plastic strain (EPS) yield surfaces for a 0.25 fiber volume fraction [0°/90°]_s SiC/Ti-21S laminate.

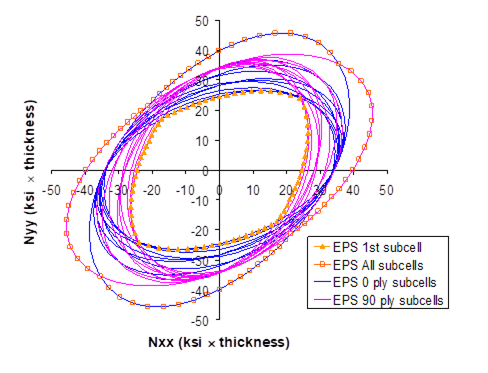
Figure 4.19 Subcell-based equivalent plastic strain (EPS) yield surfaces for a 0.25 fiber volume fraction [0°/90°]_s SiC/Ti-21S laminate.

Example 4h: Predictor-Corrector Time Integration

This example problem demonstrates the use of the predictor-corrector time integration method within MAC/GMC 4.0, which employs a self-adaptive time stepping scheme. This method is based on a fourth-order Runge-Kutta starter, an Adams-Bashforth four-step predictor, and an Adams-Moulton four-step corrector. Instead of specifying an explicit time step size (as in the forward Euler time integration method), the user specifies an acceptable level of error between the predicted and corrected values (for each local and global variable). The predictor-corrector integration algorithm then automatically adjusts the time step size in order to take the largest possible time step while ensuring that the error remains below the error tolerance. For additional information see Section 7.2 of the Theory Manual. The present problem considers a unidirectional 0.35 fiber volume fraction SiC/Ti-21S composite as represented by the 7´7 circular fiber cross-section approximation RUC architecture. A stress-free cool-down is first applied to incorporate residual stresses (see Example 4b), followed by cyclic mechanical loading.

MAC/GMC Input File: example_4h.mac

MAC/GMC 4.0 Example 4h - Predictor-corrector time integration method

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=6 VF=0.35 R=1. F=1 M=2

*MECH

LOP=2 REFTIME=57600.

NPT=8 TI=0.,57600.,57630.,57650.,57690.,57710.,57770.,57790. &

MAG=0.,0.,0.015,0.,0.02,0.,0.03,0. MODE=2,1,2,1,2,1,2

*THERM

NPT=3 TI=0.,57600.,57790. TEMP=900.,23.,23.

*SOLVER

METHOD=2 ISTM=0.001 ISTT=0.1 ERR=0.001 MINSTEP=0.00001

*PRINT

NPL=3

*XYPLOT

FREQ=5

MACRO=3

NAME=example_4h X=2 Y=8

NAME=example_4h_th1 X=100 Y=1

NAME=example_4h_th2 X=100 Y=2

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 7´7 circle approx., rect. pack (ARCHID=6)

Fiber volume fraction: 0.35 (VF=0.35)

RUC aspect ratio: 1. (square pack) (R=1.)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 2 (LOP=2)

Strain reference time: 57600. sec. (REFTIME=57600.)

Number of points: 8 (NPT=8)

Times (TI=) (sec.)	0.		57600.		57630.		57650.		57690.		57710.		57770.		57790.
Magnitudes (MAG=)	0.		0		0.015		0.0		0.02		0.		0.03		0.
Control (MODE=)		stress		strain		stress		strain		stress		strain		stress

In this example, the mechanical loading is applied in strain control and unloaded in stress control. This allows the stress to be precisely controlled so that it returns to zero after each cycle.

b) Thermal (*THERM) [KM_4]:

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57790. sec. (TI=0.,57600.,57790.)

Temperature points: 900., 23., 23. (TEMP=900.,23.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Predictor-corrector (METHOD=2)

Initial mech. time step: 0.001 sec. (ISTM=0.001)

Initial thermal time step: 0.1 sec. (ISTT=0.1)

Error tolerance: 0.001 (ERR=0.001)

Minimum time step size: 0.00001 sec. (MINSTEP=0.00001)

The initial mechanical (ISTM) and thermal (ISTT) time steps are used to start the time integration with the fourth-order Runge-Kutta method. The error tolerance (ERR) is maximum allowable fractional difference between a predicted and corrected value for any local or global variable. The minimum time step size (MINSTEP) limits how small the time step can become, regardless of the predicted and corrected variable values. As the results of this example indicate, the above values for these terms work well in the present case, but they can be case dependent. Users are thus encouraged to employ values for the terms based on experience with their own particular problems. For additional information of the predictor-corrector, see the MAC/GMC 4.0 Keywords Manual Section 4 and the Theory Manual Section 7.2.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 3 (NPL=3)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 3 (MACRO=3)

Macro plot name: example_4h (NAME=example_4h)

example_4h_th1 (NAME=example_4h_th1)

example_4h_th2 (NAME=example_4h_th2)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

temperature, ε₁₁ (X=100 Y=1)

temperature, ε₂₂ (X=100 Y=2)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 4.20 shows the longitudinal and transverse strain induced in the SiC/Ti-21S composite as it is cooled from 900 °C to room temperature. The predictor corrector begins with a small initial time step, which soon increases as the temperature is dropping. At approximately 700 °C, the composite begins to experience inelastic deformation, causing the time step to become very small. At lower temperatures, the inelastic strain rate becomes smaller, and the time step is increased.

Figure 4.21 shows the subsequent transverse cyclic tensile response of the composite. Again, as the mechanical loading begins, the time step is small. The composite behaves as initially elastic, thus the time step increases rapidly. As the composite begins to yield, the time step decreases, and subsequently increases several times. This is due to yielding of the individual subcells within the composite. Once a given subcell yields and begins to flow at a predictable rate, the predictor-corrector can increase the time step until another subcell starts to yield. The unloading and reloading behavior of the composite is mainly elastic in nature, so the time step increases for these segments of the stress-strain response. When the composite begins to yield for each cycle, the time step decreases once more.

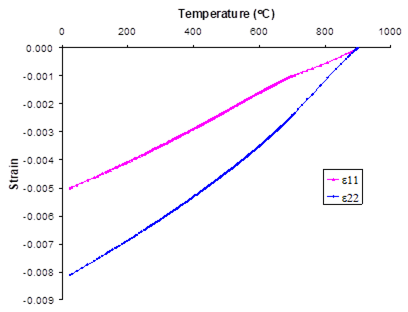
Figure 4.20 Example 4h: Stress-free cool-down response of 0.35 fiber volume fraction SiC/Ti-21S generated using the predictor-corrector time integration scheme.

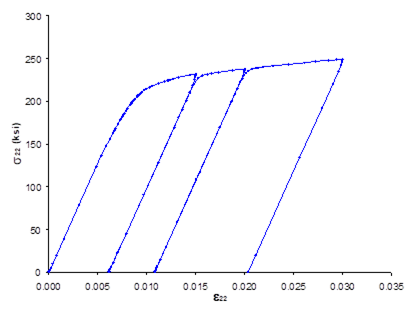
Figure 4.21 Example 4h: Cyclic transverse tensile response of 0.35 fiber volume fraction SiC/Ti-21S at room temperature generated using the predictor-corrector time integration scheme.

Section 5 : Damage and Failure

In this section, example problems are presented that invoke the failure and damage analysis capabilities resident in MAC/GMC 4.0. The code is capable of performing an array of failure and damage simulations with varying levels of complexity. The six keywords used to specify the failure and damage analysis input are:

*ALLOWABLES

*FAILURE_SUBCELL

*FAILURE_CELL

*DAMAGE

*DEBOND

*CURTIN

The simplest (non-conservative) type of failure analysis is estimation of composite elastic allowable stress and strain values from stress and strain allowable data of the constituent materials. Calculation of these estimated allowables is efficient since they do not require application of any load history and are based solely on the linear elastic properties of the composite constituents. Static failure analysis, on the other hand, is inherently linked to applied loading histories in that the analysis constantly checks user specified failure criteria, on either the RUC or subcell level, during application of the simulated loading. Thus, if inelastic deformation or thermal strains are present in the composite, they will affect the static failure analysis results.

Continuum fatigue damage analysis is distinct from allowables estimation and static failure analysis in that it involves simulation of the effects of cyclic loading. MAC/GMC 4.0 includes two fatigue damage models, one that involves stiffness degradation due to the cyclic loading (suitable for simulating the matrix phase), and one that involves strength degradation due to the cyclic loading (suitable for simulating the fiber phase). Fiber-matrix debonding and longitudinal fiber breakage are two additional failure/damage phenomena that can be modeled using MAC/GMC 4.0.

All of the failure and damage capabilities of MAC/GMC 4.0 can be attributed to the ability of the generalized method of cells to localize the multi-axial state of stress and strain on a composite or laminate to stresses and strains on the material occupying each subcell. This local state of stress and strain can then be employed within a particular failure or damage model to determine the state of local failure or damage. Then, GMC homogenizes the local results so that the effect of the local failure or damage of a given constituent on the overall composite or laminate behavior can be determined.

Example 5a: Composite Allowables Calculation

MAC/GMC 4.0 includes the ability to determine elastic stress and strain allowables for a composite based on the stress and strain allowables for the constituents. The calculations are based on pure elastic concentration analyses in which, through GMC, the global stress or strain is determined that leads to the stress or strain allowable being reached locally. Because the calculated allowables are based on linear elastic calculations, include no residual stresses or damage, and have not been validated experimentally, they should be thought of as estimated values only. The user is strongly cautioned that the estimated allowables should not be interpreted as “design allowables” that are, by definition, certified via extensive comparison with experimental data. The estimated allowables calculated by the code should also be considered non-conservative.

This problem considers a continuous 0.60 fiber volume fraction graphite/epoxy composite represented by the refined 26´26 circular fiber cross-section approximation RUC architecture. No thermal or mechanical loading is applied as the problem is only concerned with the determination of the allowables.

MAC/GMC Input File: example_5a.mac

MAC/GMC 4.0 Example 5a - RUC allowables calculation

*CONSTITUENTS

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=388.2E3,390.E3

ET=7.6E3,7.6E3

NUA=0.41,0.41

NUT=0.45,0.45

GA=14.9E3,15.1E3

ALPA=-0.68E-6,-0.45E-6

ALPT=9.74E-6,10.34E-6

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=3.45E3,3.10E3

ET=3.45E3,3.10E3

NUA=0.35,0.35

NUT=0.35,0.35

GA=1.278E3,1.148E3

ALPA=45.E-6,55.E-6

ALPT=45.E-6,55.E-6

*RUC

MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

*ALLOWABLES

NMAT=2

MAT=1

S11=3500. S22=91.2 S33=91.2 S23=31.4 S13=134. S12=134. COMPR=SAM

E11=0.009 E22=0.012 E33=0.012 E23=0.012 E13=0.009 E12=0.009 COMPR=SAM

MAT=2

S11=80. S22=80. S33=80. S23=40. S13=40. S12=40. COMPR=SAM

E11=0.023 E22=0.023 E33=0.023 E23=0.031 E13=0.031 E12=0.031 COMPR=SAM

*PRINT

NPL=-1

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Constitutive models: Elastic (CMOD=6)

Materials: User-defined (Graphite) (MATID=U)

User-defined (Epoxy) (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 4.1

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 26´26 circular fiber approx., rect. pack (ARCHID=13)

Fiber volume fraction: 0.60 (VF=0.60)

Unit cell aspect ratio: 1.0 (square pack) (R=1.0)

Material assignment: graphite fiber (F=1)

epoxy matrix (M=2)

4) Loading: None

5) Damage and Failure:

a) Stress and strain allowables estimation (*ALLOWABLES) [KM_5]:

Number of materials: 2 (NMAT=2)

Fiber stress allowables: s₁₁ = 3500. MPa (S11=3500.)

(MAT=1) s₂₂ = 91.2 MPa (S22=91.2)

s₃₃ = 91.2 MPa (S33=91.2)

s₂₃ = 31.4 MPa (S23=31.4)

s₁₃ = 134. MPa (S13=134.)

s₁₂ = 134. MPa (S12=134.)

Fiber strain allowables: e₁₁ = 0.009 (E11=0.009)

e₂₂ = 0.012 (E22=0.012)

e₃₃ = 0.012 (E33=0.012)

g₂₃ = 0.012 (E23=0.012)

g₁₃ = 0.009 (E13=0.009)

g₁₂ = 0.009 (E12=0.009)

Fiber compression flag: Compression same as tension (COMPR=SAM)

Matrix stress allowables: s₁₁ = 80. MPa (S11=80.)

(MAT=2) s₂₂ = 80. MPa (S22=80.)

s₃₃ = 80. MPa (S33=80.)

s₂₃ = 40. MPa (S23=40.)

s₁₃ = 40. MPa (S13=40.)

s₁₂ = 40. MPa (S12=40.)

Matrix strain allowables: e₁₁ = 0.023 (E11=0.023)

e₂₂ = 0.023 (E22=0.023)

e₃₃ = 0.023 (E33=0.023)

g₂₃ = 0.031 (E23=0.031)

g₁₃ = 0.031 (E13=0.031)

g₁₂ = 0.031 (E12=0.031)

Matrix compression flag: Compression same as tension (COMPR=SAM)

As shown, stress and strain allowables may be specified for one or more materials within the composites. If allowables are specified for some, but not all constituent materials, the materials for which allowables were not specified will be skipped (i.e., not considered in the allowables calculation). Each of the six stress and strain allowable components may be specified for each material. If a particular component is not specified for a particular material, the calculation will skip that component for that material. A compression flag (COMPR) must also be specified for each material. This indicates how compression is handled for that material. COMPR=SAM indicates that the normal compressive allowables are of the same magnitude as the normal tensile allowables, COMPR=OFF indicates that code should not perform compressive allowables calculations, and COMPR=DIF indicates that the normal compressive allowables are of different magnitude than the normal tensile allowables. For this latter case, three compressive allowables may be specified as: SC11= SC22= SC33= and EC11= EC22= EC33= . The actual constituent allowable values employed in this problem are fictitious. For more information on the estimated allowables calculations, see the MAC/GMC 4.0 Keywords Manual Section 5.

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: -1 (effective properties only) (NPL=-1)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

Results from the estimated allowables calculations are written to the MAC/GMC 4.0 output file:

* ESTIMATED ELASTIC STRESS ALLOWABLES *

*************************************************************

** CAUTION - These allowables have not been validated and **

** are based only on linear elastic calculations **

*************************************************************

--- 1st Subcell --- --- Avg Material --- - All Subcells -

ALLOWABLE CRITICAL ALLOWABLE CRITICAL ALLOWABLE

COMP STRESS SUBCELL STRESS MATERIAL STRESS

---- ---------- -------- ---------- -------- ----------

1 0.2112E+04 325 0.2112E+04 1 0.5599E+04

2 0.6808E+02 13 0.8416E+02 1 0.1199E+03

3 0.6808E+02 339 0.8416E+02 1 0.1199E+03

4 0.3140E+02 39 0.3140E+02 1 0.4000E+02

5 0.2489E+02 313 0.5764E+02 2 0.3179E+03

6 0.2489E+02 13 0.5764E+02 2 0.3179E+03

---- ---------- --------- ---------- -------- ----------

1 -0.2112E+04 325 -0.2112E+04 1 -0.5599E+04

2 -0.6808E+02 13 -0.8416E+02 1 -0.1199E+03

3 -0.6808E+02 339 -0.8416E+02 1 -0.1199E+03

* ESTIMATED ELASTIC STRAIN ALLOWABLES *

*************************************************************

** CAUTION - These allowables have not been validated and **

** are based only on linear elastic calculations **

*************************************************************

--- 1st Subcell --- --- Avg Material --- - All Subcells -

ALLOWABLE CRITICAL ALLOWABLE CRITICAL ALLOWABLE

COMP STRAIN SUBCELL STRAIN MATERIAL STRAIN

---- ---------- -------- ---------- -------- ----------

1 0.9000E-02 39 0.9000E-02 1 0.2300E-01

2 0.1283E-01 325 0.1417E-01 1 0.2770E-01

3 0.1283E-01 351 0.1417E-01 1 0.2770E-01

4 0.1704E-01 39 0.1704E-01 1 0.2147E-01

5 0.6549E-02 313 0.1517E-01 2 0.8454E-01

6 0.6549E-02 13 0.1517E-01 2 0.8454E-01

---- ---------- --------- ---------- -------- ----------

1 -0.9000E-02 39 -0.9000E-02 1 -0.2300E-01

2 -0.1283E-01 325 -0.1417E-01 1 -0.2770E-01

3 -0.1283E-01 351 -0.1417E-01 1 -0.2770E-01

NOTE: 1st subcell --> based on 1st subcell reaching specified constituent allowable

Avg material --> based on 1st material whose avg stress/strain reaches allowable

All subcells --> based on all subcells reaching specified constituent allowable

Three sets of results are generated for the estimated composite stress and strain allowables. “1^st Subcell” allowables are determined based on any subcell within the RUC reaching the specified allowable value for the material within the subcell. This is the most conservative estimated allowable as, due to stress concentrations, certain subcells may locally reach the allowable at a low global stress or strain level. An intermediate “Avg Material” allowable is determined by finding the global stress or strain at which the average stress or strain for each constituent material reaches the specified allowable for that material. Finally, the most liberal (non-conservative) allowable estimate (“All Subcells”) is determined by requiring every subcell within the RUC to reach its allowable stress or strain. For the present example, the composite compressive results are identical (in magnitude) to the tensile results as, for both constituent materials, the compressive allowables are the same as the tensile allowables.

The results from this example problem are presented in graphical form in Figure 5.1 and Figure 5.2. The independent estimated allowable components have been normalized by the corresponding specified fiber allowable values. For comparison, the normalized values specified for the matrix material have been plotted as well. Figure 5.1 and Figure 5.2 clearly show that the average material allowables are bounded by the 1^st subcell and all subcells allowables. Further, in all cases, the composite average material allowable falls in between the specified matrix and fiber allowables. This is not the case for the 1^st subcell allowable, which falls below both constituent allowables for s₂₂, s₁₂, and g₁₂. Likewise, the all subcells allowable is greater than the allowable for both constituents for s₁₁, s₂₂, s₁₂, e₂₂, and g₁₂. Clearly, the all subcells stress allowables are unrealistically high as they require every point in the composite to reach the local allowable stress. Obviously, global failure occurs much sooner in real-world structures after only a few local failures initiate.

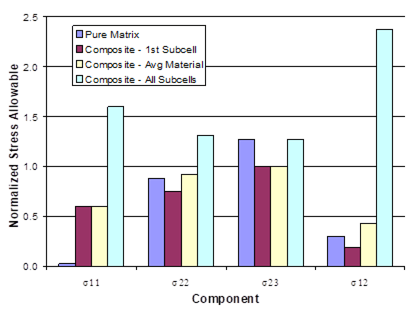
Figure 5.1 Example 5a: Specified matrix and calculated composite stress allowables normalized by the fiber stress allowables for 60% unidirectional graphite/epoxy.

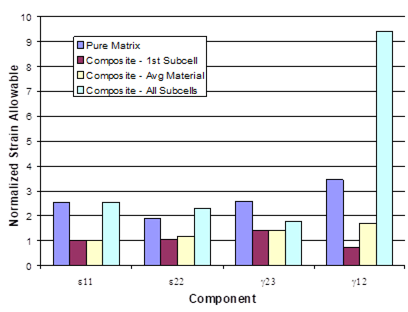
Figure 5.2 Example 5a: Specified matrix and calculated composite strain allowables normalized by the fiber strain allowables for 60% unidirectional graphite/epoxy.

Example 5b: Subcell Static Failure Analysis

In MAC/GMC 4.0, static failure analysis is completely different from the allowables estimation presented in Example 5a. Since the composite allowables are estimated based on a quick elastic concentration analysis, composite static failure analysis is associated with an entire simulated loading history. During each increment of the applied loading, the specified RUC or subcell failure criteria are checked to determine if failure has occurred. Thus, inelasticity, residual stresses, and even damage can be incorporated within a static failure simulation, giving such a simulation the potential to be considerably more accurate than an allowables estimation. Unlike the estimated allowables, however, a failure stress determined via a MAC/GMC 4.0 simulation is not a property-like quantity for a particular composite. The value can change dramatically based on the loading history applied. Note that the identical graphite/epoxy composite employed in Example 5a is employed in the present example. Now, however, simulated thermal and mechanical loading is applied.

MAC/GMC Input File: example_5b.mac

MAC/GMC 4.0 Example 5b - Subcell static failure analysis

*CONSTITUENTS

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=388.2E3,390.E3

ET=7.6E3,7.6E3

NUA=0.41,0.41

NUT=0.45,0.45

GA=14.9E3,15.1E3

ALPA=-0.68E-6,-0.45E-6

ALPT=9.74E-6,10.34E-6

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=3.45E3,3.10E3

ET=3.45E3,3.10E3

NUA=0.35,0.35

NUT=0.35,0.35

GA=1.278E3,1.148E3

ALPA=45.E-6,55.E-6

ALPT=45.E-6,55.E-6

*RUC

MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

*MECH

LOP=2

NPT=2 TI=0.,100. MAG=0.,0.02 MODE=1

# LOP=2 REFTIME=100.

# NPT=3 TI=0.,100.,200. MAG=0.,0.,0.02 MODE=2,1

*THERM

NPT=2 TI=0.,100. TEMP=23.,23.

# NPT=3 TI=0.,100.,200. TEMP=150.,23.,23.

*SOLVER

METHOD=1 NPT=2 TI=0.,100. STP=0.1

# METHOD=1 NPT=3 TI=0.,100.,200. STP=5.,0.1

*ALLOWABLES

NMAT=2

MAT=1

S11=3500. S22=91.2 S33=91.2 S23=31.4 S13=134. S12=134. COMPR=SAM

E11=0.009 E22=0.012 E33=0.012 E23=0.012 E13=0.009 E12=0.009 COMPR=SAM

MAT=2

S11=80. S22=80. S33=80. S23=40. S13=40. S12=40. COMPR=SAM

E11=0.023 E22=0.023 E33=0.023 E23=0.031 E13=0.031 E12=0.031 COMPR=SAM

*FAILURE_SUBCELL

NMAT=2

MAT=1 NCRIT=2

CRIT=1 X11=3500. X22=91.2 X33=91.2 X23=31.4 X13=134. X12=134. &

COMPR=OFF ACTION=1

CRIT=2 X11=0.009 X22=0.012 X33=0.012 X23=0.012 X13=0.009 X12=0.009 &

COMPR=OFF ACTION=1

MAT=2 NCRIT=2

CRIT=1 X11=80. X22=80. X33=80. X23=40. X13=40. X12=40. &

COMPR=OFF ACTION=1

CRIT=2 X11=0.023 X22=0.023 X33=0.023 X23=0.031 X13=0.031 X12=0.031 &

COMPR=OFF ACTION=1

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=1

NAME=example_5b X=2 Y=8

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Constitutive models: Elastic (CMOD=6)

Materials: User-defined (Graphite) (MATID=U)

User-defined (Epoxy) (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 4.1

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 26´26 circular fiber approx., rect. pack (ARCHID=13)

Fiber volume fraction: 0.60 (VF=0.60)

Unit cell aspect ratio: 1.0 (square pack) (R=1.0)

Material assignment: graphite fiber (F=1)

epoxy matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 2 (LOP=2)

Without residual

Number of points: 2 (NPT=2)

Time points: 0., 100. sec. (TI=0.,100.)

Load magnitudes: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

With residual

Reference strain time: 100. sec. (REFTIME=100.)

Number of points: 3 (NPT=3)

Time points: 0., 100., 200. sec. (TI=0.,100.,200.)

Load magnitudes: 0., 0.02 (MAG=0.,0.,0.02)

Loading mode: stress control, strain control (MODE=2,1)

F Note: The appropriate lines must be commented and uncommented to execute with and without residual.

b) Thermal (*THERM) [KM_4]:

Without residual

Number of points: 2 (NPT=2)

Time points: 0., 100. sec. (TI=0.,100.)

Temperature points: 23., 23. (TEMP=23.,23.)

With residual

Number of points: 3 (NPT=3)

Time points: 0., 100., 200. sec. (TI=0.,100.,200.)

Temperature points: 150., 23., 23. (TEMP=150.,23.,23.)

F Note: The appropriate lines must be commented and uncommented to execute with and without residual.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Without residual

Number of points: 2 (NPT=2)

Time points: 0., 100. sec. (TI=0.,100.)

Time step size: 0.1 sec. (STP=0.1)

With residual

Number of points: 3 (NPT=3)

Time points: 0., 100., 200. sec. (TI=0.,100.,200.)

Time step sizes: 5., 0.1 sec. (STP=5.,0.1)

F Note: The small step size is employed during the mechanical loading despite the elastic response of the composite is employed in order to detect failure as soon as it occurs. The appropriate lines must be commented and uncommented to execute with and without residual.

5) Damage and Failure:

a) Stress and strain allowables estimation (*ALLOWABLES) [KM_5]:

Number of materials: 2 (NMAT=2)

Fiber stress allowables: s₁₁ = 3500. MPa (S11=3500.)

(MAT=1) s₂₂ = 91.2 MPa (S22=91.2)

s₃₃ = 91.2 MPa (S33=91.2)

s₂₃ = 31.4 MPa (S23=31.4)

s₁₃ = 134. MPa (S13=134.)

s₁₂ = 134. MPa (S12=134.)

Fiber strain allowables: e₁₁ = 0.009 (E11=0.009)

e₂₂ = 0.012 (E22=0.012)

e₃₃ = 0.012 (E33=0.012)

g₂₃ = 0.012 (E23=0.012)

g₁₃ = 0.009 (E13=0.009)

g₁₂ = 0.009 (E12=0.009)

Fiber compression flag: Compression same as tension (COMPR=SAM)

Matrix stress allowables: s₁₁ = 80. MPa (S11=80.)

(MAT=2) s₂₂ = 80. MPa (S22=80.)

s₃₃ = 80. MPa (S33=80.)

s₂₃ = 40. MPa (S23=40.)

s₁₃ = 40. MPa (S13=40.)

s₁₂ = 40. MPa (S12=40.)

Matrix strain allowables: e₁₁ = 0.023 (E11=0.023)

e₂₂ = 0.023 (E22=0.023)

e₃₃ = 0.023 (E33=0.023)

g₂₃ = 0.031 (E23=0.031)

g₁₃ = 0.031 (E13=0.031)

g₁₂ = 0.031 (E12=0.031)

Matrix compression flag: Compression same as tension (COMPR=SAM)

b) Subcell static failure analysis (*FAILURE_SUBCELL) [KM_5]:

Number of materials: 2 (NMAT=2)

Material #1 (MAT=1)

Number of criteria: 2 (NCRIT=2)

Criterion #1: Maximum stress criterion (CRIT=1)

Failure stresses: s₁₁ = 3500. MPa (X11=3500.)

s₂₂ = 91.2 MPa (X22=91.2)

s₃₃ = 91.2 MPa (X33=91.2)

s₂₃ = 31.4 MPa (X23=31.4)

s₁₃ = 134. MPa (X13=134.)

s₁₂ = 134. MPa (X12=134.)

Criterion #2: Maximum strain criterion (CRIT=2)

Failure strains: e₁₁ = 0.009 (X11=0.009)

e₂₂ = 0.012 (X22=0.012)

e₃₃ = 0.012 (X33=0.012)

g₂₃ = 0.012 (X23=0.012)

g₁₃ = 0.009 (X13=0.009)

g₁₂ = 0.009 (X12=0.009)

Compression flag: Do not check for compressive failure (COMPR=OFF)

Action to take upon failure: Zero subcell stiffness and continue (ACTION=1)

Material #2 (MAT=2)

Number of criteria: 2 (NCRIT=2)

Criterion #1: Maximum stress criterion (CRIT=1)

Failure stresses: s₁₁ = 80. MPa (X11=80.)

s₂₂ = 80. MPa (X22=80.)

s₃₃ = 80. MPa (X33=80.)

s₂₃ = 40. MPa (X23=40.)

s₁₃ = 40. MPa (X13=40.)

s₁₂ = 40. MPa (X12=40.)

Criterion #2: Maximum strain criterion (CRIT=2)

Failure strains: e₁₁ = 0.023 (X11=0.023)

e₂₂ = 0.023 (X22=0.023)

e₃₃ = 0.023 (X33=0.023)

g₂₃ = 0.031 (X23=0.031)

g₁₃ = 0.031 (X13=0.031)

g₁₂ = 0.031 (X12=0.031)

Compression flag: Do not check for compressive failure (COMPR=OFF)

Action to take upon failure: Zero subcell stiffness and continue (ACTION=1)

MAC/GMC 4.0 includes three failure criteria: maximum stress (CRIT=1), maximum strain (CRIT=2), and Tsai-Hill (CRIT=3). For all three criteria, the input takes the same form where the critical failure values for each component are specified as Xij=. As in the allowables calculation, the subcell static failure analysis requires a flag to indicate how to handle compression (COMPR=) (this should be omitted in the case of the Tsai-Hill Criterion). In addition, subcell static failure analysis requires specification of the action to take upon detection of a subcell failure (ACTION=). A value of -1 indicates that the code should stop the execution upon 1^st failure, a value of 0 indicates that the code should only write notification of the failure to the output file and continue, and a value of 1 indicates that the code should treat the subcell as completely damage (i.e., zero the subcell’s stiffness) and continue the execution. For more information on subcell static failure analysis, see the MAC/GMC 4.0 Theory Manual Section 5.2 and the MAC/GMC 4.0 Keywords Manual Section 5.

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT):

Frequency: 1 (FREQ=1)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_5b (NAME=example_5b)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

The results for Example Problem 5b are shown in Figure 5.3 in the form of the transverse stress-strain response of the composite with and without residual stresses included. Without residual stresses, the failure of the first matrix subcell occurs at 68.1 MPa (due to the maximum stress criterion), which corresponds to the 1^st subcell transverse allowable stress estimated for the composite in Example 5a. Because ACTION was set to 1, the subcell(s) that failed at this point have their stiffnesses set to zero, which causes the dramatic drop in the stress-strain response evident in Figure 5.3. Further, the following notification of subcell failure is written to the output file:

******* SUBCELL FAILURE ******

SUBCELL # 13 MATERIAL # 2

FAILED DUE TO THE MAX STRESS CRITERION

COMPONENT = 2

STRESS = 80.0299221493631

ALLOWABLE STRESS = 80.0000000000000

ACTION = 1 ----> ZERO SUBCELL AND CONTINUE

******* SUBCELL FAILURE ******

SUBCELL # 14 MATERIAL # 2

FAILED DUE TO THE MAX STRESS CRITERION

COMPONENT = 2

STRESS = 80.0299221493631

ALLOWABLE STRESS = 80.0000000000000

ACTION = 1 ----> ZERO SUBCELL AND CONTINUE

******* SUBCELL FAILURE ******

SUBCELL # 663 MATERIAL # 2

FAILED DUE TO THE MAX STRESS CRITERION

COMPONENT = 2

STRESS = 80.0299221493631

ALLOWABLE STRESS = 80.0000000000000

ACTION = 1 ----> ZERO SUBCELL AND CONTINUE

******* SUBCELL FAILURE ******

SUBCELL # 664 MATERIAL # 2

FAILED DUE TO THE MAX STRESS CRITERION

COMPONENT = 2

STRESS = 80.0299221493631

ALLOWABLE STRESS = 80.0000000000000

ACTION = 1 ----> ZERO SUBCELL AND CONTINUE

So clearly, four subcells have failed due to the maximum stress criterion. Because the simulated transverse loading is applied under strain control, it can continue despite the drop in the stress-strain response. These drops are due to the instantaneous “zeroing” of the failed subcells stiffness properties. Less dramatic drops would be present were this problem analyzed using HFGMC. As the loading continues in Figure 5.3, additional subcell failures occur, resulting in more drops in the composite transverse response. Clearly, the predicted response without residual stresses reaches its maximum stress just prior to the 1^st subcell failure, and as such, this is the predicted composite transverse UTS.

Also plotted in Figure 5.3 is the predicted transverse response of the graphite/epoxy composite in which residual stresses have been included via a simulated cool down from 150 °C. This is intended to simulate the cure temperature of the composite. Now, even though all subcell failure parameters are identical to the case without residual, 1^st subcell failure is delayed until the composite reaches a global stress of 77.4 MPa. This is because during the simulated cool down, the matrix is placed in a state of residual transverse compression. Then, upon application of the simulated transverse mechanical loading, this transverse residual compression must first be overcome in addition to loading the matrix subcells to their transverse tensile strength of 80 MPa. Note that, even when residual stresses are included, the estimated allowables for the composite are identical to those presented in Example 5a as the allowables are calculated as a first step in the code’s execution and are not linked to the applied loading. In this example, however, it is clear that the MAC/GMC 4.0 subcell static failure analysis is linked to the applied loading. For identical failure parameters, the simulations with and without residual stresses differ by 9.3 MPa (13.7%) in their transverse UTS predictions for the graphite/epoxy composite. It should be noted that, without micromechanics, this effect could not be predicted.

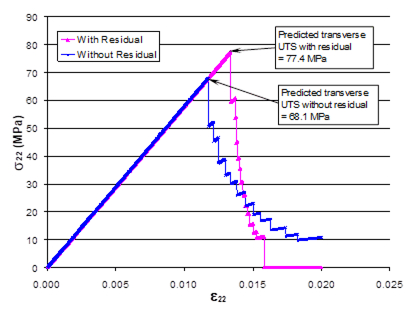
Figure 5.3 Example 5b: Simulated transverse static failure response of unidirection 60% graphite/epoxy at room temperature with and without residual stresses included.

Example 5c: Laminate Static Failure Analysis

In this example problem, a 60% fiber volume fraction graphite/epoxy composite is again considered, as in Examples 5a and 5b. However, now a quasi-isotropic [0°/45°/-45°/90°]_s laminate is the subject of static failure analysis utilizing both the subcell and RUC static failure analysis options. Biaxial loading (N_xx-N_yy) is applied to the laminate, and by altering the load magnitudes applied in the two directions, a plot of the predicted laminate “failure surface” is generated. This “failure surface” is the locus of points in the plane of the applied biaxial stress loading at which failure occurs. Unlike the MAC/GMC 4.0 yield surface capabilities, this failure surface analysis procedure is not automated at this time.

MAC/GMC Input File: example_5c.mac

MAC/GMC 4.0 Example 5c - Laminate static failure analysis

*CONSTITUENTS

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=388.2E3,390.E3

ET=7.6E3,7.6E3

NUA=0.41,0.41

NUT=0.45,0.45

GA=14.9E3,15.1E3

ALPA=-0.68E-6,-0.45E-6

ALPT=9.74E-6,10.34E-6

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=3.45E3,3.10E3

ET=3.45E3,3.10E3

NUA=0.35,0.35

NUT=0.35,0.35

GA=1.278E3,1.148E3

ALPA=45.E-6,55.E-6

ALPT=45.E-6,55.E-6

*LAMINATE

NLY=7

LY=1 THK=0.125 ANG=0 MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

LY=2 THK=0.125 ANG=45 MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

LY=3 THK=0.125 ANG=-45 MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

LY=4 THK=0.250 ANG=90 MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

LY=5 THK=0.125 ANG=-45 MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

LY=6 THK=0.125 ANG=45 MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

LY=7 THK=0.125 ANG=0 MOD=2 ARCHID=13 VF=0.60 R=1. F=1 M=2

*MECH

LOP=99

NPT=2 TI=0.,100. MAG=0.,2000 MODE=2

NPT=2 TI=0.,100. MAG=0.,0. MODE=2

*THERM

NPT=2 TI=0.,100. TEMP=23.,23.

*SOLVER

METHOD=1 NPT=2 TI=0.,100. STP=0.1

*FAILURE_SUBCELL

NMAT=2

MAT=1 NCRIT=1

CRIT=3 X11=3500. X22=91.2 X33=91.2 X23=31.4 X13=134. X12=134. &

ACTION=-1

MAT=2 NCRIT=1

CRIT=3 X11=80. X22=80. X33=80. X23=40. X13=40. X12=40. &

ACTION=-1

#*FAILURE_CELL

# NCRIT=1

# -- Data from 1st subcell allowables (Example 5a)

# CRIT=3 X11=2112. X22=68.08 X33=68.08 X23=31.4 X13=24.89 X12=24.89 &

# ACTION=-1

# -- Data from avg material allowables (Example 5a)

# CRIT=3 X11=2112. X22=84.16 X33=84.16 X23=31.4 X13=57.64 X12=57.64 &

# ACTION=-1

*PRINT

NPL=6

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Constitutive models: Elastic (CMOD=6)

Materials: User-defined (Graphite) (MATID=U)

User-defined (Epoxy) (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 4.1

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 7 (NLY=7)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Volume fraction	Aspect ratio	Fiber material	Matrix material
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(VF)	(R)	(F)	(M)
1	GMC-2D	0.125	0°	26´26 circle rect. pack	0.60	1.	graphite	epoxy
2	GMC-2D	0.125	45°	26´26 circle rect. pack	0.60	1.	graphite	epoxy
3	GMC-2D	0.125	-45°	26´26 circle rect. pack	0.60	1.	graphite	epoxy
4	GMC-2D	0.25	90°	26´26 circle rect. pack	0.60	1.	graphite	epoxy
5	GMC-2D	0.125	-45°	26´26 circle rect. pack	0.60	1.	graphite	epoxy
6	GMC-2D	0.125	45°	26´26 circle rect. pack	0.60	1.	graphite	epoxy
7	GMC-2D	0.125	0°	26´26 circle rect. pack	0.60	1.	graphite	epoxy

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: general loading (LOP=99)

Component #1 ( or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		100.
Magnitudes (MAG=)	0.		2000. MPa ´ thickness
Control (MODE=)		force resultant

Component #2 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		100.
Magnitudes (MAG=)	0.		2000. MPa ´ thickness
Control (MODE=)		stress

Component #3 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		100.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		force resultant

Component #4 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		100.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		moment resultant

Component #5 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		100.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		moment resultant

Component #6 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		100.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		moment resultant

F Note: To generate the “failure surface” shown in the results for this example problem, the magnitudes of the component #1 and #2 applied loads must be adjusted accordingly. For example, applying N_xx=0 and N_yy=2000 MPa ´ thickness will allow the determination of the failure points on the positive N_yy -axis in Figure 5.4.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 100. sec. (TI=0.,100.)

Temperature points: 23., 23. (TEMP=23.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 100. sec. (TI=0.,100.)

Time step size: 0.1 sec. (STP=0.1)

5) Damage and Failure:

a) Subcell static failure analysis (*FAILURE_SUBCELL) [KM_5]:

Number of materials: 2 (NMAT=2)

Material #1 (MAT=1)

Number of criteria: 1 (NCRIT=1)

Criterion #1: Tsai-Hill criterion (CRIT=3)

Failure stresses: s₁₁ = 3500. MPa (X11=3500.)

s₂₂ = 91.2 MPa (X22=91.2)

s₃₃ = 91.2 MPa (X33=91.2)

s₂₃ = 31.4 MPa (X23=31.4)

s₁₃ = 134. MPa (X13=134.)

s₁₂ = 134. MPa (X12=134.)

Action to take upon failure: Stop execution (ACTION=-1)

Material #2 (MAT=2)

Number of criteria: 1 (NCRIT=1)

Criterion #1: Tsai-Hill criterion (CRIT=3)

Failure stresses: s₁₁ = 80. MPa (X11=80.)

s₂₂ = 80. MPa (X22=80.)

s₃₃ = 80. MPa (X33=80.)

s₂₃ = 40. MPa (X23=40.)

s₁₃ = 40. MPa (X13=40.)

s₁₂ = 40. MPa (X12=40.)

Action to take upon failure: Stop execution (ACTION=-1)

b) RUC static failure analysis (*FAILURE_CELL) [KM_5]:

Number of criteria: 1 (NCRIT=1)

Criterion #1: Tsai-Hill criterion (CRIT=3)

Data From 1^st Subcell Allowables for Composite

Failure stresses: s₁₁ = 2112. MPa (X11=2112.)

s₂₂ = 68.08 MPa (X22=68.08)

s₃₃ = 68.08 MPa (X33=68.08)

s₂₃ = 31.4 MPa (X23=31.4)

s₁₃ = 24.89 MPa (X13=24.89)

s₁₂ = 24.89 MPa (X12=24.89)

Data From Avg. Material Allowables for Composite

Failure stresses: s₁₁ = 2112. MPa (X11=2112.)

s₂₂ = 84.16 MPa (X22=84.16)

s₃₃ = 84.16 MPa (X33=84.16)

s₂₃ = 31.4 MPa (X23=31.4)

s₁₃ = 57.64 MPa (X13=57.64)

s₁₂ = 57.64 MPa (X12=57.64)

Action to take upon failure: Stop execution (ACTION=-1)

The RUC level failure analysis input data is similar to the input data for subcell static failure analysis. As with the subcell static failure capabilities, MAC/GMC 4.0 includes the maximum stress and strain criteria, as well as the Tsai-Hill criterion within its RUC static failure capabilities. In this example problem, two sets of RUC static failure parameters are included within the input file (both of which are commented in the input file above). These two sets of data were taken from the allowables estimated for the unidirectional graphite/epoxy composite (which occupies each of the seven plies in the present example) in Example Problem 5a. One set corresponds to the 1^st subcell failure allowable stresses, while the other corresponds to the average material failure allowable stresses.

In order to execute the code to generate all of the results shown below, the appropriate lines in the input file must be commented and uncommented such that only one RUC static failure criterion is active with the subcell failure criteria inactive or such that only the subcell failure criteria are active.

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

For the case that utilizes the subcell static failure criterion and identical s₁₁ and s₂₂ mechanical loading rates (as shown in the input file above), the laminate reaches 1^st subcell failure at an applied force resultant level of N_xx = N_yy = 774 MPa ´ thickness. At this point the code stops execution in accordance with the specified ACTION=-1, and the following is written to the output file:

******* SUBCELL FAILURE ******

LAYER # 1 INTEGRATION POINT #1

SUBCELL # 325 MATERIAL # 1

FAILED DUE TO THE TSAI-HILL CRITERION

STRESSES: 0.2470E+04 0.6041E+02 -0.4911E+01

0.0000E+00 0.0000E+00 0.1427E-07

TSAI-HILL FUNCTION = 1.00000697203627

ALLOWABLE FUNCTION = 1.00000000000000

ACTION = -1 ----> STOP EXECUTION

As stated above, by altering the ratio of the applied N_xx and N_yy loading, the “failure surfaces” shown in Figure 5.4 can be generated. To generate the three distinct failure surfaces, the failure simulation is switched between the two sets of RUC failure parameters (1^st Cell Failure surfaces) and the subcell failure criteria (1^st Subcell Failure surfaces). Figure 5.4 shows that localizing all the way to the level of the subcells within each ply of the laminate in order to generate the 1^st Subcell Failure surface for the laminate gives very similar results to the surface generated by localizing only to the level of the RUC within each ply and using the previously generated 1^st subcell allowables for the RUC failure stresses. Employing the average material allowables for the RUC failure stresses, however, produces a much larger (i.e., less conservative) laminate failure surface.

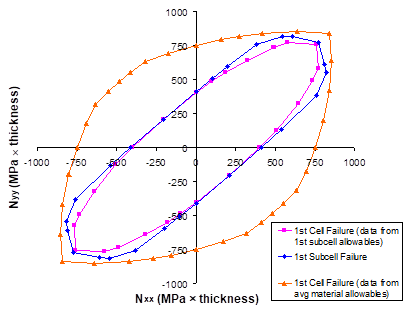
Figure 5.4 Example 5c: Predicted failure surfaces for a 60% fiber volume fraction quasi-isotropic graphite/epoxy laminate at room temperature. Note that these failure surfaces were generated by manually adjusting the ratio of the applied N_xx and N_yy.

Example 5d: Fatigue Damage Analysis

MAC/GMC 4.0 includes two fatigue damage models that function on the local subcell level, both of which are employed in this example problem. The first involves degradation of the subcell material stiffness properties due to applied cyclic loading (suitable for modeling the composite matrix behavior), while the second involves degradation of the subcell material strength properties (suitable for modeling the composite fiber behavior). The same 60% fiber volume fraction graphite/epoxy composite is again considered as both a unidirectional composite and a quasi-isotropic laminate.

The first step in this example problem involves characterizing the epoxy and graphite phases in terms of the fatigue damage model parameters. First, considering the epoxy matrix, the stiffness degradation fatigue damage model will be employed. The transversely isotropic form of this damage model present within MAC/GMC 4.0 is multi-axial, isothermal, and it employs a single scalar internal damage parameter, D (Arnold and Kruch, 1994). This damage parameter begins at zero for an undamaged material and grows (for a particular subcell) as damage occurs due to cyclic loading. The stiffness of the material in a damaged subcell is reduced by a factor of (1 – D) to account for the damage. A value of D = 1 corresponds to the completely damaged (zero stiffness) case. When employed (as in this example) to model the fatigue behavior of the isotropic material present within a particular subcell, this model reduces to the NonLinear Cumulative Damage Rule (NLCDR) developed at ONERA (Wilt et al., 1997). For details on this fatigue damage model, see the MAC/GMC 4.0 Theory Manual Section 5.3.

For an isotropic material, the damage parameters that must be selected reduce to and , and the pertinent equation relating the fatigue life of the isotropic material to the cyclic stress state is,

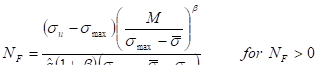
where is the material ultimate strength, is the material fatigue limit (stress below which damage does not occur), is the maximum stress during a loading cycle, is the mean stress during a loading cycle, and is the number of cycles to failure. Note that, in the terminology of Arnold and Kruch (1994), . Utilizing the above equation, the damage model parameters and can be selected for an isotropic material based on the material’s S-N curve (stress level vs. cycles to failure). A suggested characterization procedure for this damage model can be found in Arnold and Kruch (1994).

An S-N curve for epoxy was obtained from Plastics Design Library (1995), and the fatigue damage model parameters were selected as MPa, , and , with MPa, and MPa. A plot showing the fatigue model characterization is given in Figure 5.5.

The second damage model within MAC/GMC 4.0 is much simpler and involves degradation of a material’s strength due to cyclic loading. As shown by Wilt et al. (1997), this type of damage model can be used to simulate the fatigue behavior of fibers that occurs in-situ during fatigue of a composite. The model assumes a logarithmic relation between the material’s strength and the number of cycles within a certain range such that:

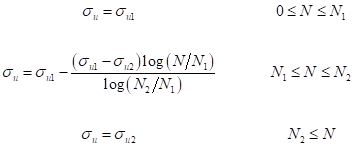
This strength degradation model was employed in the present example to model the longitudinal fatigue behavior of the graphite fiber. The necessary parameters for the model are , and . The values of these parameters chosen for the graphite fiber are shown in Figure 5.6. Note that these data were not correlated with experiment, but rather chosen based on the expected trend.

Given these required parameters for the fatigue damage models for each phase in the graphite/epoxy composite, this example problem, which predicts the fatigue life of a composite and a laminate, can be executed.

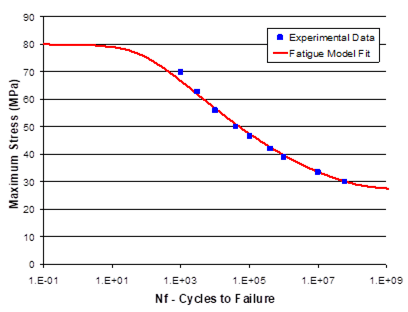
Figure 5.5 Example 5d: Characterization of the stiffness reduction fatigue damage model parameters for the epoxy matrix. Experimental data are from Plastics Design Library (1995).

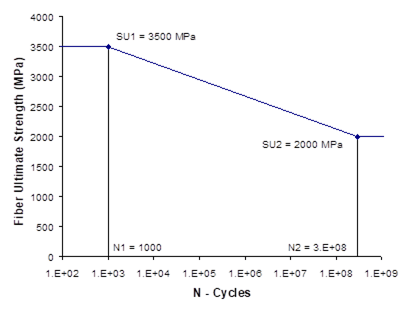
Figure 5.6 Example 5d: Strength reduction fatigue model parameters assumed for the graphite fiber.

MAC/GMC Input File: example_5d.mac

MAC/GMC 4.0 Example 5d - Fatigue damage analysis

*CONSTITUENTS

NMATS=2

# -- Graphite fiber

M=1 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=388.2E3,390.E3

ET=7.6E3,7.6E3

NUA=0.41,0.41

NUT=0.45,0.45

GA=14.9E3,15.1E3

ALPA=-0.68E-6,-0.45E-6

ALPT=9.74E-6,10.34E-6

# -- Epoxy matrix

M=2 CMOD=6 MATID=U MATDB=1

NTP=2

TEM=23.,150.

EA=3.45E3,3.10E3

ET=3.45E3,3.10E3

NUA=0.35,0.35

NUT=0.35,0.35

GA=1.278E3,1.148E3

ALPA=45.E-6,55.E-6

ALPT=45.E-6,55.E-6

*RUC

MOD=2 ARCHID=6 VF=0.60 R=1. F=1 M=2

#*LAMINATE

# NLY=7

# LY=1 THK=0.125 ANG=0 MOD=2 ARCHID=6 R=1. VF=0.60 F=1 M=2

# LY=2 THK=0.125 ANG=45 MOD=2 ARCHID=6 R=1. VF=0.60 F=1 M=2

# LY=3 THK=0.125 ANG=-45 MOD=2 ARCHID=6 R=1. VF=0.60 F=1 M=2

# LY=4 THK=0.250 ANG=90 MOD=2 ARCHID=6 R=1. VF=0.60 F=1 M=2

# LY=5 THK=0.125 ANG=-45 MOD=2 ARCHID=6 R=1. VF=0.60 F=1 M=2

# LY=6 THK=0.125 ANG=45 MOD=2 ARCHID=6 R=1. VF=0.60 F=1 M=2

# LY=7 THK=0.125 ANG=0 MOD=2 ARCHID=6 R=1. VF=0.60 F=1 M=2

*MECH

LOP=2

# LOP=1

NPT=4 TI=0.,50.,150.,200. MAG=0.,40.,-40.,0. MODE=2,2,2

*THERM

NPT=4 TI=0.,50.,150.,200. TEMP=23.,23.,23.,23.

*SOLVER

METHOD=1 NPT=4 TI=0.,50.,150.,200. STP=10.,10.,10.

*DAMAGE

MAXNB=100 DINC=0.2 DMAX=1.0 BLOCK=0.,200.

NDMAT=2

MAT=1 MOD=2 SU1=3500,91.2,91.2,31.4,134.,134 &

SU2=2000.,91.2,91.2,31.4,134.,134. &

N1=1000,1000,1000,1000,1000,1000 &

N2=300000000,300000000,300000000,300000000,300000000,300000000

MAT=2 MOD=1 ANG=0. BN=0.0 BP=0.0 OMU=1. OMFL=1. OMM=1. ETU=1. &

ETFL=1. ETM=1. BE=9. A=0.05 SFL=27. XML=150. &

SU=80.

*FAILURE_SUBCELL

NMAT=2

MAT=1 NCRIT=1

CRIT=1 X11=3500. X22=91.2 X33=91.2 X23=31.4 X13=134. X12=134. &

COMPR=SAM

MAT=2 NCRIT=1

CRIT=1 X11=80. X22=80. X33=80. X23=40. X13=40. X12=40. &

COMPR=SAM

*FAILURE_CELL

NCRIT=1

CRIT=2 X11=0.05 X22=0.05 X33=0.05 X23=0.05 X13=0.05 X12=0.05 &

COMPR=SAM

*PRINT

NPL=3

*XYPLOT

FREQ=1

# LAMINATE=1

# NAME=example_5d X=1 Y=10

MACRO=2

NAME=example_5d_11 LYR=1 X=1 Y=7

NAME=example_5d_22 LYR=1 X=2 Y=8

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Constitutive models: Elastic (CMOD=6)

Materials: User-defined (Graphite) (MATID=U)

User-defined (Epoxy) (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 4.1

3) Analysis type:

a) Unidirectional Composite Case (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 7´7 circular fiber approx., rect. pack (ARCHID=6)

Fiber volume fraction: 0.60 (VF=0.60)

Unit cell aspect ratio: 1.0 (square pack) (R=1.0)

Material assignment: graphite fiber (F=1)

epoxy matrix (M=2)

b) Quasi-Isotropic Laminate Case (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 7 (NLY=7)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Volume fraction	Aspect ratio	Fiber material	Matrix material
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(VF)	(R)	(F)	(M)
1	GMC-2D	0.125	0°	7´7 circle rect. pack	0.60	1.	graphite	epoxy
2	GMC-2D	0.125	45°	7´7 circle rect. pack	0.60	1.	graphite	epoxy
3	GMC-2D	0.125	-45°	7´7 circle rect. pack	0.60	1.	graphite	epoxy
4	GMC-2D	0.25	90°	7´7 circle rect. pack	0.60	1.	graphite	epoxy
5	GMC-2D	0.125	-45°	7´7 circle rect. pack	0.60	1.	graphite	epoxy
6	GMC-2D	0.125	45°	7´7 circle rect. pack	0.60	1.	graphite	epoxy
7	GMC-2D	0.125	0°	7´7 circle rect. pack	0.60	1.	graphite	epoxy

F Note: To generate the data in the Results for both the unidirectional composite and the quasi-isotropic laminate, the appropriate lines in the input file must be commented and uncommented.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 2 or 1 (LOP=2) or (LOP=1)

Number of points: 4 (NPT=4)

Time points: 0., 50., 150., 200. sec. (TI=0.,50.,150.,200.)

Load magnitudes: 0., 40., -40., 0. MPa (MAG=0.,40.,-40.,0.)

Loading mode: stress control (MODE=2,2,2)

For fatigue loading, the loading cycle must be defined in *MECH. This cycle must start and end at the same magnitudes. Since this example involves a fully reversed fatigue simulation, the cycle starts at a stress of 0, rises to 40 MPa, then decreases to -40 MPa, and finally returns to 0.

F Note: To execute the code with different maximum (and minimum) stress levels (i.e., to generate an S-N curve), the magnitudes of the applied loading must be altered and the code executed repeatedly.

F Note: In the case of the laminate, the loading is actual force resultant control. Since the laminate thickness is 1., equivalency exists between the stress magnitudes for the unidirectional composites and the force resultant magnitudes for the laminate.

b) Thermal (*THERM) [KM_4]:

Number of points: 4 (NPT=4)

Time points: 0., 50., 150., 200. sec. (TI=0.,50.,150.,200.)

Temperature points: 23., 23., 23., 23. (TEMP=23.,23.,23.,23.)

As with the mechanical loading, the thermal loading in fatigue damage analysis defines the cycle and must start and end at the same temperature. In this case, the loading cycle does not involve a temperature change.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 4 (NPT=4)

Time points: 0., 50., 150., 200. sec. (TI=0.,50.,150.,200.)

Time step sizes: 10., 10., 10. sec. (STP=10.,10.,10.)

5) Damage and Failure:

a) Fatigue Damage Analysis (*DAMAGE) [KM_5]:

MAXNB=100 DINC=0.2 DMAX=1.0 BLOCK=0.,200.

Max. no. of load blocks: 100 (MAXNB=100)

Damage increment: 0.2 (DINC=0.2)

Max. damage value: 1.0 (DMAX=1.0)

Load block times: 0., 200. sec. (BLOCK=0.,200.)

The load block associated with one cycle is specified using BLOCK= to indicate the start and end times of the load block. This allows additional loading to occur before or after the actual cyclic load block if desired (e.g., to incorporate residual stresses). The MAC/GMC 4.0 fatigue analysis applies this load block and then determines the number of cycles of this load block required to cause the local damage increment specified as DINC=. This is a local increment of the damage parameter, D, which pertains to a single subcell. Since there can be many subcells, each with its own value of D, the code selects a controlling subcell that reaches the damage increment first. The number of cycles (of the specified load block) required to cause the local damage increment is then imposed upon the composite, resulting in a state of damage throughout the composite. Then, the simulated load block is applied again, and a new number of cycles required to increment the local damage (by DINC) is calculated. This process is repeated until the maximum number of load blocks (MAXNB) has been applied or complete failure has occurred. By applying load blocks to increment the damage in this fashion, the stress state in the composite is permitted to redistribute based on the evolving state of damage. In general, a smaller damage increment will cause longer execution times, but also allows a greater degree of load redistribution.

NDMAT=2

MAT=1 MOD=2 SU1=3500,91.2,91.2,31.4,134.,134 &

SU2=2000.,91.2,91.2,31.4,134.,134. &

N1=1000,1000,1000,1000,1000,1000 &

N2=300000000,300000000,300000000,300000000,300000000,300000000

No. damaging materials: 2 (NDMAT=2)

For Material #1 (MAT=1)

Fatigue model: Strength reduction model (MOD=2)

Ultimate stress point 1: s₁₁ = 3500. MPa (SU1=3500.,91.2,…)

s₂₂ = 91.2 MPa

s₃₃ = 91.2 MPa

s₂₃ = 31.4 MPa

s₁₃ = 134. MPa

s₁₂ = 134. MPa

Ultimate stress point 2: s₁₁ =2000. MPa (SU1=2000.,91.2,…)

s₂₂ = 91.2 MPa

s₃₃ = 91.2 MPa

s₂₃ = 31.4 MPa

s₁₃ = 134. MPa

s₁₂ = 134. MPa

Number of cycles point 1: 1000 (N1=1000,1000,…)

Number of cycles point 2: 300,000,000 (N2=300000000,300000000,…)

The ultimate stress points and number of cycles points are listed for the six stress components. In the present example, only the s₁₁ ultimate stress component is changing with number of cycles.

MAT=2 MOD=1 ANG=0. BN=0.0 BP=0.0 OMU=1. OMFL=1. OMM=1. ETU=1. &

ETFL=1. ETM=1. BE=9. A=0.05 SFL=27. XML=150. &

SU=80.

For Material #2 (MAT=2)

Fatigue model: Stiffness reduction model (MOD=1)

q: 0. (ANG=0.)

b: 0.0 (BN=0.0)

b’: 0.0 (BP=0.0)

w_u: 1. (OMU=1.)

w_fl: 1. (OMFL=1.)

w_m: 1. (OMM=1.)

h_u: 1. (ETU=1.)

h_fl: 1. (ETFL=1.)

h_m: 1. (ETM=1.)

b: 9. (BE=9.)

: 0.05 (A=9.)

s_fl: 27. MPa (SFL=27.)

M: 150. MPa (XML=150.)

s_u: 80. MPa (SU=80.)

For the meaning of all stiffness reduction fatigue damage model parameters, see the MAC/GMC 4.0 Theory Manual Section 5.3. For an isotropic material such as epoxy, the last 5 parameters listed are all that must be selected.

b) Subcell static failure analysis (*FAILURE_SUBCELL) [KM_5]:

Number of materials: 2 (NMAT=1)

Material #1 (MAT=1)

Number of criteria: 1 (NCRIT=1)

Criterion #1: Maximum stress criterion (CRIT=1)

Failure stresses: s₁₁ = 3500. MPa (X11=3500.)

s₂₂ = 91.2 MPa (X22=91.2)

s₃₃ = 91.2 MPa (X33=91.2)

s₂₃ = 31.4 MPa (X23=31.4)

s₁₃ = 134. MPa (X13=134.)

s₁₂ = 134. MPa (X12=134.)

Compression flag: Compressive strengths same as tensile (COMPR=SAM)

Material #2 (MAT=2)

Number of criteria: 1 (NCRIT=1)

Criterion #1: Maximum stress criterion (CRIT=1)

Failure stresses: s₁₁ = 80. MPa (X11=80.)

s₂₂ = 80. MPa (X22=80.)

s₃₃ = 80. MPa (X33=80.)

s₂₃ = 40. MPa (X23=40.)

s₁₃ = 40. MPa (X13=40.)

s₁₂ = 40. MPa (X12=40.)

Compression flag: Compressive strengths same as tensile (COMPR=SAM)

F Note: In the case of fatigue damage analysis, ACTION is not needed because the fatigue analysis must continue until overall failure or the maximum number of load blocks is applied. If ACTION is specified in this case, it will be ignored by the code.

c) RUC static failure analysis (*FAILURE_CELL) [KM_5]:

Number of criteria: 1 (NCRIT=1)

Criterion #1: Maximum strain criterion (CRIT=2)

Failure strains: e₁₁ = 0.05 (X11=0.05)

e₂₂ = 0.05 (X22=0.05)

e₃₃ = 0.05 (X33=0.05)

e₂₃ = 0.05 (X23=0.05)

e₁₃ = 0.05 (X13=0.05)

e₁₂ = 0.05 (X12=0.05)

Compression flag: Compressive strains same as tensile (COMPR=SAM)

In the present example, the RUC static failure analysis option is employed to limit the amount of strain permitted for an RUC. This allows the code to treat the RUC as failed if damage has occurred such that the stiffness of the RUC is very low and a large strain results. Limiting the strain in this matter can also prevent numerical overflow when the loading is in stress control, as in the present example. The RUC level static failure capabilities function similarly to the subcell level static failure capabilities. The code simply employs the global quantities rather than the local quantities when evaluating the appropriate failure criteria.

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 3 (NPL=3)

b) x-y plots (*XYPLOT):

Frequency: 1 (FREQ=1)

Number of laminate plots: 1 (LAMINATE=1)

Laminate plot names: example_5d (NAME=example_5d)

Laminate x-y quantities: (X=1 Y=10)

Number of macro plots: 2 (MACRO=2)

Macro plot names: example_5d_11 (NAME=example_5d_11)

example_5d_22 (NAME=example_5d_22)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

ε₂₂, σ₂₂ (X=2 Y=8)

Number of micro plots: 0 (MICRO=0)

F Note: In this example, the lines from the input file associated with the laminate plots should be commented for the RUC analyses.

7) End of file keyword: (*END)

Results

Results for the fatigue damage analysis are written not only to the MAC/GMC 4.0 output file, but also to a damage file. This damage file is given the same name as the output file, with _dam.data appended. Thus, in the present example, the damage file is named “example_5d_dam.data”. This file includes a summary of the damage calculations and state of damage after each applied load block, as well as the total number of cycles to failure. A portion of this file is shown below:

Completed Applied Load Block Number 3 (Loading Increment Number 60 )

----------------------------------------------------------------------------

A) Cycles Required to Incur a Damage Increment of DINC = 0.2000

Controlling subcell ---> 46

Number of Cycles => 1460.389

Number of Cycles => 1460.000 (rounded)

---------------------------------------------------

B) Current TOTAL number of cycles ---> 7530637

(after applied load cycle 3, D = 0.5999 )

---------------------------------------------------

C) Current Damage in each subcell (after 7530637 cycles):

Subcell NF* D

------- ------- -------

1 - inf - 0.0000

2 - inf - 0.0000

3 0.2876E+09 0.0000

4 1486.0947 0.5993

5 0.2876E+09 0.0000

6 - inf - 0.0000

7 - inf - 0.0000

8 - inf - 0.0000

. ® Lines Omitted

*NOTE: NF = Remaining life assuming no further stress redistribution

. ® Lines Omitted

********************************************

* ALL SUBCELLS HAVE FAILED *

* TOTAL NUMBER OF CYCLES = 7530637.0 *

* *

********************************************

Results from the x-y plot file are shown in Figure 5.7 for a transverse fatigue analysis of the unidirectional 60% graphite/epoxy composite. In this case, it was determined that 7,517,751 cycles of load block #1 were required to achieve a damage level of 0.2 in a subcell. Then, load block #2 was applied, and, as shown in Figure 5.7, the transverse composite response becomes more compliant due to the damage state caused by the 7,517,751 cycles of load block #1. Only 11,426 cycles of load block #2 are required to cause a local damage increment of 0.2, resulting in a total number of cycles of 7,529,177. When load block #3 is applied, the transverse composite response is even more compliant due to the higher level of damage throughout the composite. Only 1,460 cycles of load block #3 are required to cause an additional local damage increment of 0.2. During applied load block #4 local failures occur that cause the non-linearity evident in Figure 5.7. Then, when the code attempts to apply load block #5, additional failures occur that lead to the complete failure of the composite. That is, after application of load block #4, the code cannot withstand any additional cycles. The predicted life of the composite is 7,530,637 cycles.

By altering the applied stress magnitudes in *MECH, a transverse S-N curve can be predicted for the graphite/epoxy composite. Similarly, by altering the loading option, a longitudinal S-N curve for the composite can be predicted. Finally, switching the simulation to a laminate fatigue analysis (commenting *RUC and uncommenting *LAMINATE in the input file), an S-N curve for the quasi-isotropic laminate can be predicted. All three of these predicted S-N curves are plotted in Figure 5.8, whereas, for additional detail, each S-N curve is plotted separately in Figure 5.9, Figure 5.10, and Figure 5.11. As one would expect, the S-N curve for the longitudinal composite is highest due to the strong and stiff fibers oriented along the loading direction. The transverse S-N curve is lowest since the composite’s transverse response is matrix dominated, and the laminate S-N curve is intermediate.

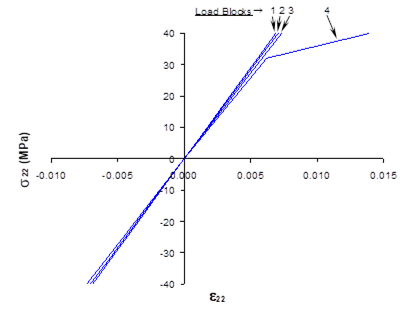
Figure 5.7 Example 5d: Transverse stress-strain response for a 60% graphite/epoxy composite at room temperature for the four applied load blocks prior to failure.

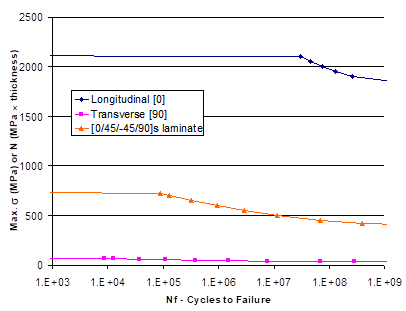
Figure 5.8: Example 5d: Predicted S-N curves for 60% graphite/epoxy at room temperature.

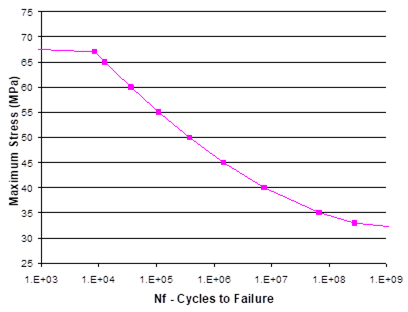
Figure 5.9: Example 5d: Predicted transverse S-N curve for 60% graphite/epoxy at room temperature.

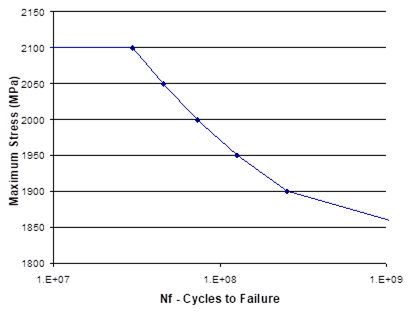
Figure 5.10 Example 5d: Predicted longitudinal S-N curve for 60% graphite/epoxy at room temperature.

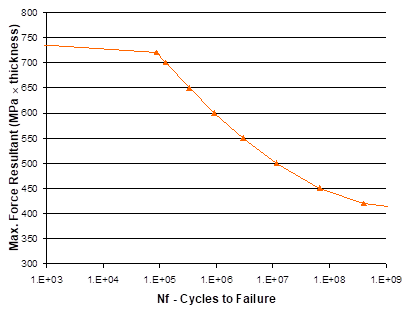
Figure 5.11 Example 5d: Predicted S-N curve for a quasi-isotropic [0°/45°/-45°/90°]_s 60% graphite/epoxy laminate.

Example 5e: Fiber-Matrix Debonding

This example problem involves the simulation of transverse fiber-matrix debonding in a SiC/Ti-21S composite. This type of failure has proven to be a major obstacle in the utilization of titanium matrix composites. MAC/GMC 4.0 incorporates two distinct fiber-matrix debonding models, each of which is based on the same overall concept of imposing a discontinuity or “jump” in displacement at a particular interface. This displacement jump is modeled as proportional to the stress at the interface and is not activated until the interfacial stress reaches a critical debond stress,

where [u] is the resulting displacement component at interface I, s is a particular stress component at interface I, s_DB is the debond stress of interface I, and R is a debonding parameter for interface I. This interfacial representation has been employed by Jones and Whittier (1967), Aboudi (1987), Achenbach and Zhu (1989), and Wilt and Arnold (1996). In MAC/GMC 4.0, as was done by Bednarcyk and Arnold (2002), the debonding parameter R is permitted to evolve with time. The form of this time evolution distinguishes between the two debonding models within MAC/GMC 4.0.

First, the constant compliant interface (CCI) model employs,

at a particular interface. The evolving compliant interface (ECI) model, on the other hand, employs,

at a particular interface. L and B are additional parameters that characterize the behavior of a particular interface and t_DB is the time of debonding for the interface. Thus, the time dependence in the CCI model is implicitly based on the time dependence of the interfacial stress while the ECI model incorporates explicit time dependence in its evolution equation. The dependence of the CCI model on the interfacial stress causes this model to saturate to a steady state condition (when the parameters L and B are chosen properly). This characteristic is due to the fact that, as the parameter R rises with the rising interfacial stress, the interface becomes more and more compliant, causing the interfacial stress to level off. Once the interfacial stress stops increasing, the debonding parameter R can no longer increase, and a steady state condition is reached. Conversely, in the ECI model, with its explicit exponential time dependence, the debonding parameter R can continue to rise. As shown in this example problem, this ability allows the interfacial stress to unload in composite simulations involving the ECI model. For additional information on the CCI and ECI models, see the MAC/GMC 4.0 Theory Manual Section 5.4.

MAC/GMC Input File: example_5e.mac

MAC/GMC 4.0 Example 5e - Fiber-matrix transverse debonding

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=11 VF=0.35 R=0.9 F=1 M=2

*MECH

LOP=3 REFTIME=64800.

NPT=5 TI=0.,24000.,57600.,64800.,64908. MAG=0.,0.,0.,0.,0.018 MODE=2,2,2,1

*THERM

NPT=5 TI=0.,24000.,57600.,64800.,64908. TEMP=900.,534.583,23.,650.,650. %

*SOLVER

METHOD=1 NPT=5 TI=0.,24000.,57600.,64800.,64908. STP=250.,40.,40.,0.2 %

*DEBOND

NII=1

# DBCH=1 NBI=1 NGI=1 FACE=2 BDN=7. LN=0.0001 BN=60. TOLN=0. &

# BDS=40 LS=0.1 BS=100. DELAY=64800.

DBCH=2 NBI=1 NGI=1 FACE=2 BDN=7. LN=0.0001 BN=8. TOLN=0. &

BDS=40 LS=0.1 BS=100 DELAY=64800.

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=1

NAME=example_5e X=3 Y=9

MICRO=1

NAME=example_5e IB=1 IG=2 X=3 Y=9

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: Square fiber, rectangular pack (ARCHID=11)

Unit cell aspect ratio: 0.9 (R=0.9)

Fiber volume fraction: 0.35 (VF=0.35)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 3 (LOP=3)

Strain reference time: 57600. sec. (REFTIME=57600.)

Number of points: 5 (NPT=5)

Time points: 0., 24000., 57600., 64800., 64908. sec. (TI=0.,24000.,…)

Load magnitude: 0., 0., 0., 0., 0.018 (MAG=0.,0.,…,0.018)

Loading mode: stress/strain control (MODE=2,2,2,1)

b) Thermal (*THERM) [KM_4]:

Number of points: 5 (NPT=5)

Time points: 0., 24000., 57600., 64800., 64908. sec. (TI=0.,24000.,…)

Temperature points: 900., 534.583, 23., 650., 650. °C (TEMP=900.,…,650.)

F Note: The second temperature (534.583 °C) is chosen in order to preserve the rate of change of the temperature.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 5 (NPT=5)

Time points: 0., 24000., 57600., 64800., 64908. sec. (TI=0.,24000.,…)

Time step sizes: 250., 40., 40., 0.2 sec. (STP=250.,40.,40.,0.2)

5) Damage and Failure:

a) Fiber-matrix debonding (*DEBOND) [KM_5]:

NII=1

# DBCH=1 NBI=1 NGI=1 FACE=2 BDN=7. LN=0.0001 BN=60. TOLN=0. &

# BDS=40 LS=0.1 BS=100. DELAY=64800.

DBCH=2 NBI=1 NGI=1 FACE=2 BDN=7. LN=0.0001 BN=8. TOLN=0. &

BDS=40 LS=0.1 BS=100 DELAY=64800.

No. debonding interfaces: 1 (NII=1)

CCI Model (DBCH=1)

Interface subcell indices: 1, 1 (NBI=1 NGI=1)

Interface identifier: x₃-interface (FACE=2)

Normal debond stress: 7. ksi (BDN=7.)

Normal L parameter: 0.0001 /ksi (LN=0.0001)

Normal B parameter: 60. s (BN=60.)

Load reversal tolerance: 0. ksi (TOLN=0.)

Shear debond stress: 40. ksi (BDS=40.)

Shear L parameter: 0.1 /ksi (LS=0.1)

Shear B parameter: 100. s (BS=100.)

Debond time delay 64800. sec. (DELAY=64800.)

ECI Model (DBCH=2)

Interface subcell indices: 1, 1 (NBI=1 NGI=1)

Interface identifier: x₃-interface (FACE=2)

Normal debond stress: 7. ksi (BDN=7.)

Normal L parameter: 0.0001 /ksi (LN=0.0001)

Normal B parameter: 60. s (BN=60.)

Load reversal tolerance: 0. ksi (TOLN=0.)

Shear debond stress: 40. ksi (BDS=40.)

Shear L parameter: 0.1 /ksi (LS=0.1)

Shear B parameter: 100. s (BS=100.)

Debond time delay 64800. sec. (DELAY=64800.)

The input format for debonding shown above involves first specifying the number of interfaces that could possibly debond, then specifying the required data for each of these interfaces. MAC/GMC 4.0 treats the normal and shear debonding at a particular interface independently. Thus, independent normal and shear values for the debond stress (s_DB), L parameter, and B parameter are required for each interface that is permitted to debond. In addition, a normal load reversal tolerance (TOLN) and a debond time delay (DELAY) must be specified for each interface. The normal load reversal tolerance is the stress below which the model treats the normal interfacial stress as zero, thus allowing the interface to close and support compressive stress. This can become important in cyclic load cases. The debond time delay is the time at which the code begins to consider the possibility of debonding. Before this time, the interface is treated as perfectly bonded independently of the other specified parameters. For more information on the debonding models and the associated input requirements, see the MAC/GMC 4.0 Theory Manual Section 5.4 and the MAC/GMC 4.0 Keywords Manual Section 5.

F Note: In order to execute the three cases presented in the results for this example, the appropriate lines under *DEBOND must be commented and uncommented.

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_5e (NAME=example_5e)

Macro plot x-y quantities: ε₃₃, σ₃₃ (X=3 Y=9)

Number of micro plots: 1 (MICRO=1)

Micro plot names: example_5e (NAME=example_5e)

Micro plot subcell indices: 1, 2 (IB=1 IG=2)

Micro plot x-y quantities: ε₃₃, σ₃₃ (X=3 Y=9)

7) End of file keyword: (*END)

Results

Figure 5.12 shows the predicted transverse tensile response of the composite at 650 °C for the three different cases (perfect bonding, debonding represented by the CCI model, and debonding represented by the ECI model). Both the global (composite) stress vs. strain response and the local interface stress vs. global strain response are plotted for each case. In the case of perfect bonding, the interfacial stress is higher than the composite stress at a given global strain level. Including fiber-matrix debonding in the simulation via the CCI model has a major effect on the transverse response. The obvious “knee” in the composite curve corresponds to the onset of fiber-matrix debonding. The interface response predicted by the CCI model is identical to the perfectly bonded interface behavior until debonding occurs. Then the interfacial stress quickly saturates to a nearly constant value. Since the interface can support no additional stress, the intact region of the composite is placed under greater stress and flows to a greater extent. Finally, in the case of the ECI model, after the interface debonds, the interfacial stress unloads. This is thought to be the more accurate mechanism as a debonded interface cannot support stress. Now the intact region of the composite must not only support the additional applied load, but also the stress that is unloaded from the interface. This causes even more flow in the intact region, and a composite stress strain curve that is considerably more compliant than that predicted using the CCI model. Note that residual stresses were incorporated in the present example, which is why the interfacial stresses plotted in Figure 5.12 are compressive at zero applied global strain.

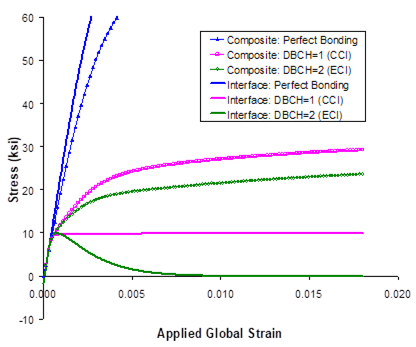
Figure 5.12 Example 5e: Predicted local and global transverse stress-strain response of 35% SiC/Ti-21S at 650 °C with fiber-matrix debonding.

Example 5f: Fiber Breakage

This example problem demonstrates the two methods incorporated within MAC/GMC 4.0 that can be used to model longitudinal fiber breakage in composite materials. The first is the evolving compliant interface (ECI) model, which was applied to transverse fiber-matrix debonding in the previous example problem. Now, instead of applying the ECI model to a fiber-matrix interface, it is applied to an internal fiber interface within a triply periodic RUC. The second model is the Curtin effective fiber breakage model (Curtin, 1991, 1993). This model combines a shear-lag analysis with fiber strength statistics to degrade the stiffness of an effective fiber that represents all fibers within a composite. Both models, as implemented within MAC/GMC 4.0, are capable of predicting the longitudinal strength of continuous fiber composites.

MAC/GMC Input File: example_5f.mac

MAC/GMC 4.0 Example 5f - Fiber breakage

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=1 VF=0.35 F=1 M=2

# MOD=3 ARCHID=99

# NA=1 NB=2 NG=2

# D=1.

# H=0.5916,0.4084

# L=0.5916,0.4084

# SM=1,2

# SM=2,2

*MECH

LOP=1 REFTIME=64800.

NPT=5 TI=0.,24000.,57600.,64800.,64908. MAG=0.,0.,0.,0.,0.018 MODE=2,2,2,1

*THERM

NPT=5 TI=0.,24000.,57600.,64800.,64908. TEMP=900.,534.583,23.,650.,650. %

*SOLVER

METHOD=1 NPT=5 TI=0.,24000.,57600.,64800.,64908. STP=250.,40.,40.,0.2 %

#*DEBOND

# NII=1

# DBCH=2 NAI=1 NBI=1 NGI=1 FACE=1 BDN=311. LN=0.00000001 BN=3. TOLN=0. &

# BDS=400 LS=0.1 BS=100 DELAY=64800.

*CURTIN

NCURT=1

NBI=1 NGI=1 D=142.E-6 L0=0.0127 SIG0=508. TAU0=2.03 M=17.0 &

DELAY=64800. ACTION=0

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=1

NAME=example_5f X=1 Y=7

MICRO=1

NAME=example_5f IA=1 IB=1 IG=1 X=1 Y=7

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Perfect Fiber and Curtin Model Simulations

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: square fiber, square pack (ARCHID=1)

Fiber volume fraction: 0.35 (VF=0.35)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

ECI Model Simulation

Analysis model: Triply periodic GMC (MOD=3)

Architecture: User-defined (ARCHID=99)

No. subcells in x1-dir.: 1 (NA=1)

No. subcells in x2-dir.: 2 (NB=2)

No. subcells in x3-dir.: 2 (NG=2)

Subcell depths: 1. (D=1.0)

Subcell heights: 0.5961,0.4084 (H=0.5961,0.4084)

Subcell lengths: 0.5961,0.4084 (L=0.5961,0.4084)

Material assignment: square fiber, square pack (SM=1,2 / SM=2,2)

F Note: To generate the results for all three cases presented in the results, the appropriate lines in the input file must be commented and uncommented.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 3 (LOP=3)

Strain reference time: 57600. sec. (REFTIME=57600.)

Number of points: 5 (NPT=5)

Time points: 0., 24000., 57600., 64800., 64908. sec. (TI=0.,24000.,…)

Load magnitude: 0., 0., 0., 0., 0.018 (MAG=0.,0.,…,0.018)

Loading mode: stress/strain control (MODE=2,2,2,1)

b) Thermal (*THERM) [KM_4]:

Number of points: 5 (NPT=5)

Time points: 0., 24000., 57600., 64800., 64908. sec. (TI=0.,24000.,…)

Temperature points: 900., 534.583, 23., 650., 650. °C (TEMP=900.,…,650.)

F Note: The second temperature (534.583 °C) is chosen in order to preserve the rate of change of the temperature.

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 5 (NPT=5)

Time points: 0., 24000., 57600., 64800., 64908. sec. (TI=0.,24000.,…)

Time step sizes: 250., 40., 40., 0.2 sec. (STP=250.,40.,40.,0.2)

5) Damage and Failure:

a) Fiber-matrix debonding (*DEBOND) [KM_5]:

No. debonding interfaces: 1 (NII=1)

Interface subcell indices: 1, 1, 1 (NAI=1 NBI=1 NGI=1)

Interface identifier: x₁-interface (FACE=1)

Normal debond stress: 311. ksi (BDN=311.)

Normal L parameter: 0.00000001 /ksi (LN=0.00000001)

Normal B parameter: 3. s (BN=3.)

Load reversal tolerance: 0. ksi (TOLN=0.)

Shear debond stress: 400. ksi (BDS=400.)

Shear L parameter: 0.1 /ksi (LS=0.1)

Shear B parameter: 100. s (BS=100.)

Debond time delay 64800. sec. (DELAY=64800.)

b) Curtin effective fiber breakage model (*CURTIN) [KM_5]:

*CURTIN

NCURT=1

NBI=1 NGI=1 D=142.E-6 L0=0.0127 SIG0=508. TAU0=2.03 M=17.0 &

DELAY=64800. ACTION=0

No. Curtin model fibers: 1 (NCURT=1)

Fiber subcell indices: 1, 1 (NBI=1 NGI=1)

Fiber diameter: 142. mm (D=142.E-6)

Fiber gauge length: 12.7 mm (L0=0.0127)

Fiber mean strength: 508. ksi (SIG0=508.)

Fiber-matrix shear friction: 2.03 ksi (TAU0=2.03)

Fiber Weibull modulus: 17.0 (M=17.0)

Curtin time delay 64800. sec. (DELAY=64800.)

Action to take upon failure: Only write notification and continue (ACTION=0)

The format for specifying the Curtin model data is similar to that employed in the debond model data specification. Most of the Curtin model parameters are physical or statistical in nature and relatively easily obtained. The exception is the fiber-matrix frictional sliding shear stress (TAU0). Attempts have been made to extract this value from fiber push out or pull out tests on the composite, but this can be problematic since the value will then depend on the residual stress state in the particular composite. Hence, the fiber-matrix frictional sliding shear stress may alternately be thought of as an internal parameter. As in the fiber-matrix debonding data, a time delay must be specified in the Curtin model data. Finally, as in the subcell failure data, an action to take upon Curtin model failure of the fiber must be specified.

F Note: In order to execute the three cases presented in the results for this example, the appropriate lines under *DEBOND must be commented and uncommented.

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_5f (NAME=example_5f)

Macro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

Number of micro plots: 1 (MICRO=1)

Micro plot names: example_5e (NAME=example_5e)

Micro plot subcell indices: 1, 1 (IA=1 IB=1 IG=1)

Micro plot x-y quantities: ε₁₁, σ₁₁ (X=1 Y=7)

7) End of file keyword: (*END)

Results

Figure 5.13 shows the predicted longitudinal tensile response of the composite at 650 °C for the three different cases (perfect fiber, ECI model for the fiber, and Curtin model for the fiber). Both the global (composite) stress vs. strain response and the local fiber stress vs. global strain response are plotted for each case. In the present case, the ECI and Curtin models give similar results both locally and globally. Both models cause the fiber response to diverge from that of the perfect fiber case, reach a maximum, and then decrease. Because the present case involves the longitudinal behavior of the continuous fiber composite, the fiber response has a dominant influence on the global composite response. Both the ECI model and Curtin model composite curves reach a maximum at 173 ksi, which may be considered the predicted UTS of the composite. In fact, the following is written to the output file:

CURTIN FAILURE:

> STRESS = 418.189691475676 X = 0.125681408909315

at the time corresponding to the maximum in the Curtin model composite prediction. Were the ACTION specifier under *CURTIN set to -1, execution of the code would have stopped at this point. When employing the ECI model to simulate fiber breakage, it is not possible to stop execution when this maximum in the stress-strain response is reached. After the maximum composite stress is reached, the ECI and Curtin model predictions diverge in what is a non-physical domain of the predictions.

While the ECI and Curtin models give similar results for the present case, the Curtin model is often preferable for modeling the longitudinal fiber breakage behavior of composites. This is because most of the Curtin model parameters have physical interpretation, whereas the ECI model parameters L and B are internal variables with no real physical meaning. As shown by Bednarcyk and Arnold (2001), the ECI model debond stress can be assigned based on fiber strength statistics in an RUC containing multiple fibers, but the internal parameters L and B still remain to be chosen. The advantage of the ECI model is, that by controlling the parameters for each fiber individual, the model can provide some additional flexibility.

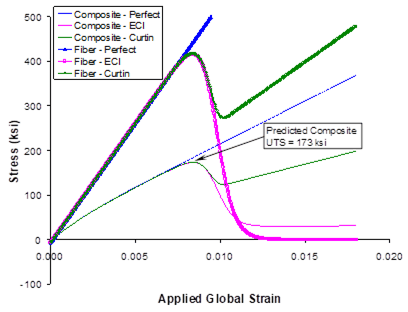
Figure 5.13 Example 5f: Predicted local and global longitudinal stress-strain response of 35% SiC/Ti-21S at 650 °C with fiber breakage.

Section 6 : Output and Data Visualization

The output data output in MAC/GMC 4.0 involves several levels of complexity. The simplest level of output is the data written to the MAC/GMC 4.0 output file. As illustrated in several example problems (Example 1a and 1b, for instance), this output file contains the effective properties of the composite or laminate. Detailed global field results can also be written to the output file at each time step, depending on the print level specified. The next level of complexity comes through the use of the *XYPLOT keyword. This enables generation of laminate, macro, and micro level x-y scatter plot data files containing the desired field variable components printed at each time step. These data files can then be imported or copied into plotting software (such as Microsoft Excel) to generate the desired x-y scatter plots. Many such plots (e.g., stress-strain curves) have been presented in this manual. The final (and most complex) level of results data output involves data for generating fringe plots. A fringe plot is a color-coded plot of a particular scalar field component over the composite geometry. They thus enable visualization of the spatial variation of the field component within the composite. MAC/GMC 4.0 enables output of fringe plot data through the *PATRAN and *MATLAB keywords. These keywords cause the code to write large data files containing the local fields within all of the RUC subcells at various (specified) time steps. In addition, data files containing information about the RUC geometry are generated. *PATRAN generates data files intended for post-processing with the MSC/PATRAN software package, in conjunction with the MACPOST software add-on. Note that the MACPOST software files are distributed with MAC/GMC 4.0, and that the MACPOST software has its own User Manual (Goldberg et al., 1999). *MATLAB generates data files for post-processing with the MATLAB software package. Three MATLAB source files (stress.m, strain.m, and epsp.m) are distributed with MAC/GMC 4.0 that generate fringe plots from the MATLAB data files.

This section presents three example problems dealing with the MAC/GMC 4.0 data output and visualization. Example 6a illustrates the use of the code for constructing micro (local) x-y scatter plots. Example 6b demonstrates the used of MAC/GMC 4.0 in conjunction with the MSC/PATRAN software and the MACPOST add-on to generate fringe plots. Finally, Example 6c shows how MAC/GMC 4.0 results can be used with the MATLAB software to generate fringe plots. Note that Example Problem 3f also constructed MATLAB fringe plots for both GMC and HFGMC.

Example 6a: Local x-y Plots

As illustrated in a number of the previous example problems, access is given to the MAC/GMC 4.0 local field quantities through generation of ASCII files representing data of particular subcells. This example problem exercises this micro scale x-y plot capability to show how certain micro and macro field quantities are related. The simple 2´2 square fiber, square pack RUC architecture is employed to represent a continuous 0.25 fiber volume fraction SiC/Ti-21S composite at 650 °C subjected to applied transverse strain.

MAC/GMC Input File: example_6a.mac

MAC/GMC 4.0 Example 6a - Micro x-y plots

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=2 ARCHID=1 VF=0.25 F=1 M=2

*MECH

LOP=2

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

*THERM

NPT=2 TI=0.,200. TEMP=650.,650. %

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=1. %

*PRINT

NPL=6

*XYPLOT

FREQ=5

MACRO=2

NAME=example_6a X=2 Y=8

NAME=example_6ai X=2 Y=14

MICRO=8

NAME=example_6a_11 IB=1 IG=1 X=2 Y=8

NAME=example_6a_11i IB=1 IG=1 X=2 Y=14

NAME=example_6a_12 IB=1 IG=2 X=2 Y=8

NAME=example_6a_12i IB=1 IG=2 X=2 Y=14

NAME=example_6a_21 IB=2 IG=1 X=2 Y=8

NAME=example_6a_21i IB=2 IG=1 X=2 Y=14

NAME=example_6a_22 IB=2 IG=2 X=2 Y=8

NAME=example_6a_22i IB=2 IG=2 X=2 Y=14

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: square fiber, square pack (ARCHID=1)

Fiber volume fraction: 0.25 (VF=0.25)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 2 (LOP=2)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: strain control (MODE=1)

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 650., 650. °C (TEMP=650.,650.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step sizes: 1. sec. (STP=1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

*XYPLOT

FREQ=5

MACRO=2

NAME=example_6a X=2 Y=8

NAME=example_6ai X=2 Y=14

MICRO=8

NAME=example_6a_11 IB=1 IG=1 X=2 Y=8

NAME=example_6a_11i IB=1 IG=1 X=2 Y=14

NAME=example_6a_12 IB=1 IG=2 X=2 Y=8

NAME=example_6a_12i IB=1 IG=2 X=2 Y=14

NAME=example_6a_21 IB=2 IG=1 X=2 Y=8

NAME=example_6a_21i IB=2 IG=1 X=2 Y=14

NAME=example_6a_22 IB=2 IG=2 X=2 Y=8

NAME=example_6a_22i IB=2 IG=2 X=2 Y=14

Frequency: 5 (FREQ=5)

Number of macro plots: 2 (MACRO=2)

Macro plot names: example_6a (NAME=example_6a)

example_6ai (NAME=example_6ai)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

ε₂₂, (X=2 Y=14)

Number of micro plots: 8 (MICRO=8)

Micro plot names: example_6a_11 (NAME=example_6a_11)

example_6a_11i (NAME=example_6a_11i)

example_6a_12 (NAME=example_6a_12)

example_6a_12i (NAME=example_6a_12i)

example_6a_21 (NAME=example_6a_21)

example_6a_21i (NAME=example_6a_21i)

example_6a_22 (NAME=example_6a_22)

example_6a_22i (NAME=example_6a_22i)

Micro plot subcell indices: 1, 1 (IB=1 IG=1)

1, 2 (IB=1 IG=2)

2, 1 (IB=2 IG=1)

2, 2 (IB=2 IG=2)

Micro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

ε₂₂, (X=2 Y=14)

The major difference in the data specification between micro and macro plots is, with micro plots, the subcell for which the data are to be plotted must be specified. In the present doubly periodic GMC example, the bg indices are specified. In the case of triply periodic RUC analysis, the three abg indices are specified. Finally, in the case of laminate analysis, the layer from which the subcell is taken must be specified. In addition, there are some micro scale quantities that may be specified for x-y plot file generation that cannot be specified for macro scale x-y plots (e.g., constitutive model state variables, debonding parameters). For more information on micro x-y plots, see the MAC/GMC 4.0 Keywords Manual Section 6.

7) End of file keyword: (*END)

Results

Figure 6.1 shows the RUC employed in the present example plus the bg indices of each subcell and the applied loading. Figure 6.2 is a plot of the local and global s₂₂-e₂₂ response of the SiC/Ti-21S composite. Examining the four subcell curves, the Subcell 11 curve, which is associated with the fiber, is stiff, elastic, and experiences a large local s₂₂ stress. The subcell that is in series with the fiber along the loading direction (Subcell 12) experiences the same s₂₂ stress as the fiber subcell (at a given point in time), but, since the material associated with the subcell is Ti-21S, the subcell response is more compliant and exhibits inelastic deformation. The remaining two subcells (21 and 22), which are in parallel with the fiber (with respect to the loading direction) experience far less s₂₂ stress than do subcells 11 and 12. While the s₂₂ stress is the same for subcells 21 and 22 (at a given point in time), the e₂₂ strain experienced by the subcell adjacent to the fiber (Subcell 21) is significantly higher.

A final point illustrated by Figure 6.2 involves the volume averaging of the subcell stresses and strains. As shown, if the four subcell s₂₂ stress and e₂₂ strain values are averaged in a volume-weighted sense at each point, the resulting averaged s₂₂-e₂₂ curve is identical to the macro (composite) s₂₂-e₂₂ curve plotted directly from the macro MAC/GMC 4.0 x-y plot file. The fact that the volume weighted micro stress and total strain components sum to the macro stress and total strain components is an important attribute of a micromechanics model and is often considered a consistency condition. In fact, the formulation of GMC enforces this consistency condition.

In contrast, Figure 6.3 plots the local subcell inelastic strain vs. the local total strain e₂₂. The fiber subcell (11) exhibits no inelastic strain as the fiber material is elastic. The subcells adjacent to the fiber (12 and 21) exhibit a great deal of inelastic strain, while Subcell 22 exhibits less. However, when the volume weighted average of the subcell inelastic strain values is taken at each point, the resulting curve does not correspond to the macro (composite) level curve plotted directly from the MAC/GMC 4.0 macro x-y plot file. Thus, while a consistency condition is applicable to the total strain components, such a condition does not exist for the inelastic strain components. Similarly, since the total strain is the sum of the elastic, inelastic, and thermal strains, the elastic and thermal strains do not obey a consistency condition either.

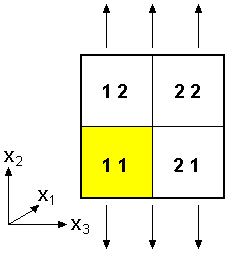
Figure 6.1 MAC/GMC 4.0 2´2 doubly periodic repeating unit cell with subcell indices identified.

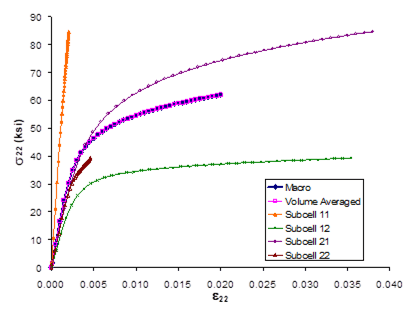
Figure 6.2 Example 6a: Macro (composite) and micro (subcell) stress-strain curves for 25% SiC/Ti-21S at 650 °C.

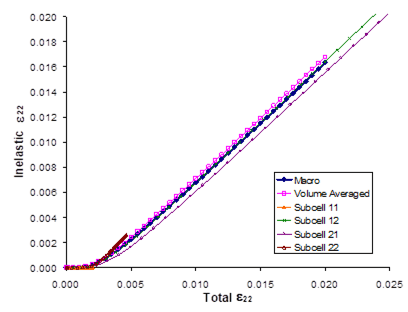
Figure 6.3 Example 6a: Macro (composite) and micro (subcell) inelastic strain vs. total strain plots for 25% SiC/Ti-21S at 650 °C.

Example 6b: PATRAN Post-Processing

This example problem demonstrates how to obtain full access to all micro and macro field data that can be produced by MAC/GMC 4.0 for use in conjunction with the MSC/PATRAN software package. This enables the generation of fringe plots, which display the spatial variation of the predicted field components over the composite geometry. The MSC/PATRAN software is available from http://www.mscsoftware.com/. In order to generate fringe plots from the MAC/GMC 4.0 software using MSC/PATRAN, an add-on to the software, known as MACPOST, is needed. MACPOST is distributed with MAC/GMC 4.0 and has its own User Manual (Goldberg et al., 1999). As indicated in the MACPOST User Manual, the add-on is capable of generating local and global x-y plots in addition to the fringe plot capabilities illustrated here. An advantage of using PATRAN to generate fringe plots is that a point can be chosen from the macro response at which to examine the micro response via fringe plots. This linkage can be used to gain some additional insight into the local mechanisms that affect the global composite response. The present example problem generates fringe plots for a triply periodic 0.25 volume fraction short fiber SiC/Ti-21S composite subjected to a stress-free cool-down followed by applied transverse strain. The evolution of the J₂ stress invariant and an inelastic strain component are displayed in the fringe plots during application of simulated transverse tensile loading.

MAC/GMC Input File: example_6b.mac

MAC/GMC 4.0 Example 6b - PATRAN post-processing

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*RUC

MOD=3 ARCHID=3 VF=0.25 ASP1=2. ASP2=1. DR=1. F=1 M=2

*MECH

LOP=2 REFTIME=57600.

NPT=3 TI=0.,57600.,57800. MAG=0.,0.,0.02 MODE=2,1

*THERM

NPT=3 TI=0.,57600.,57800. TEMP=900.,23.,23.

*SOLVER

METHOD=1 NPT=3 TI=0.,57600.,57800. STP=40.,1.

*PRINT

NPL=6

*PATRAN

TPRE=57600. STP=20

*XYPLOT

FREQ=5

MACRO=1

NAME=example_6b X=2 Y=8

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Triply periodic GMC (MOD=3)

RUC architecture: Off-set short fibers, diagonal array (ARCHID=3)

Fiber volume fraction: 0.25 (VF=0.25)

Fiber aspect ratio: 2. (ASP1=2.)

Unit cell aspect ratio: 1. (ASP2=1.)

D ratio: 1. (DR=1.)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 2 (LOP=2)

Strain reference time: 57600. sec. (REFTIME=57600.)

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600,57800.)

Load magnitude: 0., 0., 0.02 (MAG=0.,0.,0.02)

Loading mode: stress/strain control (MODE=2,1)

b) Thermal (*THERM) [KM_4]:

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600.,57800.)

Temperature points: 900., 23., 23. °C (TEMP=900.,23.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600.,57800.)

Time step sizes: 40., 1. sec. (STP=40.,1.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) PATRAN output (*PATRAN) [KM_6]:

PATRAN preloading time: 57600. sec. (TPRE=57600.)

Output step frequency: 20 (STP=20)

Two specifiers control the PATRAN output. A preloading time (TPRE) defines the time at which writing of PATRAN output begins. The output time step frequency (STP) specifies how often the PATRAN output is written. In the present example, the code writes PATRAN output every 20 time steps starting at time = 57600 sec. Thus, during the 200 time steps occurring during application of the mechanical loading, PATRAN output is written a total of 11 times.

MAC/GMC 4.0 generates 14 PATRAN output ASCII files. These 14 files are:

outfile.macgeo	RUC geometry data
outfile.total_pat.data	Number of time steps and subcells
outfile.macro1_pat.data	RUC level strain data at each output time
outfile.macro2_pat.data	RUC level stress data at each output time
outfile.macro3_pat.data	RUC level inelastic strain data at each output time
outfile.macro4_pat.data	RUC level thermal strain, creep time, temperature, and stress invariant data at each output time
outfile.micro1_pat.data	Subcell level strain data at each output time
outfile.micro2_pat.data	Subcell level stress data at each output time
outfile.micro3_pat.data	Subcell level inelastic strain data at each output time
outfile.micro4_pat.data	Subcell level thermal strain, creep time, temperature, and stress invariant data at each output time
outfile.micro1_pat.contour	Subcell level strain data for fringe plots
outfile.micro2_pat.contour	Subcell level stress data for fringe plots
outfile.micro3_pat.contour	Subcell level inelastic strain data for fringe plots
outfile.micro4_pat.contour	Subcell level thermal strain, creep time, temperature, and stress invariant data for fringe plots

where outfile is the name of the MAC/GMC 4.0 output file. In order to employ these ASCII files within PATRAN via MACPOST, all files but the first (outfile.macgeo) must be renamed. The leading “outfile.” must be stripped from the filename. For more information on the MAC/GMC 4.0 PATRAN output capabilities, see the MAC/GMC 4.0 Keywords Manual Section 6. For more information on using MACPOST, see the MACPOST User Guide (Goldberg et al., 1999).

c) x-y plots (*XYPLOT) [KM_6]:

Frequency: 5 (FREQ=5)

Number of macro plots: 1 (MACRO=1)

Macro plot names: example_6b (NAME=example_6b)

Macro plot x-y quantities: e₂₂, s₂₂ (X=2 Y=8)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Plotted in Figure 6.4 is the overall (global) transverse stress-strain response of the discontinuous SiC/Ti-21S composite considered in this example problem. Note that this plot is generated from the macro x-y plot file data. The arrows in this figure indicate the six points at which PATRAN fringe plots have been generated. Note that, although only six points have been selected, the PATRAN output files actually contain data for 11 points (i.e., fringe plots have only been generated for every other PATRAN output time).

The fringe plots generated using PATRAN with MACPOST are shown in Figure 6.5 and Figure 6.6. Figure 6.5 shows the evolution of the inelastic strain component corresponding with the direction of the applied loading (). Each of the six fringe plots shown in this figure were generated individually using the MSC/PATRAN software. Note that these fringe plots were stored as bitmap images, and some manipulation was performed beyond that of the raw PATRAN fringe plot display. Below each fringe plot, the corresponding applied global (composite level) transverse strain at which the inelastic strain component field is plotted is indicated. corresponds to the residual inelastic strain component field in the composite after the applied cool-down but before the application of any simulated mechanical loading. Note that, in this first fringe plot, the subcells that are occupied by the SiC fiber material are outlined in red. This ARCHID=3 geometry can also be seen in Figure 3.8.

Figure 6.5 indicates that during the cool-down, only the matrix subcells that are between the fibers exhibit noticeable yielding. It is not until the applied global stain reaches 0.008 that the fringe plot shows a noticeable change in the inelastic strain component field. In Figure 6.4, it is clear that this is near the point at which global yielding of the composite is occurring. As the global loading continues to increase, additional subcells yield and the inelastic strain component in the yielded subcells continues to rise. By the end of the applied loading (), all matrix subcell exhibit noticeable values, with the inelastic strain component magnitudes being highest in the matrix subcells in between the fibers along the loading direction.

Figure 6.6 shows the evolution of the J₂ stress invariant during the applied global transverse mechanical loading. The J₂ stress invariant is a von Mises type stress and is thus related to the inelastic deformation in the composite. Further, it is a scalar invariant quantity that takes into account all stress components. As the simulated mechanical loading increases, the J₂ stress increases in the composite. The highest magnitude J₂ occurs in the fibers and the matrix in between the fibers. As observed in Figure 6.5, this matrix located in between the fibers exhibits the highest magnitude as well.

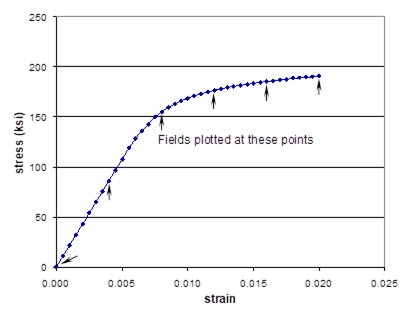
Figure 6.4 Example 6b: Simulated transverse tensile stress-strain response of 25% fiber volume fraction discontinuous SiC/Ti-21S at 23 °C. The arrows indicate the points at which the fields are plotted using the MSC/PATRAN software package in Figure 6.5 and Figure 6.6.

Figure 6.5 Example 6b: Inelastic strain component at six applied global strain levels for the 25% fiber volume fraction discontinuous SiC/Ti-21S composite at 23 °C as plotted using the MSC/PATRAN software package in conjunction with MACPOST. The fiber subcells are outlined in red in the figure for the lowest applied strain level.

Figure 6.6 Example 6b: stress invariant at six applied global strain levels for the 25% fiber volume fraction discontinuous SiC/Ti-21S composite at 23 °C as plotted using the MSC/PATRAN software package in conjunction with MACPOST. The fiber subcells are outlined in red in the figure for the lowest applied strain level.

Example 6c: MATLAB Post-Processing

This example problem demonstrates the use of MAC/GMC 4.0’s capability to generate ASCII data files that can be used to generate local fringe plots using the MATLAB software package. MATLAB is a commonly-used commercial engineering and science oriented software package (see http://www.mathworks.com/) and must be independently licensed. Three MATLAB source files are shipped with the MAC/GMC 4.0 software. These are: stress.m, strain.m, and epsp.m. These files can be used within the MATLAB software to generate fringe plots from the MAC/GMC 4.0 MATLAB ASCII files. The user is free to customize these files in order to generate the plots desired.

The present example considers a 0.35 fiber volume fraction SiC/Ti-21S composite as both a cross-ply laminate and a unidirectional composite. The 7´7 circular fiber cross-section approximation RUC architecture is employed in both cases, and loading takes the form of a stress-free cool-down. The local residual fields for the unidirectional composite and the laminate are then compared using the MATLAB software fringe plots.

MAC/GMC Input File: example_6c.mac

MAC/GMC 4.0 Example 6c - MATLAB post-processing

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

M=2 CMOD=4 MATID=A

*LAMINATE

NLY=3

LY=1 THK=0.25 ANG=0. MOD=2 ARCHID=6 VF=0.35 R=1. F=1 M=2

LY=2 THK=0.50 ANG=90. MOD=2 ARCHID=6 VF=0.35 R=1. F=1 M=2

LY=3 THK=0.25 ANG=0. MOD=2 ARCHID=6 VF=0.35 R=1. F=1 M=2

#*RUC

# MOD=2 ARCHID=6 VF=0.35 R=1. F=1 M=2

*THERM

NPT=2 TI=0.,57600. TEMP=900.,23.

*SOLVER

METHOD=1 NPT=2 TI=0.,57600. STP=40.

*PRINT

NPL=6

*MATLAB

N=1 TIMES=57600.

*XYPLOT

FREQ=40

LAMINATE=1

NAME=example_6c X=100 Y=1

MACRO=0

# MACRO=2

# NAME=example_6c_1 X=100 Y=1

# NAME=example_6c_2 X=100 Y=2

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

3) Analysis type:

Cross Ply Laminate (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 3 (NLY=3)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Aspect Ratio	Volume fraction	Fiber material	Matrix material
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(R)	(VF)	(F)	(M)
1	GMC-2D	0.25	0°	7´7 circle rect. pack	1.	0.35	SiC	Ti-21S
2	GMC-2D	0.50	90°	7´7 circle rect. pack	1.	0.35	SiC	Ti-21S
3	GMC-2D	0.25	0°	7´7 circle rect. pack	1.	0.35	SiC	Ti-21S

Unidirectional Composite (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 7´7 circle approx., rect. pack (ARCHID=6)

Fiber volume fraction: 0.35 (VF=0.35)

RUC aspect ratio: 1. (square pack) (R=1.)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

F Note: In order to execute the code for the laminate and the unidirectional composite, the appropriate lines in the input file must be commented and uncommented.

4) Loading:

a) Mechanical (*MECH): None

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 57600. sec. (TI=0.,57600.)

Temperature points: 900., 23. °C (TEMP=900.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 57600. sec. (TI=0.,57600.)

Time step sizes: 40. sec. (STP=40.)

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) MATLAB output (*MATLAB) [KM_6]:

Number of MATLAB output times: 1 (N=1)

MATLAB output times: 57600. sec. (TIMES=57600.)

As shown above, the number of times desired for writing MATLAB output, and the times themselves, must be specified. MAC/GMC 4.0 generates five MATLAB output ASCII files for RUC analysis. In the case of laminate analysis, five separate files are output for each layer. These five files are:

outfile_x2.dat ® contains x₂ direction (b) grid coordinates

outfile_x3.dat ® contains x₃ direction (g) grid coordinates

outfile_sig.dat ® contains local stresses

outfile_eps.dat ® contains local strains

outfile_epsp.dat ® contains local inelastic strains (plus material numbers)

where outfile is the name of the MAC/GMC 4.0 output file. In the case of laminate analysis, for layer numbers greater than 1, the layer number is appended to the file name root (e.g., outfile_sig_2.dat). In the case of RUC analysis, the local data for all specified TIMES is written to the same ASCII file, with the time value written prior to the data for each time. In the case of laminate analysis, the integration point number is also written on the same line as the time. The three MATLAB source files distributed with MAC/GMC 4.0 (stress.m, strain.m, and epsp.m) do not read these five ASCII files directly, rather they read the files: x2.dat, x3.dat, sig.dat, eps.dat, and epsp.dat. Thus, the ASCII files generated must be renamed. Further, the MATLAB source files only read the local data for a single time. Thus, the files sig.dat, eps.dat, and epsp.dat should contain only the local data for a single time (and integration point); the line on which the time (and integration point number) are written should not be present. For more information on the MAC/GMC 4.0 MATLAB output capabilities, see the MAC/GMC 4.0 Keywords Manual Section 6.

c) x-y plots (*XYPLOT) [KM_6]:

Frequency: 40 (FREQ=40)

Number of laminate plots: 1 (LAMINATE=1)

Laminate plot name: example_6c (NAME=example_6c)

Laminate plot x-y quantities: temperature, (X=100 Y=1)

Number of macro plots: 2 (MACRO=2)

Macro plot names: example_6c_1 (NAME=example_6c_1)

example_6c_2 (NAME=example_6c_2)

Macro plot x-y quantities: temperature, e₁₁ (X=100 Y=1)

temperature, e₂₂ (X=100 Y=2)

Number of micro plots: 0 (MICRO=0)

F Note: In the case of laminate analysis, the lines of the input file associated with the macro c-y plots must be commented. Likewise, in the case of RUC analysis, the input file lines associated with the laminate level x-y plots must be commented.

7) End of file keyword: (*END)

Results

Figure 6.7 shows the predicted global strain response of the laminate and the unidirectional composite to the imposed thermal loading. The unidirectional composite exhibits significantly more strain in the transverse (x₂) direction compared to the longitudinal (x₁) direction. The response of the cross-ply laminate is identical in both the x and y directions, and the associated curve in Figure 6.7 falls in between the two curves that represent the unidirectional composite response.

In this example problem, MATLAB data was written at the end of the cool-down, at 23 °C. The stress and inelastic strain component fields, which represent residual fields in the composite and laminate due to the imposed stress-free thermal cool-down, are plotted in Figure 6.8 and Figure 6.9. It should be noted that the x₃-direction corresponds to the through-thickness (z) direction of the laminate (see Figure 1.2). From Figure 6.8 it is apparent that the stresses are noticeably higher in the cross-ply laminate as compared to the unidirectional composite. The presence of the stiff fibers along the x and y directions in the laminate act to restrain the thermal expansion of the composite, giving rise to the larger stresses. Figure 6.9 shows that, transverse to the fiber direction (x₂ and x₃ directions), the higher stresses present in the laminate give rise to higher tensile and compressive inelastic strain concentrations in certain subcells. In the unidirectional composite, the transverse inelastic strain fields present in the x₂ and x₃ directions are identical (but rotated 90°). In the fiber (x₁) direction, on the other hand, the restraint effect of the orthogonal layers of the laminate limits the matrix inelastic strain. Thus, the overall magnitude of is lower in the laminate compared to the unidirectional composite.

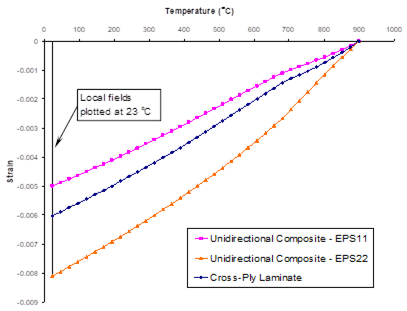
Figure 6.7 Example 6c: Predicted global response of unidirectional and cross-ply 35% SiC/Ti-21S during a stress-free cool-down.

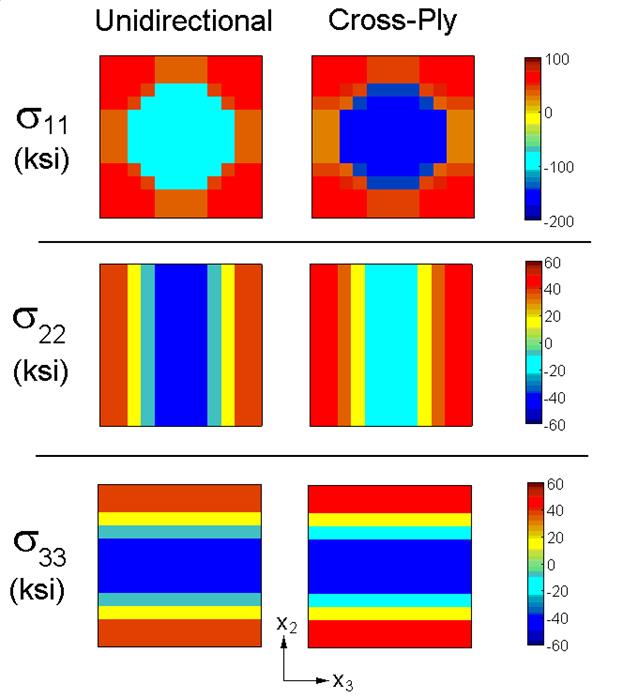
Figure 6.8 Predicted residual stress fields (plotted from MATLAB output data) for a unidirectional 35% SiC/Ti-21S composite and each ply within a cross-ply 35% SiC/Ti-21S laminate. Note that the fields in each ply of the laminate are identical in its local coordinate system.

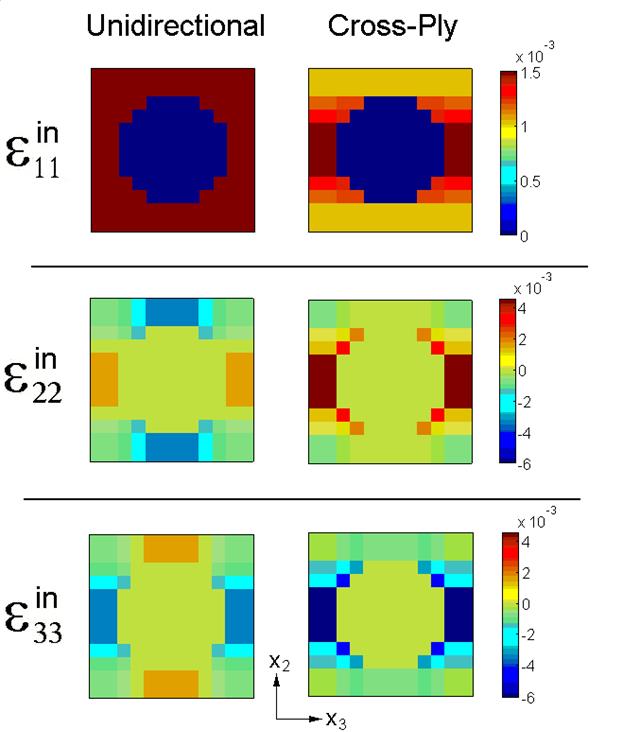
Figure 6.9 Predicted residual inelastic fields (plotted from MATLAB output data) for a unidirectional 35% SiC/Ti-21S composite and each ply within a cross-ply 35% SiC/Ti-21S laminate. Note that the fields in each ply of the laminate are identical in its local coordinate system.

Section 7 : Advanced Topics

In this Section, example problems are presented that deal with advanced topics within MAC/GMC 4.0. These advanced topics have been designated as such because they are newer to the code and thus less well established than many of the other topics dealt with in this manual. Example 7a presents the use of a new multimechanism GVIPS constitutive model. This model includes not only material viscoplastic effects, but also material viscoelastic effects. Because it employs a local tangent stiffness matrix (while globally, MAC/GMC 4.0 does not) along with a local implicit integration scheme (which is unconditionally stable), the multimechanism GVIPS model requires global equilibrium iterations (specified under the *SOLVER keyword). Non- U.S. government users of MAC/GMC 4.0 will need to obtain an additional software license in order to use the multimechanism GVIPS constitutive model.

Examples 7b and 7c present the use of the new MAC/GMC 4.0 electromagnetic analysis capabilities to analyze a smart composite material and a smart composite laminate. A good deal of additional material input data is required when the constituent materials are electromagnetically active. The final two Example Problems in this section, 7d and 7e, illustrate the analysis of woven composites using MAC/GMC 4.0. Example 7d shows a standard one step approach to the woven composite simulation, while Example 7e presents a new and more accurate two step approach.

Example 7a: Implicitly Integrated Multimechanism GVIPS

This example problem illustrates the use of a new multimechanism GVIPS constitutive model (see Saleeb et al., 2001) that has been implemented within MAC/GMC 4.0. This constitutive model incorporates an arbitrary number of viscoelastic and viscoplastic mechanisms, giving it a wide range of applicability. While this model can be characterized for any material, currently, only material parameters for Ti-21S have been implemented within MAC/GMC 4.0. The multimechanism GVIPS model has an additional distinction from the standard isotropic GVIPS model available within MAC/GMC 4.0 in that it is implicitly integrated on the local level. That is, the model, on the scale of the subcell, returns a new local stress and inelastic strain state rather than the usual local inelastic strain increments. In the standard isotropic GVIPS model available within MAC/GMC 4.0, the local inelastic strain increments returned by the constitutive model are, in contrast, explicitly integrated (to obtain inelastic strains) outside of the model itself. As discussed earlier, global equilibrium iterations are necessary at each increment of the applied simulated loading (as with the incremental plasticity model, see Example 2c).

A major benefit associated with the implicitly integrated multimechanism GVIPS model is that it is unconditionally stable, regardless of the step size employed to apply the simulated loading. Thus, unlike the previous version of GVIPS available within MAC/GMC 4.0, a very large time step size can be employed in cases that utilize this new constitutive model. This example problem illustrates this point by comparing simulations of SiC/Ti-21S composites using both GVIPS constitutive models for the Ti-21S matrix.

F Note: In order for non- U.S. government users to access the multimechanism GVIPS capabilities, an additional software license is required.

MAC/GMC Input File: example_7a.mac

MAC/GMC 4.0 Example 7a - Implicitly Integrated Multimechanism GVIPS

*CONSTITUENTS

NMATS=2

M=1 CMOD=6 MATID=E

# -- GVIPS

# M=2 CMOD=4 MATID=A

# -- Multimechanism GVIPS

M=2 CMOD=22 MATID=A

*RUC

MOD=2 ARCHID=6 VF=0.25 R=1. F=1 M=2

*MECH

LOP=2 REFTIME=57600.

NPT=3 TI=0.,57600.,57800. MAG=0.,0.,0.02 MODE=2,1

*THERM

NPT=3 TI=0.,57600.,57800. TEMP=900.,23.,23.

*SOLVER

# -- Multimechanism GVIPS Cases

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=5760.,1. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=5760.,2.5. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=5760.,4. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=5760.,8. ERR=0.001 ITMAX=100

METHOD=1 NPT=3 TI=0.,57600.,57800. STP=5760.,20. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=5760.,50. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=5760.,100. ERR=0.001 ITMAX=100

# -- GVIPS Cases

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=40.,1. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=40.,2.5 ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=40.,4. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=40.,5. ERR=0.001 ITMAX=100

# METHOD=1 NPT=3 TI=0.,57600.,57800. STP=40.,8. ERR=0.001 ITMAX=100

*PRINT

NPL=6

*XYPLOT

FREQ=1

MACRO=2

NAME=example_7a X=2 Y=8

NAME=example_7a_th X=100 Y=1

MICRO=0

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 2 (NMATS=2)

Materials: SiC fiber (MATID=E)

Ti-21S (MATID=A)

Constitutive models: SiC fiber: linearly elastic (CMOD=6)

Ti-21S matrix: Isotropic GVIPS (CMOD=4)

Multimechanism GVIPS (CMOD=22)

F Note: To generate all results in this example problem, the appropriate lines in the input file must be commented and uncommented.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Doubly periodic GMC (MOD=2)

RUC architecture: 7´7 circle approx. (ARCHID=6)

Fiber volume fraction: 0.25 (VF=0.25)

RUC aspect ratio: 1. (square pack) (R=1.)

Material assignment: SiC fiber (F=1)

Ti-21S matrix (M=2)

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: 2 (LOP=2)

Strain reference time: 57600. sec. (REFTIME=57600.)

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600,57800.)

Load magnitude: 0., 0.02 (MAG=0.,0.02)

Loading mode: stress/strain control (MODE=2,1)

b) Thermal (*THERM) [KM_4]:

Number of points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600.,57800.)

Temperature points: 900., 23., 23. (TEMP=900.,23.,23.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of time points: 3 (NPT=3)

Time points: 0., 57600., 57800. sec. (TI=0.,57600.,57800.)

Time step sizes: variable (STP=*)

Error tolerance for global iteration: 0.001 (ERR=0.001)

Maximum number of iterations: 100 (ITMAX=100)

The error tolerance (ERR) is the maximum allowable fractional difference between a global (cell or laminate level) energy increment value between iterations. Note, to generate all results presented in this example problem, the appropriate lines in the input file must be commented and uncommented. For more information on the implicitly integrated GVIPS constitutive model and its time integration control, see the MAC/GMC 4.0 Keywords Manual Sections 2 and 4 and the MAC/GMC 4.0 Theory Manual Section 4.4.3.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 6 (NPL=6)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 2 (MACRO=2)

Macro plot name: example_7a (NAME=example_7a)

example_4h_th (NAME=example_7a_th)

Macro plot x-y quantities: ε₂₂, σ₂₂ (X=2 Y=8)

temperature, ε₁₁ (X=100 Y=1)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Figure 7.1 shows the simulated transverse tensile response of the SiC/Ti-21S composite wherein the standard isotropic GVIPS constitutive model (CMOD=4) has been employed to represent the matrix. As this model is explicitly integrated in time, a small time step is required in order to achieve convergence. Figure 7.1 illustrates the effect of using a successively coarser time step to apply the 0.02 global transverse strain over 200 seconds. Convergence is achieved for time step sizes of 1 and 2.5 seconds, but for a time step of 4 seconds, some oscillations are present in the simulated stress-strain curve. These oscillations become more apparent for a time step of 5 seconds. Finally, for a time step of 8 seconds, the solution diverges (causing the code to fail).

Figure 7.2 shows the same simulations for the SiC/Ti-21S composite, but now the new implicitly integrated multimechanism GVIPS constitutive model (CMOD=22) has been employed for the matrix. Employing a time step up to and including 20 seconds allows the simulated stress-strain curve to be well represented without divergence or oscillations. A time step size of 50 seconds still does a reasonable job of reproducing the stress-strain curve predicted using much finer time step sizes. Finally, using a time step size of 100 seconds (which applies the entire simulated load in just 2 steps) the integration still achieves convergence. Note that even though the intermediate point on this simulated stress-strain curve does fall significantly outside the previous predictions, the ending stress (at an applied strain of 0.02) is still within 3.5 % of the previously predicted stress levels. Also, it is important to remember that the global equilibrium iterations required in the case of the multimechanism GVIPS model adds additional overhead to the code’s execution. Thus, to preserve the code’s efficiency, a relatively large time step should be employed when using the multimechanism GVIPS model.

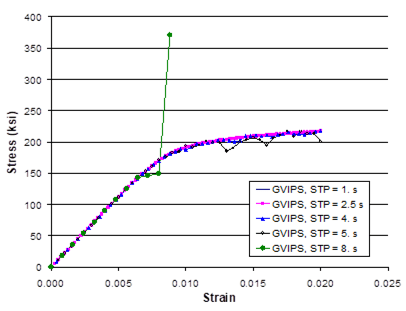
Figure 7.1 Example 7a: Simulated transverse tensile response of 25% SiC/Ti-21S at room temperature wherein the Ti-21S matrix response is simulated using the standard isotropic GVIPS constitutive model. Effect of the loading time step size is highlighted.

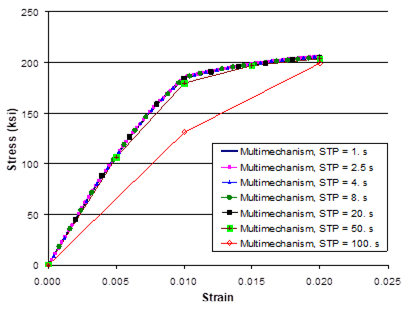
Figure 7.2 Example 7a: Simulated transverse tensile response of 25% SiC/Ti-21S at room temperature wherein the Ti-21S matrix response is simulated using the new implicitly integrated multimechanism GVIPS constitutive model. Effect of the loading time step size is highlighted.

Example 7b: Electromagnetic RUC Analysis

This example problem involves the use of the new electromagnetic micromechanics capabilities within MAC/GMC 4.0. The basic difference between standard and electromagnetic micromechanics involves the form of the material constitutive equation employed. In the standard micromechanics constitutive equations, stresses and strains are related by the stiffness matrix. In electromagnetic micromechanics, the constitutive equations are expanded,

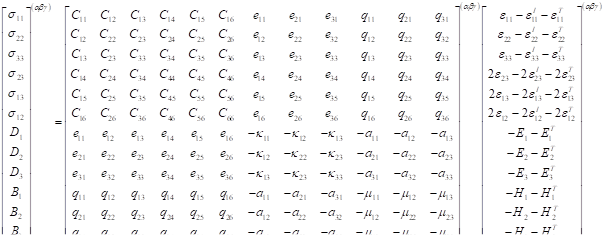
where are the stress components, are the electric displacement components, are the magnetic flux density components, are the total strain components, are the inelastic strain components, are the thermal strain components, are the electric field components, are the thermo-electric field components, are the magnetic field components, are the thermo-magnetic field components, are the material stiffness components, are the material piezoelectric components, are the material piezomagnetic components, are the material dielectric components, are the material magnetoelectric components, and are the material magnetic permeability components of a given subcell (denoted by the indices ). The thermal strain and thermal field components are related to a change in temperature from a given reference temperature (i.e., ) by,

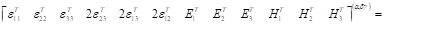
where are the subcell material coefficients of thermal expansion (CTEs), are the subcell material pyroelectric constants, and are the subcell material pyromagnetic constants.

For the truly anisotropic case described by the above constitutive equation, there are indeed a great number of additional terms that must be known to characterize a material’s electromagnetic response. Fortunately, in practice, a great number of the coefficients in the stiffness/electromagnetic coefficient matrix are zero. MAC/GMC 4.0 admits electromagnetic materials of class C_6v with an arbitrary poling direction. These types of materials are in many ways analogous to transversely isotropic materials. Assuming an x₁ poling direction, the above equations reduce to,

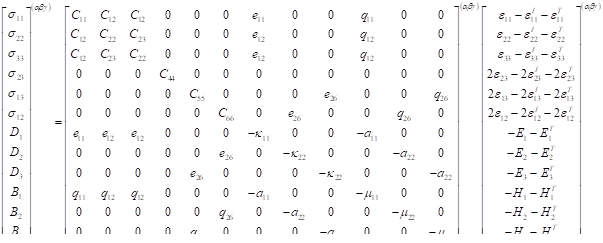
Thus, in addition to the standard thermo-mechanical material coefficients, for an electromagnetic material, the additional material parameters are: three piezoelectric parameters (e₁₁, e₁₂, e₂₆), three piezomagnetic parameters (q₁₁, q₁₂, q₂₆), two dielectric parameters (k₁₁, k₂₂), two magnetoelectric parameters (a₁₁, a₁₂), two magnetic permeability parameters (m₁₁, m₂₂), two pyroelectric parameters (z₁, z₂), and two pyromagnetic parameters (y₁, y₂), for a total of sixteen additional material parameters. In MAC/GMC 4.0, these parameters are read directly from the input file for an assumed x₁ poling direction. However, thanks to MAC/GMC 4.0’s transversely isotropic elastic constitutive model that allows an arbitrary direction of transverse isotropy, the actual poling direction of the material is arbitrary.

The present example problem considers a particulate composite consisting of a BaTiO₃ (barium titanate) inclusion and a CoFe₂O₄ (cobalt ferrite) matrix. The BaTiO₃ is a piezoelectric material (non-zero e_ij parameters), while the CoFe₂O₄ is a piezomagnetic material (non-zero q_ij terms). When combined to form a composite, the resulting BaTiO₃/CoFe₂O₄ material is electromagnetic. Composites with one or more piezoelectric or electromagnetic phases are often referred to as “smart composites”. The smart composite is subjected to strain-controlled loading at 24 °C.

MAC/GMC Input File: example_7b.mac

MAC/GMC 4.0 Example 7b - Electromagnetic RUC analysis

*ELECTROMAG

*CONSTITUENTS

NMATS=2

# -- BaTiO3 (Barium Titanate)

M=1 CMOD=9 MATID=U MATDB=1 EM=1

NTP=2

TEM=24.,600.

EA=111.93E9,111.93E9

ET=116.33E9,116.33E9

NUA=0.321,0.321

NUT=0.307,0.307

GA=43.0E9,43.0E9

ALPA=1.99E-6,1.99E-6

ALPT=8.53E-6,8.53E-6

D=0.,0.,1.

ES11=18.6,18.6

ES12=-4.4,-4.4

ES26=11.6,11.6

QS11=0.0,0.0

QS12=0.0,0.0

QS26=0.0,0.0

KS11=12.6E-9,12.6E-9

KS22=11.2E-9,11.2E-9

AS11=0.0,0.0

AS22=0.0,0.0

MS11=10.0E-6,10.0E-6

MS22=5.0E-6,5.0E-6

PELS1=0.13E5,0.13E5

PELS2=0.13E5,0.13E5

PMGS1=0.0,0.0

PMGS2=0.0,0.0

# -- CoFe2O4 (Cobalt Ferrite)

M=2 CMOD=9 MATID=U MATDB=1 EM=1 &

EL=143.57E9,154.57E9,0.37,0.368,45.3E9,0.00E-6,0.00E-6 &

D=0.,0.,1.

ES=0.0,0.0,0.0

QS=699.7,580.3,550.

KS=0.93E-10,0.08E-9

AS=0.0,0.0

MS=157.E-6,-590.E-6

PELS=0.0,0.0

PMGS=0.0,0.0

*RUC

MOD=3 ARCHID=1 VF=0.25 ASP=1. F=1 M=2

*MECH

LOP=99

NPT=2 TI=0.,200. MAG=0.,0. MODE=2

NPT=2 TI=0.,200. MAG=0.,0.02 MODE=1

NPT=2 TI=0.,200. MAG=0.,0. MODE=2

*THERM

NPT=2 TI=0.,200. TEMP=24.,24.

*SOLVER

METHOD=1 NPT=2 TI=0.,200. STP=100.

*PRINT

NPL=8

*XYPLOT

FREQ=1

MACRO=2

NAME=example_7b_se X=3 Y=9

NAME=example_7b_De X=3 Y=46

NAME=example_7b_Be X=3 Y=49

MICRO=0

*END

Annotated Input Data

1) Flags:

a) Perform electromagnetic analysis (*ELECTROMAG) [KM_1]:

2) Constituent materials (*CONSTITUENTS) [KM_2]:

*CONSTITUENTS

NMATS=2

# -- BaTiO3 (Barium Titanate)

M=1 CMOD=9 MATID=U MATDB=1 EM=1

NTP=2

TEM=24.,600.

EA=111.93E9,111.93E9

ET=116.33E9,116.33E9

NUA=0.321,0.321

NUT=0.307,0.307

GA=43.0E9,43.0E9

ALPA=1.99E-6,1.99E-6

ALPT=8.53E-6,8.53E-6

D=0.,0.,1.

ES11=18.6,18.6

ES12=-4.4,-4.4

ES26=11.6,11.6

QS11=0.0,0.0

QS12=0.0,0.0

QS26=0.0,0.0

KS11=12.6E-9,12.6E-9

KS22=11.2E-9,11.2E-9

AS11=0.0,0.0

AS22=0.0,0.0

MS11=10.0E-6,10.0E-6

MS22=5.0E-6,5.0E-6

PELS1=0.13E5,0.13E5

PELS2=0.13E5,0.13E5

PMGS1=0.0,0.0

PMGS2=0.0,0.0

Number of materials: 2 (NMATS=2)

Constitutive model: Arbitrary transversely isotropic (CMOD=9)

Materials: User-Defined (MATID=U)

Material property source: Read from input file (MATDB=1)

Electromagnetic specifier: Material is electromagnetic (EM=1)

F Note: Electromagnetic analysis requires that the material properties be specified by the user in the MAC/GMC 4.0 input file. The electromagnetic specifier indicates whether or not the particular material has electromagnetic properties (EM=0 indicated that the material does not have electromagnetic properties). Further, the arbitrary transversely isotropic elastic constitutive model (CMOD=9) must be employed.

For illustrative purposes, the material properties for the barium titanate material have been input as temperature-dependent (although the same material properties are employed for each input temperature). As indicated, the sixteen additional material parameters are specified for the two input temperatures. ES11, ES12, and ES26 are the three piezoelectric parameters, QS11, QS12, and QS26 are the three piezomagnetic parameters, KS11 and KS22 are the two magnetoelectric parameters, AS11 and AS22 are the two magnetoelectric parameters, and MS11 and MS22 are the two magnetic permeability parameters. PELS1 and PELS2 correspond to the two pyroelectric parameters (z₁, z₂), while PMGS1 and PMGS2 correspond to the two pyromagnetic parameters (y₁, y₂). In addition, a direction vector (D=0.,0.,1.) has been specified. This direction vector is standard input associated with the arbitrary transversely isotropic elastic constitutive model (CMOD=9). It specifies the direction of transverse isotropy with respect to the RUC coordinate axes (i.e., it specifies the vector that is normal to the plane of transverse isotropy) (see the MAC/GMC 4.0 Keywords Manual Section 2). When employed in conjunction with electromagnetic analysis, the direction vector also specifies the poling direction for the electromagnetic material. Thus, in the present case, an x₃ poling direction has been specified for the materials.

# -- CoFe2O4 (Cobalt Ferrite)

M=2 CMOD=9 MATID=U MATDB=1 EM=1 &

EL=143.57E9,154.57E9,0.37,0.368,45.3E9,0.00E-6,0.00E-6 &

D=0.,0.,1.

ES=0.0,0.0,0.0

QS=699.7,580.3,550.

KS=0.93E-10,0.08E-9

AS=0.0,0.0

MS=157.E-6,-590.E-6

PELS=0.0,0.0

PMGS=0.0,0.0

For the cobalt ferrite material, temperature-independent material properties have been input. The ordering for the electromagnetic material parameter input is intuitive. For more information on the electromagnetic material parameter specification, see the MAC/GMC Keywords Manual Section 2.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Triply periodic GMC (MOD=3)

RUC architecture: short fiber, square array (ARCHID=1)

Fiber volume fractions: 0.25 (VF=0.25)

Fiber aspect ratio 1. (ASP=1.)

Material assignment: BaTiO₃ (barium titanate) fiber (F=1)

CoFe₂O₄ (cobalt ferrite) matrix (M=2)

F Note: Electromagnetic analysis requires use of a triply periodic RUC (MOD=3).

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: general loading (LOP=99)

Component #1 (e₁₁ or s₁₁)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #2 (e₂₂ or s₂₂)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #3 (e₃₃ or s₃₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.02
Control (MODE=)		strain

Component #4 (g₂₃ or s₂₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #5 (g₁₃ or s₁₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #6 (g₁₂ or s₁₂)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		stress

Component #7 (E₁ or D₁)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		electric displacement (D₁)

Component #8 (E₂ or D₂)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		electric displacement (D₂)

Component #9 (E₃ or D₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		electric displacement (D₃)

Component #10 (H₁ or B₁)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		magnetic flux density (B₁)

Component #11 (H₂ or B₂)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		magnetic flux density (B₂)

Component #12 (H₃ or B₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		200.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		magnetic flux density (B₃)

For electromagnetic analysis, the general loading option must be selected. Further, there are now six additional load components that may be applied to the composite: three components of electric displacement or electric field and three components of magnetic flux density or magnetic field. The present case simulates application of strain in the x₃-direction to a composite that is otherwise free of loading. As usual, these “free” loading conditions take the form of zero applied global stresses for all components other than the normal 33 component. The non-loaded strain components are permitted to arise naturally. In terms of electromagnetic effects, “free” loading conditions correspond to zero applied electrical displacement and magnetic flux density (rather than zero applied electric and magnetic field components). The electric and magnetic field components are permitted to arise naturally. For more information on loading specification for electromagnetic analysis, see the MAC/GMC Keywords Manual Section 4.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Temperature points: 24., 24. (TEMP=24.,24.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 200. sec. (TI=0.,200.)

Time step size: 100. sec. (STP=100)

F Note: Since this problem is linear electro-magneto-elastic, the time step size is unimportant in terms of convergence.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 8 (NPL=8)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 1 (FREQ=1)

Number of macro plots: 3 (MACRO=3)

Macro plot name: example_7b_se (NAME=example_7b_se)

example_7b_De (NAME=example_7b_De)

example_7b_Be (NAME=example_7b_Be)

Macro plot x-y quantities: ε₃₃, σ₃₃ (X=3 Y=9)

ε₃₃, D₃ (X=3 Y=46)

ε₃₃, B₃ (X=3 Y=49)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

Since the particulate BaTiO₃/CoFe₂O₄ electromagnetic (smart) composite considered in this example problem consists of phases that are both linear electro-magneto-elastic, results in the form of effective properties (from the MAC/GMC 4.0 output file) will be examined. First, consider the effective (global) electro-magneto-elastic matrix for the smart composite:

ZG - Effective/Macro Stiffness/Electromagnetic Coefficient Matrix

| 2.449D+11 1.382D+11 1.353D+11 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 -1.565D-02 0.000D+00 0.000D+00 3.078D+02 |

| 1.382D+11 2.449D+11 1.353D+11 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 -1.565D-02 0.000D+00 0.000D+00 3.078D+02 |

| 1.353D+11 1.353D+11 2.404D+11 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 9.518D-02 0.000D+00 0.000D+00 3.861D+02 |

| 0.000D+00 0.000D+00 0.000D+00 4.733D+10 0.000D+00 0.000D+00 0.000D+00 4.891D-02 0.000D+00 0.000D+00 3.397D+02 0.000D+00 |

| 0.000D+00 0.000D+00 0.000D+00 0.000D+00 4.733D+10 0.000D+00 4.891D-02 0.000D+00 0.000D+00 3.397D+02 0.000D+00 0.000D+00 |

| 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 5.306D+10 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 |

| 0.000D+00 0.000D+00 0.000D+00 0.000D+00 4.891D-02 0.000D+00 -1.332D-10 0.000D+00 0.000D+00 2.179D-10 0.000D+00 0.000D+00 |

| 0.000D+00 0.000D+00 0.000D+00 4.891D-02 0.000D+00 0.000D+00 0.000D+00 -1.332D-10 0.000D+00 0.000D+00 2.179D-10 0.000D+00 |

| -1.565D-02 -1.565D-02 9.518D-02 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 -1.547D-10 0.000D+00 0.000D+00 -1.210D-11 |

| 0.000D+00 0.000D+00 0.000D+00 0.000D+00 3.397D+02 0.000D+00 2.179D-10 0.000D+00 0.000D+00 3.517D-04 0.000D+00 0.000D+00 |

| 0.000D+00 0.000D+00 0.000D+00 3.397D+02 0.000D+00 0.000D+00 0.000D+00 2.179D-10 0.000D+00 0.000D+00 3.517D-04 0.000D+00 |

| 3.078D+02 3.078D+02 3.861D+02 0.000D+00 0.000D+00 0.000D+00 0.000D+00 0.000D+00 -1.210D-11 0.000D+00 0.000D+00 -1.011D-04 |

This matrix relates the global stress/electric displacement/magnetic flux density vector to the global strain/electric field/magnetic field vector, and is of identical form to that of each phase as shown in the local constitutive equation given earlier in this example problem. The composite, like the barium titanate inclusion, has non-zero piezoelectric parameters (e_ij). In addition, like the cobalt ferrite matrix, the composite has non-zero piezomagnetic parameters (q_ij). Most interesting, however, is the fact that the smart composite has non-zero magnetoelectric parameters (a_ij), whereas the a_ij of each constituent is zero. These magnetoelectric parameters provide coupling between the electric and magnetic effects in the composite. That is, for instance, when this coupling is present, electric displacement components can arise due to an applied magnetic field. It is noteworthy that the smart composite exhibits this electro-magnetic coupling when neither constituent does.

Next, the effective engineering properties of the smart composite, along with the thermal coefficients, are output:

Effective Engineering Moduli

E11S= 0.1459E+12

N12S= 0.3679

E22S= 0.1459E+12

N23S= 0.3557

E33S= 0.1449E+12

G23S= 0.4733E+11

G13S= 0.4733E+11

G12S= 0.5306E+11

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.1927E-05 0.1927E-05 0.3256E-06

0.3074E-08 0.3074E-08 0.0000E+00

Effective Pyroelectric Vector

0.5223E+04 0.5223E+04 0.6427E+04

Effective Pyromagnetic Vector

-0.1131E-02 -0.1131E-02 0.2688E+01

Here again, the electromagnetic coupling gives rise to interesting effects in the smart composite that are absent in both of the constituents. First of all, shear coefficients of thermal expansion arise in the composite. This indicates that in response to an applied temperature change, global shear strain will result in the composite. Further, while the pyromagnetic parameters for each constituent are zero, the composite has non-zero pyromagnetic parameters. Thus, thermo-magnetic field components () will arise in the smart composite due to applied thermal loading even though this would not occur in either of the monolithic constituents.

Finally, the present example problem involved application of a global normal strain to the smart composite. The time-based output written to the MAC/GMC 4.0 output file includes:

2 TIME: 2.0000D+02 TEMP: 2.4000D+01 TSTEP: 1.0000D+02

-----------------------------------------------------------------------------------------------

STRESS: 0.0000D+00 0.0000D+00 2.9041D+09 0.0000D+00 0.0000D+00 0.0000D+00

E-M FLUX: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

STRAIN: -7.0886D-03 -7.0886D-03 2.0000D-02 0.0000D+00 0.0000D+00 0.0000D+00

E-M FIELD: 0.0000D+00 0.0000D+00 -1.3739D+07 0.0000D+00 0.0000D+00 -3.3223D+04

TH. STRAIN: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

PYRO E-M FIELD: 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00 0.0000D+00

TANGENT CTE: 1.9274D-06 1.9274D-06 3.2555D-07 3.0735D-09 3.0735D-09 0.0000D+00

SECANT CTE: 1.9274D-06 1.9274D-06 3.2555D-07 3.0735D-09 3.0735D-09 0.0000D+00

TAN PYRO E-M VECT: 5.2231D+03 5.2231D+03 6.4268D+03 -1.1308D-03 -1.1308D-03 2.6880D+00

SEC PYRO E-M VECT: 5.2231D+03 5.2231D+03 6.4268D+03 -1.1308D-03 -1.1308D-03 2.6880D+00

NOTE: TREF = 24.000

Thus, in response to the applied normal strain loading (e₃₃), the composite experiences the standard mechanical response (non-zero s₃₃, e₁₁, and e₂₂), in addition to a non-zero electric field component (E₃ = -1.3739´10⁷ V/m) and a non-zero magnetic field component (H₃ = -3.3223´10⁴ A/m). The S.I. units for the electric field (E_k) are volts per meter (V/m) or Newtons per Coulomb (N/C) and for magnetic field (H_k), the S.I. units are Amperes per meter (A/m). The S.I units for electric displacement (D_k) are Coulombs per square meter (C/m²) and for magnetic flux density (B_k), the S.I. units are Newtons per Ampere-meter (N/Am). For additional information on electromagnetic analysis with MAC/GMC 4.0, see the MAC/GMC 4.0 Keywords Manual Section 2.

Finally, the local electric and magnetic field components that are induced in the BaTiO₃/CoFe₂O₄ composite are shown in Figure 7.3. A relatively constant electric field is induced while the induce magnetic field varies widely in the composite.

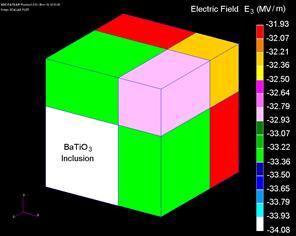
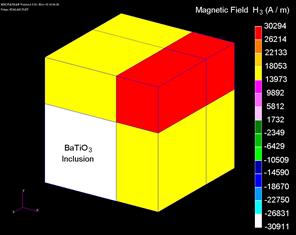
Figure 7.3 Example 7b: Local electric field component E₃ and magnetic field component H₃ induced in the smart BaTiO₃/CoFe₂O₄ composite by an applied global strain of.

Example 7c: Electromagnetic Laminate Analysis

This example problem considers an electromagnetic (smart) composite laminate. In particular, a hybrid smart/metal matrix composite laminate is analyzed consisting of a unidirectional B/Al layer sandwiched between two BaTiO₃/CoFe₂O₄ layers (see Figure 7.4). By reversing the electromagnetic polarity of the bottom smart composite layer, a completely different laminate response can be obtained. The applied loading involves a through-thickness magnetic field component.

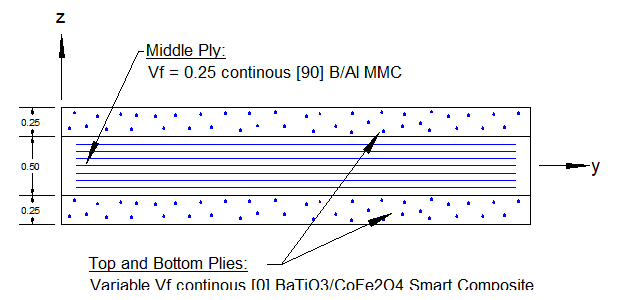
Figure 7.4 Hybrid smart/MMC laminate analyzed in MAC/GMC 4.0 Example Problem 7c.

MAC/GMC Input File: example_7c.mac

MAC/GMC 4.0 Example 7c - Electromagnetic laminate analysis

*ELECTROMAG

*CONSTITUENTS

NMATS=5

# -- BaTiO3 (Barium Titanate)

M=1 CMOD=9 MATID=U MATDB=1 EM=1 &

EL=111.93E9,116.33E9,0.321,0.307,43.0E9,1.99E-6,8.53E-6 &

D=1.,0.,0.

ES=18.6,-4.4,11.6

QS=0.0,0.0,0.0

KS=12.6E-9,11.2E-9

AS=0.0,0.0

MS=10.0E-6,5.0E-6

PELS=0.13E5,0.13E5

PMGS=0.0,0.0

# -- CoFe2O4 (Cobalt Ferrite) - positive poling direction

M=2 CMOD=9 MATID=U MATDB=1 EM=1 &

EL=143.57E9,154.57E9,0.37,0.368,45.3E9,0.00E-6,0.00E-6 &

D=0.,0.,1.

ES=0.0,0.0,0.0

QS=699.7,580.3,550.

KS=0.93E-10,0.08E-9

AS=0.0,0.0

MS=157.E-6,-590.E-6

PELS=0.0,0.0

PMGS=0.0,0.0

# -- CoFe2O4 (Cobalt Ferrite) - negative poling direction

M=3 CMOD=9 MATID=U MATDB=1 EM=1 &

EL=143.57E9,154.57E9,0.37,0.368,45.3E9,0.00E-6,0.00E-6 &

D=0.,0.,-1.

ES=0.0,0.0,0.0

QS=699.7,580.3,550.

KS=0.93E-10,0.08E-9

AS=0.0,0.0

MS=157.E-6,-590.E-6

PELS=0.0,0.0

PMGS=0.0,0.0

# -- Boron

M=4 CMOD=6 MATID=U MATDB=1 EM=0 &

EL=400.E9,400.E9,0.20,0.20,166.6667E9,8.3E-6,8.3E-6

# -- Aluminum

M=5 CMOD=1 MATID=U MATDB=1 EM=0 &

EL=72.6E9,72.6E9,0.33,0.33,72.283E9,22.5E-6,22.5E-6 &

VI=1.E4,65.E6,150.E6,50.,10.,1.

*LAMINATE

NLY=3

LY=1 THK=0.25 ANG=0. MOD=3 ARCHID=99 EM=1

NA=1 NB=2 NG=2

D=1.

H=0.5,0.5

L=0.5,0.5

SM=1,2

SM=2,2

LY=2 THK=0.5 ANG=90. MOD=2 ARCHID=1 VF=0.25 F=4 M=5 EM=0

LY=3 THK=0.25 ANG=0. MOD=3 ARCHID=99 EM=1

NA=1 NB=2 NG=2

D=1.

H=0.5,0.5

L=0.5,0.5

SM=1,2

SM=2,2

# SM=1,3

# SM=3,3

*MECH

LOP=99

NPT=2 TI=0.,600. MAG=0.,0. MODE=2

NPT=2 TI=0.,600. MAG=0.,0. MODE=1

NPT=2 TI=0.,600. MAG=0.,0. MODE=2

NPT=2 TI=0.,600. MAG=0.,0. MODE=1

NPT=2 TI=0.,600. MAG=0.,6.E6 MODE=1

*THERM

NPT=2 TI=0.,600. TEMP=24.,24.

*SOLVER

METHOD=1 NPT=2 TI=0.,600. STP=0.25

*PRINT

NPL=8

*XYPLOT

FREQ=40

LAMINATE=5

NAME=example_7c_ex X=34 Y=1

NAME=example_7c_ey X=34 Y=2

NAME=example_7c_ez X=34 Y=3

NAME=example_7c_kx X=34 Y=7

NAME=example_7c_ky X=34 Y=8

MACRO=0

MICRO=0

*END

Annotated Input Data

1) Flags:

a) Perform electromagnetic analysis (*ELECTROMAG) [KM_1]:

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 5 (NMATS=5)

Materials: User-Defined (MATID=U)

Constitutive models: Arbitrary transversely isotropic (CMOD=9)

Linearly elastic (CMOD=6)

Bodner-Partom (CMOD=1)

Material property source: Read from input file (MATDB=1)

Electromagnetic specifier: Material is elecromagnetic (EM=1)

Material is not elecromagnetic (EM=0)

The boron and aluminum materials are specified with EM=0 to indicate that they do not have electromagnetic properties associated with them. The cobalt ferrite material properties are specified twice – each time with a different direction vector. Since the direction vector is a material property, the same material with only a change in direction vector constitutes a new material. In the present case, the sign of the direction vector of the cobalt ferrite is reversed. While this has no effect on the mechanical properties, it causes a sign reversal in the material’s electromagnetic properties.

3) Analysis type (*LAMINATE) ® Laminate Analysis [KM_3]:

Number of layers: 3 (NLY=3)

Layer	Analysis Model	Thickness	Fiber Angle	Architecture	Volume fraction	Fiber material	Matrix material	E-M Specifier
(LY=)	(MOD)	(THK)	(ANG)	(ARCHID)	(VF)	(F)	(M)	(EM)
1	GMC-3D	0.25	90°	short fiber square array	0.25	BaTiO₃	CoFe₂O₄	electro-magnetic
2	GMC-2D	0.50	0°	short fiber square array	0.25	boron	aluminum	not electro-magnetic
3	GMC-3D	0.25	90°	short fiber square array	0.25	BaTiO₃	CoFe₂O₄	Electro-magnetic

For electromagnetic laminate analysis, there is an additional piece of information required for each layer that specifies whether or not the layer is electromagnetic. EM=1 indicates that the layer is electromagnetic, while EM=0 indicates that the layer is not electromagnetic.

F Note: To generate the results for the magnetically asymmetric laminate, the appropriate lines in the input file must be commented and uncommented.

4) Loading:

a) Mechanical (*MECH) [KM_4]:

Loading option: general loading (LOP=99)

Component #1 ( or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		force resultant

Component #2 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		force resultant

Component #3 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.02
Control (MODE=)		force resultant

Component #4 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		moment resultant

Component #5 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		moment resultant

Component #6 (or )

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		moment resultant

Component #7 (E₁)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		electric field (E₁)

Component #8 (E₂)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		electric field (E₂)

Component #9 (E₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		electric field (E₃)

Component #10 (H₁)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		magnetic field (H₁)

Component #11 (H₂)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		0.
Control (MODE=)		magnetic field (H₂)

Component #12 (H₃)

Number of points: 2 (NPT=2)

Times (TI=) (sec.)	0.		600.
Magnitudes (MAG=)	0.		6,000,000 A/m
Control (MODE=)		magnetic field (H₃)

F Note: Currently, in the case of an electromagnetic laminate, only electromagnetic field components (E_k and H_k) may be applied. The electromagnetic lamination theory does not admit application of laminate level electric displacements (D_k) or magnetic flux density componenents (B_k), although average laminate electric displacements and magnetic flux densities can arise. For more information on loading specification for electromagnetic analysis, see the MAC/GMC Keywords Manual Section 4.

b) Thermal (*THERM) [KM_4]:

Number of points: 2 (NPT=2)

Time points: 0., 600. sec. (TI=0.,600.)

Temperature points: 24., 24. (TEMP=24.,24.)

c) Time integration (*SOLVER) [KM_4]:

Time integration method: Forward Euler (METHOD=1)

Number of points: 2 (NPT=2)

Time points: 0., 600. sec. (TI=0.,600.)

Time step size: 0.25 sec. (STP=0.25)

F Note: Unlike Example Problem 7b, this example problem contains an inelastic material (aluminum). Thus, a small time step must be employed to achieve convergence.

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: 8 (NPL=8)

b) x-y plots (*XYPLOT) [KM_6]:

Frequency: 40 (FREQ=40)

Number of laminate plots: 5 (LAMINATE=5)

Laminate plot name: example_7c_ex (NAME=example_7c_ex)

example_7c_ey (NAME=example_7c_ey)

example_7c_ez (NAME=example_7c_ez)

example_7c_kx (NAME=example_7c_kx)

example_7c_ky (NAME=example_7c_ky)

Laminate plot x-y quantities: H_z, (X=34 Y=1)

H_z, (X=34 Y=2)

H_z, (X=34 Y=3)

H_z, (X=34 Y=7)

H_z, (X=34 Y=8)

Number of macro plots: 0 (MACRO=0)

Number of micro plots: 0 (MICRO=0)

7) End of file keyword: (*END)

Results

This example problem highlights the effect of reversing the magnetic polarity of the CoFe₂O₄ in one of the BaTiO₃/CoFe₂O₄ layers in the hybrid smart/MMC laminate. First, for the case in which the poling direction of both 0° BaTiO₃/CoFe₂O₄ layers is the x₃-direction (laminate z-direction), the laminate responds to the applied through-thickness magnetic field with extension (midplane strains), but no curvature. The midplane strain response of the magnetically symmetric laminate is plotted in Figure 7.5. Also plotted is the average through-thickness strain in the laminate. The laminate exhibits more midplane strain in the x-direction than the y-direction because the continuous and stiff boron fibers of the middle 90° layer are oriented in the y-direction. The out-of-plane strain is of the largest magnitude because of the large effect piezomagnetic term q₃₃ of the smart plies. It is clear from the knees in the curves plotted in Figure 7.5 the point at which yielding commences in the B/Al ply. The MAC/GMC 4.0 output file confirms that, in addition to non-zero magnetic force resultants, non-zero inelastic force resultants arise in the laminate. It should be noted that, in addition to the strains, the laminate experiences an average electric displacement component, D_x, and an average magnetic flux component B_z.

When the poling direction of the CoFe₂O₄ in the bottom 0° BaTiO₃/CoFe₂O₄ layer is reversed, the laminate responds to the applied through-thickness magnetic field in a completely different way. As shown in Figure 7.6, this magnetically asymmetric laminate responds with curvature but no midplane extension. The reversal in poling direction causes a reversal of the sign of the effective q_ij and a_ij terms for the bottom smart composite layer; the signs are now opposite of those in the top smart composite layer, causing the magnetic asymmetry. As a result, magnetic moment resultants, rather than force resultants, arise in the composite due to the applied magnetic field. An identical average magnetic flux component, B_z arises in the magnetically asymmetric laminate, but the average electric displacement component, D_x, that was present in the magnetically symmetric laminate, is now zero. Note that, mechanically, the two laminates are identical, with identical ABD matrices. A slight knee is present in the curves of Figure 7.6, but the effect of the B/Al ply inelasticity is much smaller than in the magnetically symmetric laminate. The magnitude of the curvature is smaller in the y-direction than the x-direction due to the stiff boron fibers oriented along the y-direction.

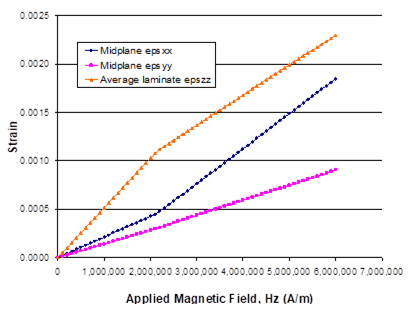
Figure 7.5 Example 7c: Strain response of a symmetric [0°/90°]_s hybrid smart/MMC laminate to an applied through-thickness magnetic field.

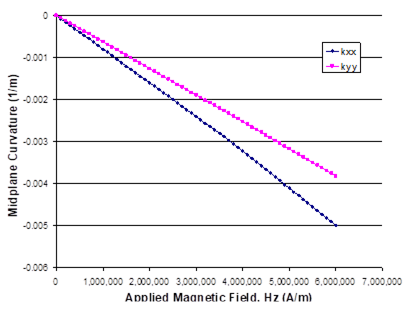
Figure 7.6 Example 7c: Curvature response of a magnetically asymmetric [0°/90°]_s hybrid smart/MMC laminate to an applied through-thickness magnetic field.

Example 7d: Woven Composite Analysis – Single Step

This example problem and the next illustrate MAC/GMC 4.0’s ability to analyze composites with woven (or braided) reinforcements. The present example problem performs the analysis using a one step homogenization procedure. The next example problem uses a two step procedure that gives improved results. Triply periodic GMC has the ability to represent the inherently three-dimensional architecture of the reinforcement in woven composites. Currently, woven composites may be treated within MAC/GMC 4.0 by employing the internal constitutive models that allow specification of an arbitrary direction of transverse isotropy (CMOD= 3, 7, or 9). Then, by choosing the direction vector appropriately for the material occupying each subcell, the woven reinforcement architecture can be represented.

Woven polymer matrix composites (PMCs), such as graphite/epoxy, are a common type of woven composite. The polymer matrix in these composites is often treated as linearly elastic. An important class of woven PMC is considered in this example problem: plain weave reinforced PMCs. The plain weave architecture involves fibers, or more commonly tows of fibers, in a repeating over-one, under-one pattern as shown in Figure 7.7. As indicated in the figure, an RUC can be identified from the architecture that remains unchanged when the plain weave reinforcement is infiltrated with a polymer matrix to form a composite. The triply periodic GMC RUC representation of the plain weave composite is shown in Figure 7.8, with an exploded view given in Figure 7.9. As shown, the subcells within the triply periodic RUC are themselves occupied by composite materials that represent the fiber tows of the weave. In addition, some subcells are occupied by the pure matrix material. Figure 7.9 clearly shows the three-dimensional nature of the woven reinforcement as the fiber tows undulate in and out of each other.

In this example problem, the composite material within subcells is represented using the transversely isotropic elastic model with arbitrary plane of isotropy (CMOD = 9). The ability to employ the arbitrary direction of transverse isotropy allows the representation of the subcells containing inclined fibers in Figure 7.9. The material system considered is graphite/epoxy. The effective properties of the composite subcells have been taken from Example 1a (see Table 1.1), which determined the effective properties of a 0.65 fiber volume fraction unidirectional graphite/epoxy composite. Thus, in the present example problem, it is assumed that the infiltrated fiber tows that occupy the subcells have a fiber volume fraction of 0.65. Due to the chosen dimension (a, g, and H in Figure 7.8) this results in an overall woven composite fiber volume fraction of 0.325.

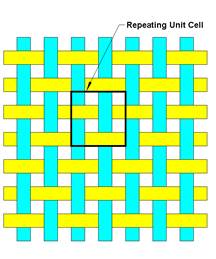
Figure 7.7 Top view of the plain weave architecture with the repeating unit cell identified.

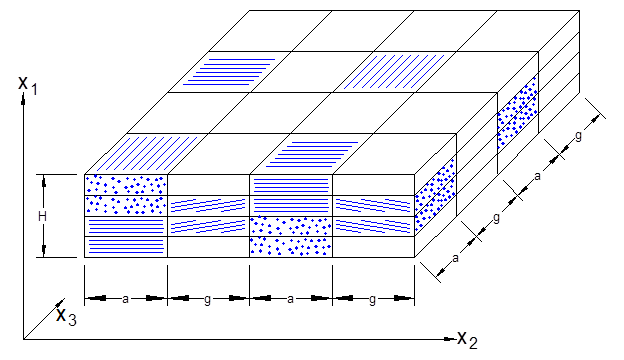
Figure 7.8 MAC/GMC 4.0 triply periodic RUC that represents a plain weave reinforced composite.

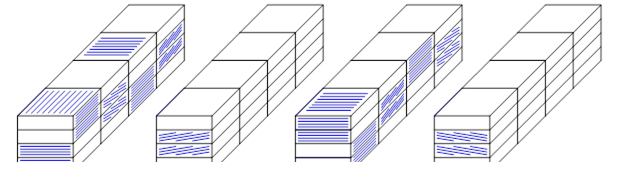
Figure 7.9 MAC/GMC 4.0 triply periodic RUC that represents a plain weave reinforced composite – exploded view.

MAC/GMC Input File: example_7d.mac

MAC/GMC 4.0 Example 7d - graphite/epoxy plain weave reinforced composite

*CONSTITUENTS

NMATS=7

M=1 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.,0.,1.

M=2 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.,1.,0.

M=3 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.25,1.,0.

M=4 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=-0.25,1.,0.

M=5 CMOD=6 MATID=U MATDB=1 &

EL=3.45E9,3.45E9,0.35,0.35,1.278E9,45.E-6,45.E-6

M=6 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.25,0.,1.

M=7 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=-0.25,0.,1.

*RUC

MOD=3 ARCHID=99

NA=4 NB=4 NG=4

D=0.25,0.25,0.25,0.25

H=1.,1.,1.,1.

L=1.,1.,1.,1.

# -- gamma = 1

SM=1,5,2,5

SM=1,3,2,4

SM=2,3,1,4

SM=2,5,1,5

# -- gamma = 2

SM=5,5,5,5

SM=7,5,6,5

SM=5,5,5,5

# -- gamma = 3

SM=2,5,1,5

SM=2,4,1,3

SM=1,4,2,3

SM=1,5,2,5

# -- gamma = 4

SM=5,5,5,5

SM=6,5,7,5

SM=5,5,5,5

*PRINT

NPL=-1

*END

Annotated Input Data

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 7 (NMATS=7)

Constitutive models: Arbitrary transversely isotropic (CMOD=9)

Elastic (CMOD=6)

Materials: User-defined (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 1.1 (EL=…)

Direction of trans. Isotropy: Material #1: (0, 0, 1) (D=0.,0.,1.)

Material #2: (0, 1, 0) (D=0.,1.,0.)

Material #3: (0.25, 1, 0) (D=0.25,1.,0.)

Material #4: (-0.25, 1, 0) (D=-0.25,1.,0.)

Material #6: (0.25, 0, 1) (D=0.25,0.,1.)

Material #7: (-0.25, 0, 1) (D=-0.25,0.,1.)

Table 7.1 Constituent material properties for example 7d.

E_A

(GPa)

E_T

(GPa)

n_A

n_T

G_A

(GPa)

a_A

(10^-6/ °C)

a_T

(10^-6/ °C)

Composite

253.5

6.05

0.3901

0.4682

4.167

-0.4724

6.63

Epoxy

3.45

0.35

1.278

45.

In this example problem, the material occupying many of the subcells represents a unidirectional composite material (see Figure 7.8 and Figure 7.9) intended to model the infiltrated graphite/epoxy fiber tow of which the woven composite reinforcement is composed. Thus, transversely isotropic effective properties for the unidirectional composite material, taken from the results of Example 1a, are specified (for materials #1 – 4 and 6 – 7). Material #5 is the pure isotropic epoxy matrix material. In order to account for the directionality of the fibers in each subcell, the direction vector (D=) is used to specify the direction of transverse isotropy for each of the six transversely isotropic constituent materials. As indicated, a slope of ¼ (D=0.25,…) has been employed for the inclined fibers in the appropriate subcells. When placed in the correct arrangement (under *RUC), these constituent materials will represent the plain weave reinforced composite shown in Figure 7.8. For more information on constitutive material properties, see the MAC/GMC 4.0 Keywords Manual Section 2.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Triply periodic GMC (MOD=3)

RUC architecture: User-defined (ARCHID=99)

No. subcells in x1-dir.: 4 (NA=4)

No. subcells in x2-dir.: 4 (NB=4)

No. subcells in x3-dir.: 4 (NG=4)

Subcell depths: 0.25, 0.25, 0.25, 0.25 (D=0.25,0.25,0.25,0.25)

Subcell heights: 1., 1., 1., 1. (H=1.,1.,1.,1.)

Subcell lengths: 1., 1., 1., 1. (L=1.,1.,1.,1.)

Material assignment: see input file (SM=…)

4) Loading: None

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: -1 (effective properties only) (NPL=-1)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

The results from this example problem are the predicted effective properties of the woven composite printed to the MAC/GMC 4.0 output file:

CG - Effective/Macro Stiffness Matrix

NOTE: Stiffness relates stresses to normal and ENGINEERING SHEAR STRAINS

0.6650E+10 0.3432E+10 0.3432E+10 0.0000E+00 0.3260E-08 0.0000E+00

0.3432E+10 0.1061E+11 0.2873E+10 0.0000E+00 -0.1010E-26 -0.9413E-08

0.3432E+10 0.2873E+10 0.1061E+11 0.0000E+00 -0.4891E-09 -0.9458E-09

0.0000E+00 0.0000E+00 0.0000E+00 0.2079E+10 0.0000E+00 0.0000E+00

0.1281E-08 0.1164E-09 -0.3193E-09 0.0000E+00 0.1859E+10 0.0000E+00

-0.4657E-09 -0.1791E-09 -0.1979E-08 0.0000E+00 0.5404E-28 0.1859E+10

Effective Engineering Moduli

Use with caution when global stiffness matrix is anisotropic

E11S= 0.4902E+10

N12S= 0.2545

E22S= 0.8703E+10

N23S= 0.1245

E33S= 0.8703E+10

G23S= 0.2079E+10

G13S= 0.1859E+10

G12S= 0.1859E+10

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.4267E-04 0.2045E-04 0.2045E-04

0.0000E+00 -0.2846E-22 0.3251E-22

The effective stiffness matrix results show that, even through materials #3, #4, #6, and #7 are monoclinic (in the global coordinates of the woven composite), the woven composite is orthotropic. This is because for every subcell that contains inclined fibers, there is a subcell containing fibers with the incline reversed (see Figure 7.9). The anisotropic terms thus add to zero during the GMC triply periodic homogenization procedure. The same is true of the “shear” CTE terms.

For a woven composite such as the plain weave graphite/epoxy modeled here, the in-plane properties (i.e., x₂-x₃ plane) properties are the most important. This is because woven composites are often made in thin plate form. Thus, the in-plane properties for the woven composite predicted by this single step GMC homogenization procedure are:

E = 8.703 GPa, n = 0.1245, G = 2.079 GPa, and a = 20.45´10^-6 /°C

Thus, these predictions indicate that the in-plane elastic modulus of 8.703 GPa is quite small, on the order of the transverse elastic modulus of the fiber (7.6 GPa) and the elastic modulus of the epoxy (3.45 GPa). The extreme longitudinal stiffness of the fiber (388.2 GPa) appears not to impart much stiffness to the woven composite in this single step homogenization procedure. For an alternative two step procedure, which has been shown to be significantly more accurate (particularly in the case of large constituent property mismatch), see Example 7e.

Example 7e: Woven Composite Analysis – Two Step

This example considers the previous plain weave graphite/epoxy composite considered in Example 7d. In this example, however, a two step approach is employed to homogenize the triply periodic RUC in order to arrive at the effective properties of the composite. This two step homogenization procedure has been shown to yield significantly more accurate effective properties for the composite than the one step approach demonstrated in Example 7d (Bednarcyk, 2000).

Considering the plain weave reinforced composite shown in Figure 7.8, the six unique through-thickness subcell groups shown in Figure 7.10 can be identified. Note that reversing the stacking sequence of Group 1 does not result in a unique through-thickness subcell group. In step one of the two step homogenization procedure, the six unique subcell groups are individually homogenized in the through-thickness direction. The result is a set of effective thermo-elastic properties for each of the groups. Note that, since Group 5 consists only of matrix material, its effective properties are that of the matrix. Further, Groups 2, 3, 4, and 6 contain subcells with inclined fibers. Thus, the effective properties of these Groups will be monoclinic.

Once the effective properties of each through-thickness subcell group are determined, an RUC, with only one through-thickness subcell, can be assembled that represents the woven composite. This is shown in Figure 7.11, where the effective properties of the appropriate through-thickness group are used to represent the subcell materials. Then, as step two of the procedure, this two-dimensional RUC is homogenized to determine the effective properties of the woven composites. As will be shown, the results of this two step homogenization procedure can be quite different from those of the corresponding one step homogenization procedure.

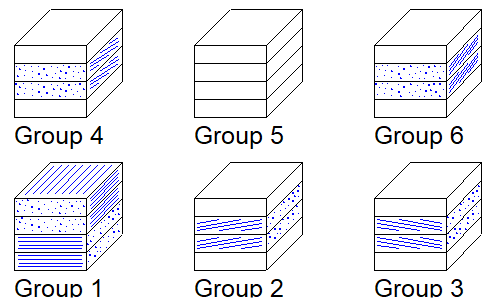
Figure 7.10 Unique through-thickness groups in the plain weave reinforced composite shown in Figure 7.8. These through-thickness subcell groups are homogenized using MAC/GMC 4.0 to determine their effective stiffness matrices in Step 1 of the two step homogenization procedure.

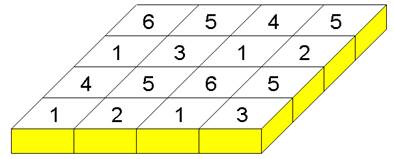
Figure 7.11 Representation of the plain-weave reinforced composite after though-thickness homogenization in Step 1. Step 2 involves homogenizing this RUC to determine the effective properties of the plain weave reinforced composite.

MAC/GMC Input Files: example_7e_1.mac, example_7e_2.mac

MAC/GMC 4.0 Example 7e_1 - Two step plain weave composite analysis (step 1)

*CONSTITUENTS

NMATS=7

M=1 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.,0.,1.

M=2 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.,1.,0.

M=3 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.25,1.,0.

M=4 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=-0.25,1.,0.

M=5 CMOD=6 MATID=U MATDB=1 &

EL=3.45E9,3.45E9,0.35,0.35,1.278E9,45.E-6,45.E-6

M=6 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=0.25,0.,1.

M=7 CMOD=9 MATID=U MATDB=1 &

EL=253.5E9,6.05E9,0.3901,0.4682,4.167E9,-0.4724E-6,26.63E-6 D=-0.25,0.,1.

*RUC

MOD=3 ARCHID=99

NA=4 NB=1 NG=1

D=0.25,0.25,0.25,0.25

H=1.

L=1.

# -- Group 1

SM=1

SM=2

# -- Group 2

# SM=5

# SM=3

# SM=5

# -- Group 3

# SM=5

# SM=4

# SM=5

# -- Group 4

# SM=5

# SM=7

# SM=5

# -- Group 6

# SM=5

# SM=6

# SM=5

*PRINT

NPL=-1

*END

MAC/GMC 4.0 Example 7e_2 - Two step plain weave composite analysis (step 2)

*CONSTITUENTS

NMATS=6

M=1 CMOD=15 MATID=U MATDB=1 &

EL=7.827E9, 4.103E9, 4.103E9, 0., 0., 0., &

132.4E9, 4.519E9, 0., 0., 0., &

132.4E9, 0., 0., 0., &

4.167E9, 0., 0., &

2.757E9, 0., &

2.757E9 &

38.56E-6, 0.3901E-6, 0.3901E-6, 0., 0., 0.

M=2 CMOD=15 MATID=U MATDB=1 &

EL=6.677E9, 4.843E9, 3.274E9, 0., 0., 0.1887E9, &

55.80E9, 3.384E9, 0., 0., 6.969E9, &

6.662E9, 0., 0., -0.006711E9, &

2.625E9, 0.1830E9, 0., &

1.613E9, 0., &

2.269E9 &

43.74E-6, 4.043E-6, 39.04E-6, 0., 0., -12.19E-6

M=3 CMOD=15 MATID=U MATDB=1 &

EL=6.677E9, 4.843E9, 3.274E9, 0., 0., -0.1887E9, &

55.80E9, 3.384E9, 0., 0., -6.969E9, &

6.662E9, 0., 0., 0.006711E9, &

2.625E9,-0.1830E9, 0., &

1.613E9, 0., &

2.269E9 &

43.74E-6, 4.043E-6, 39.04E-6, 0., 0., 12.19E-6

M=4 CMOD=15 MATID=U MATDB=1 &

EL=6.677E9, 3.274E9, 4.843E9, 0., -0.1887E9, 0., &

6.662E9, 3.384E9, 0., 0.006711E9, 0., &

55.80E9, 0., -6.969E9, 0., &

2.625E9, 0., -0.1830E9, &

2.269E9, 0., &

1.613E9 &

43.74E-6, 39.04E-6, 4.043E-6, 0., 12.19E-6, 0.

M=5 CMOD=6 MATID=U MATDB=1 &

EL=3.45E9,3.45E9,0.35,0.35,1.278E9,45.E-6,45.E-6

M=6 CMOD=15 MATID=U MATDB=1

NTP=2

TEM=23.,150.

C11=6.677E9,6.677E9

C12=3.274E9,3.274E9

C13=4.843E9,4.843E9

C14=0.,0.

C15=0.1887E9,0.1887E9

C16=0.,0.

C22=6.662E9,6.662E9

C23=3.384E9,3.384E9

C24=0.,0.

C25=-0.006711E9,-0.006711E9

C26=0.,0.

C33=55.80E9,55.80E9

C34=0.,0.

C35=6.969E9,6.969E9

C36=0.,0.

C44=2.625E9,2.625E9

C45=0.,0.

C46=0.1830E9,0.1830E9

C55=2.269E9,2.269E9

C56=0.,0.

C66=1.613E9,1.613E9

ALF1=43.74E-6,43.74E-6

ALF2=39.04E-6,39.04E-6

ALF3=4.043E-6,4.043E-6

ALF4=0.,0.

ALF5=-12.19E-6,-12.19E-6

ALF6=0.,0.

*RUC

MOD=3 ARCHID=99

NA=1 NB=4 NG=4

D=1.

H=1.,1.,1.,1.

L=1.,1.,1.,1.

SM=1,2,1,3

SM=4,5,6,5

SM=1,3,1,2

SM=6,5,4,5

*PRINT

NPL=-1

*END

Annotated Input Data

Step 1: Homogenization of the through-thickness subcell groups ® example_7e_1.mac

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 7 (NMATS=7)

Constitutive models: Arbitrary transversely isotropic (CMOD=9)

Elastic (CMOD=6)

Materials: User-defined (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See Table 1.1 (EL=…)

Direction of trans. Isotropy: Material #1: (0, 0, 1) (D=0.,0.,1.)

Material #2: (0, 1, 0) (D=0.,1.,0.)

Material #3: (0.25, 1, 0) (D=0.25,1.,0.)

Material #4: (-0.25, 1, 0) (D=-0.25,1.,0.)

Material #6: (0.25, 0, 1) (D=0.25,0.,1.)

Material #7: (-0.25, 0, 1) (D=-0.25,0.,1.)

In this example problem, the constituent materials are the same as those employed in Example 7d.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Triply periodic GMC (MOD=3)

RUC architecture: User-defined (ARCHID=99)

No. subcells in x1-dir.: 4 (NA=4)

No. subcells in x2-dir.: 1 (NB=1)

No. subcells in x3-dir.: 1 (NG=1)

Subcell depths: 0.25, 0.25, 0.25, 0.25 (D=0.25,0.25,0.25,0.25)

Subcell height: 1. (H=1.)

Subcell length: 1. (L=1.)

Material assignment: see input file (SM=…)

In this example problem, effective elastic properties must be generated for each of five subcell groups. Recall that Group 5 contains only the matrix material and thus does not need to be homogenized. The appropriate lines in the input file must be commented and uncommented in order to generate all of these effective properties.

4) Loading: None

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: -1 (effective properties only) (NPL=-1)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Step 2: Homogenization of the 2D RUC ® example_7e_2.mac

1) Flags: None

2) Constituent materials (*CONSTITUENTS) [KM_2]:

Number of materials: 6 (NMATS=6)

Constitutive models: Anisotropic elastic (CMOD=15)

Elastic (CMOD=6)

Materials: User-defined (MATID=U)

Material property source: Read from input file (MATDB=1)

Material properties: See input file (EL=…)

In step two of this example problem, the material occupying many of the subcells represents homogenized subcell groups that contain subcells with inclined fibers (see Figure 7.10). These materials are monoclinic and thus require a more general elastic constitutive model than presented this far in this Example Manual. For this reason, a completely anisotropic elastic model (CMOD=15) has been incorporated within MAC/GMC 4.0. This model allows the user to specify all 21 components of the constituent material stiffness matrix, as well as six CTE components. For material #6, the use of this model in conjunction with temperature-dependent material properties is illustrated. For more information on constituent materials, see the MAC/GMC 4.0 Keywords Manual Section 2.

3) Analysis type (*RUC) ® Repeating Unit Cell Analysis [KM_3]:

Analysis model: Triply periodic GMC (MOD=3)

RUC architecture: User-defined (ARCHID=99)

No. subcells in x1-dir.: 1 (NA=1)

No. subcells in x2-dir.: 4 (NB=4)

No. subcells in x3-dir.: 4 (NG=4)

Subcell depth: 1. (D=1.)

Subcell heights: 1., 1., 1., 1. (H=1.,1.,1.,1.)

Subcell lengths: 1., 1., 1., 1. (L=1.,1.,1.,1.)

Material assignment: see input file (SM=…)

The anisotropic materials that represent the homogenized subcell groups are arranged as shown in Figure 7.11 to represent the plain weave reinforced composite. Note that the anisotropic constitutive model can only be used with triply-periodic GMC (i.e., the doubly periodic GMC implementation assumes the subcell materials to be at most orthotropic in the RUC coordinate system). Thus, even though the RUC in this example problem is two-dimensional, triply periodic GMC (with one x₁-direction subcell) has been employed. For more information on the MAC/GMC 4.0 RUC capabilities, see the MAC/GMC 4.0 Keywords Manual Section 3.

4) Loading: None

5) Damage and Failure: None

6) Output:

a) Output file print level (*PRINT) [KM_6]:

Print level: -1 (effective properties only) (NPL=-1)

b) x-y plots (*XYPLOT): None

7) End of file keyword: (*END)

Results

Results for this example problem take the form of the effective thermo-elastic properties of the subcell groups (in step 1) and of the plain weave reinforced graphite/epoxy composite (step 2). The effective stiffness matrix, elastic moduli, and CTEs of each through-thickness subcell group (determined in step 1) are given below. Because Group 1 contains no subcells with inclined fibers, the group’s effective thermo-elastic properties are orthotropic. The remaining subcell groups (with the exception of Group 5, which contains only the matrix material and thus does not need to be homogenized in step 1) do contain subcells with inclined fibers. The effective elastic behavior of these homogenized subcell groups is monoclinic (i.e., 13 independent constants, see Jones (1975)). The non-zero C₁₆ term for Group 2 indicates that, for example, a non-zero shear stress s₁₂ component would arise were a normal strain component e₁₁ applied. In addition, each monoclinic subcell group has a non-zero shear CTE. This indicates that, were a temperature change applied to the subcell group, a shear strain component would arise. The effective stiffness matrix of each group, as well as the effective CTEs, are employed as constituent material properties in step 2 of the homogenization procedure.

GROUP 1

CG - Effective/Macro Stiffness Matrix

NOTE: Stiffness relates stresses to normal and ENGINEERING SHEAR STRAINS

0.7827E+10 0.4103E+10 0.4103E+10 0.0000E+00 0.0000E+00 0.0000E+00

0.4103E+10 0.1324E+12 0.4519E+10 0.0000E+00 0.0000E+00 0.0000E+00

0.4103E+10 0.4519E+10 0.1324E+12 0.0000E+00 0.0000E+00 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.4167E+10 0.0000E+00 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.2757E+10 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.0000E+00 0.2757E+10

Effective Engineering Moduli

Use with caution when global stiffness matrix is anisotropic

E11S= 0.7581E+10

N12S= 0.0300

E22S= 0.1302E+12

N23S= 0.0182

E33S= 0.1302E+12

G23S= 0.4167E+10

G13S= 0.2757E+10

G12S= 0.2757E+10

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.3856E-04 0.3901E-06 0.3901E-06

0.0000E+00 0.0000E+00 0.0000E+00

GROUP 2

CG - Effective/Macro Stiffness Matrix

NOTE: Stiffness relates stresses to normal and ENGINEERING SHEAR STRAINS

0.6677E+10 0.4843E+10 0.3274E+10 0.0000E+00 0.0000E+00 0.1887E+09

0.4843E+10 0.5580E+11 0.3384E+10 0.0000E+00 0.0000E+00 0.6969E+10

0.3274E+10 0.3384E+10 0.6662E+10 0.0000E+00 0.0000E+00 -0.6711E+07

0.0000E+00 0.0000E+00 0.0000E+00 0.2625E+10 0.1830E+09 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.1830E+09 0.1613E+10 0.0000E+00

0.3775E+09 0.5575E+10 -0.5369E+07 0.0000E+00 0.0000E+00 0.2269E+10

Effective Engineering Moduli

Use with caution when global stiffness matrix is anisotropic

E11S= 0.4889E+10

N12S= 0.0733

E22S= 0.3586E+11

N23S= 0.3140

E33S= 0.4994E+10

G23S= 0.2604E+10

G13S= 0.1600E+10

G12S= 0.1552E+10

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.4374E-04 0.4043E-05 0.3904E-04

0.0000E+00 0.0000E+00 -0.1219E-04

GROUP 3

CG - Effective/Macro Stiffness Matrix

NOTE: Stiffness relates stresses to normal and ENGINEERING SHEAR STRAINS

0.6677E+10 0.4843E+10 0.3274E+10 0.0000E+00 0.0000E+00 -0.1887E+09

0.4843E+10 0.5580E+11 0.3384E+10 0.0000E+00 0.0000E+00 -0.6969E+10

0.3274E+10 0.3384E+10 0.6662E+10 0.0000E+00 0.0000E+00 0.6711E+07

0.0000E+00 0.0000E+00 0.0000E+00 0.2625E+10 -0.1830E+09 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 -0.1830E+09 0.1613E+10 0.0000E+00

-0.3775E+09 -0.5575E+10 0.5369E+07 0.0000E+00 0.0000E+00 0.2269E+10

Effective Engineering Moduli

Use with caution when global stiffness matrix is anisotropic

E11S= 0.4889E+10

N12S= 0.0733

E22S= 0.3586E+11

N23S= 0.3140

E33S= 0.4994E+10

G23S= 0.2604E+10

G13S= 0.1600E+10

G12S= 0.1552E+10

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.4374E-04 0.4043E-05 0.3904E-04

0.0000E+00 0.0000E+00 0.1219E-04

GROUP 4

CG - Effective/Macro Stiffness Matrix

NOTE: Stiffness relates stresses to normal and ENGINEERING SHEAR STRAINS

0.6677E+10 0.3274E+10 0.4843E+10 0.0000E+00 -0.1887E+09 0.0000E+00

0.3274E+10 0.6662E+10 0.3384E+10 0.0000E+00 0.6711E+07 0.0000E+00

0.4843E+10 0.3384E+10 0.5580E+11 0.0000E+00 -0.6969E+10 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.2625E+10 0.0000E+00 -0.1830E+09

-0.3775E+09 0.5369E+07 -0.5575E+10 0.0000E+00 0.2269E+10 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 -0.1830E+09 0.0000E+00 0.1613E+10

Effective Engineering Moduli

Use with caution when global stiffness matrix is anisotropic

E11S= 0.4889E+10

N12S= 0.4541

E22S= 0.4994E+10

N23S= 0.0343

E33S= 0.3586E+11

G23S= 0.2604E+10

G13S= 0.1552E+10

G12S= 0.1600E+10

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.4374E-04 0.3904E-04 0.4043E-05

0.0000E+00 0.1219E-04 0.0000E+00

GROUP 6

CG - Effective/Macro Stiffness Matrix

NOTE: Stiffness relates stresses to normal and ENGINEERING SHEAR STRAINS

0.6677E+10 0.3274E+10 0.4843E+10 0.0000E+00 0.1887E+09 0.0000E+00

0.3274E+10 0.6662E+10 0.3384E+10 0.0000E+00 -0.6711E+07 0.0000E+00

0.4843E+10 0.3384E+10 0.5580E+11 0.0000E+00 0.6969E+10 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.2625E+10 0.0000E+00 0.1830E+09

0.3775E+09 -0.5369E+07 0.5575E+10 0.0000E+00 0.2269E+10 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.1830E+09 0.0000E+00 0.1613E+10

Effective Engineering Moduli

Use with caution when global stiffness matrix is anisotropic

E11S= 0.4889E+10

N12S= 0.4541

E22S= 0.4994E+10

N23S= 0.0343

E33S= 0.3586E+11

G23S= 0.2604E+10

G13S= 0.1552E+10

G12S= 0.1600E+10

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.4374E-04 0.3904E-04 0.4043E-05

0.0000E+00 -0.1219E-04 0.0000E+00

STEP 2 RESULTS (Effective Properties of the Woven Composite)

The results of step 2 in the two step homogenization procedure for the plain weave reinforced graphite/epoxy composite are the predicted effective thermo-elastic properties of the woven composite. As in Example 7d, the effective stiffness matrix results show that, even through Groups 2, 3, 4, and 6 are monoclinic (in the global coordinates of the woven composite), the woven composite is orthotropic. This is because for every subcell that contains inclined fibers, there is a subcell containing fibers with the incline reversed (see Figure 7.9). The anisotropic terms thus add to zero during the GMC triply periodic homogenization procedure. The same is true of the “shear” CTE terms.

Table 7.2 provides a comparison of the MAC/GMC 4.0 prediction for the in-plane (i.e., plane of the woven reinforcement) thermo-elastic properties of the woven composite. The effect of utilizing the 2 step approach rather than the 1 step approach is stunning. The predicted in plane elastic modulus is 3.2 times higher, the predicted in-plane Poisson ratio is 2.3 times lower, and the predicted in-plane CTE is 2.9 times lower. The effect on the predicted in-plane shear modulus is less significant; it is only 7.5% higher when using the 2 step approach. The reason for this dramatic effect on the effective properties is the fact that the triply periodic RUC that represents the woven composite (see Figure 7.8 and Figure 7.9) has no continuous fibers spanning the x₂- and x₃-directions. Following any row or column of subcells in the x₂- and x₃-directions (at a constant x₁ position), a subcell containing either the pure matrix material or transversely oriented fibers will be encountered. These subcells serve as weak links and cause the 1 step homogenization approach to predict a low effective in-plane stiffness (along with a high in-plane Poisson ratio and CTE). In the 2 step homogenization procedure, the woven composite properties are homogenized, or “smeared”, in the through-thickness (x₁) direction in step 1. This, in effect, removes the extreme weak links from the RUC. In Figure 7.11, two rows of subcells in the x₂-direction exists that contain only homogenized Groups 1, 2, and 3, while in the x₃-direction, two columns of subcells exist that contain only homogenized Groups 1, 4, and 6 (the remaining two rows or columns in the two directions do contain extreme weak link subcells). Examining Figure 7.10, it is clear that, while Groups 2, 3, 4, and 6 are less stiff than Group 1, they still contain subcells with fibers mainly aligned in the appropriate in-plane direction. This fact can also be seen in the effective properties of the Groups given above. Therefore, the RUC depicted in Figure 7.11 has two rows or columns of subcells in each of the in-plane directions that do not contain extreme weak link subcells. The result is the stiffer predicted composite properties obtained in the 2 step approach. Note that the large constituent property mismatch between the graphite fiber and epoxy matrix in the present example magnifies the discrepancy between the 1 step and 2 step approaches. A significant improvement in the 1 step procedure will result from the use of HFGMC rather than GMC to model the woven composite. However, in order to model the architecture of the woven reinforcement, triply periodic HFGMC is required. This theory is currently under development.

Finally, Bednarcyk (2000) showed that the 2 step MAC/GMC homogenization procedure provides much more accurate predictions of woven composite properties than does the 1 step approach. The two step approach is somewhat cumbersome compared to most of the other features within MAC/GMC 4.0. Future versions of MAC/GMC will automate the woven composite analysis procedure in order to relieve this burden from the user.

CG - Effective/Macro Stiffness Matrix

NOTE: Stiffness relates stresses to normal and ENGINEERING SHEAR STRAINS

0.6669E+10 0.3662E+10 0.3662E+10 0.0000E+00 0.5215E-07 0.2980E-07

0.3662E+10 0.3022E+11 0.3562E+10 0.0000E+00 0.2068E-24 0.0000E+00

0.3662E+10 0.3562E+10 0.3022E+11 0.0000E+00 0.5679E-08 0.0000E+00

0.0000E+00 0.0000E+00 0.0000E+00 0.2234E+10 0.0000E+00 0.0000E+00

-0.4657E-08 0.0000E+00 0.3950E-09 0.0000E+00 0.1626E+10 0.0000E+00

-0.1397E-08 0.4740E-08 0.3725E-08 0.0000E+00 0.0000E+00 0.1626E+10

Effective Engineering Moduli

Use with caution when global stiffness matrix is anisotropic

E11S= 0.5875E+10

N12S= 0.1084

E22S= 0.2813E+11

N23S= 0.0550

E33S= 0.2813E+11

G23S= 0.2234E+10

G13S= 0.1626E+10

G12S= 0.1626E+10

Effective Thermal Expansion Coefficients

NOTE: Shear CTEs are "engineering" shear CTEs

0.5595E-04 0.7048E-05 0.7048E-05

0.0000E+00 -0.1206E-21 0.1138E-22

Table 7.2 Predicted effective in-plane thermo-elastic properties for 32.5% plain weave reinforced graphite/epoxy composite using the MAC/GMC 4.0 1 step and 2 step homogenization procedures.

	E (GPa)	n	G (GPa)	a (´10^-6 /°C)
1 Step Approach	8.703	0.1245	2.079	20.45
2 Step Approach	28.13	0.0550	2.234	7.048

References

Aboudi, J. (1987) “Damage in Composites – Modeling of Imperfect Interfaces” Composites Science and Technology 28, 103-128.

Achenbach, J.D. and Zhu, H. (1989) “Effect of Interfacial Zone on Mechanical Behavior and Failure of Fiber-Reinforced Composites” Journal of the Mechanics and Physics of Solids 37(3), 381-393.

Arnold, S.M. and Kruch, S. (1994) “Differential Continuum Damage Mechanics Models for Creep and Fatigue of Unidirectional Metal Matrix Composites” International Journal of Damage Mechanics 3(2), 170-191.

Bednarcyk, B.A. (2000) “Modeling Woven Polymer Matrix Composites With MAC/GMC” NASA/CR–2000-210370.

Bednarcyk, B.A. and Arnold, S.M. (2001) “Micromechanics-Based Deformation and Failure Prediction for Longitudinally Reinforced Titanium Composites” Composites Science and Technology 61, 705-729.

Bednarcyk, B.A. and Arnold, S.M. (2002) “Transverse Tensile and Creep Modeling of Continuously Reinforced Titanium Composites with Local Debonding” International Journal of Solids and Structures 39, 1987-2017.

Curtin, W.A. (1991) “Theory of Mechanical Properties of Ceramic-Matrix Composites” Journal of the American Ceramics Society 74(11), 2837-2845.

Curtin, W.A. (1993) “Ultimate Strengths of Fibre-Reinforced Ceramics and Metals” Composites 24(2), 98-102.

Goldberg, R.K., Comiskey, M.D., and Bednarcyk, B.A. (1999) “Micromechanics Analysis Code Post-Processing (MACPOST) User Guide Version 1.0” NASA/TM–1999-209062.

Jones, J.P. and Whittier, J.S. (1967) “Waves at Flexibly Bonded Interfaces” Journal of Applied Mechanics 34, 905-909.

Jones, R.M. (1974) “Stiffness of Orthotropic Materials and Laminated Fiber-Reinforced Composites” AIAA Journal, January, pp. 112-114.

Jones, R.M. (1975) Mechanics of Composite Materials, Hemisphere Publishing Corp., New York.

Pahr, D.H. and Arnold, S.M. (2002) “The Applicability of the Generalized Method of Cells for Analyzing Discontinuously Reinforced Composites” Composites: Part B 33, 153-170.

Paley, M. and Aboudi, J. (1992) “Micromechanical Analysis of Composites by the Generalized Cells Model” Mechanics of Materials 14, 127-139.

Plastics Design Library (1995) Fatigue and Tribological Properties of Plastics and Elastomers. Plastics Design Library, William Andrew, Inc., Norwich, NY.

Saleeb, A.F., Arnold, S.M., Castelli, M.G., Wilt, T.E., and Graf, W. (2001) “A General Hereditary Multimechanism-Based Deformation Model with Application to the Viscoelastoplastic Response of Titanium Alloys” International Journal of Plasticity 17, 1305-1350.

Wilt, T.E. and Arnold, S.M. (1996) “Micromechanics Analysis Code (MAC) User Guide: Version 2.0” NASA-TM-107290.

Wilt, T.E., Arnold, S.M., and Saleeb, A.F. (1997) “A Coupled/Uncoupled Computational Scheme for Deformation and Fatigue Damage Analysis of Unidirectional Metal Matrix Composites” in Applications of Continuum Damage Mechanics to Fatigue and Fracture, D.L. McDowell (ed.), ASTM STP 1315, American Society for Testing and Materials, 65-82.

Appendix

This Appendix contains the following:

· Complete MAC/GMC 4.0 output file for Example Problem 4.0

· Complete distribution (default) version of the usrfun.F90 subroutine

· Complete distribution (default) version of the usrmat.F90 subroutine

· Complete distribution (default) version of the usrformde.F90 subroutine

Complete output file for Example 1a

__ __ ____ _______

/ |/ | / | / _____/

/ | / /| | / /

/ /|_/| | / /_| | / /

/ / | | / ___ | / /_____

/_/ |_|icromechanics /_/ |_|nalysis \______/ode

with

_______ __ __ _______

/ _____/ / |/ | / _____/

/ / ____ / | / /

/ / /_ / / /|_/| | / /

/ /___/ / / / | | / /_____

\______/eneralized /_/ |_|ethod of \______/ells

Version 4.0

NASA Glenn Research Center

Ohio Aerospace Institute

Point of Contact:

Dr. Steven M. Arnold

NASA Glenn Research Center

http://www.grc.nasa.gov/WWW/LPB/mac/index.html

___________________________________________________________________________

Disclaimer: This software package is considered to be a research code

and therefore no expressed or implied warranties are granted

pertaining to the results produced from the use of this code

___________________________________________________________________________

*** WARNING *** This code is export controlled - unauthorized transmission

to non-U.S. citizens may be a violation of federal law

___________________________________________________________________________

================================================================================================

Execution Initiated ---> 15:38:50 11-22-2002

================================================================================================

Input file ---> C:\mac\mac119\example_1a.mac

Output file --> C:\mac\mac119\test.out

******* PROBLEM TITLE ** PROBLEM TITLE ** PROBLEM TITLE ** PROBLEM TITLE ** PROBLEM TITLE *******

MAC/GMC 4.0 Example 1a - graphite/epoxy effective properties

*************************************************************************************************

================================================================================================

***** Section I: Problem Input Data *****

================================================================================================

------------------------------------------------------------------------------------------------

** A: Execution Flags **

------------------------------------------------------------------------------------------------

Thermal Conductivities Requested

At the following temperatures:

0.2100E+02

No Electro-Magnetic Properties Requested

------------------------------------------------------------------------------------------------

** B: Constituent Material Information **

------------------------------------------------------------------------------------------------

Database material data (if selected) will be read from *internal* database

Number of constituent materials (nmats) = 2

COMMENT: # -- GRAPHITE FIBER

---------------------------------------------------------

MATERIAL # 1

---------------------------------------------------------

Constitutive Model Chosen:

Standard Elastic Model (RUC X2-X3 Plane of Transverse Isotropy)

(CH1) = U

User input material properties

Material properties read from input file

Thermal Conductivities:

Axial = 0.500E+03

Transverse = 0.100E+02

Elastic Properties:

1) E Longitudinal = 0.3882D+12

2) E Transverse = 0.7600D+10

3) Nu Longitudinal = 0.4100D+00

4) Nu Transverse = 0.4500D+00

5) G = 0.1490D+11

6) Alpha Longitudinal = -.6800D-06

7) Alpha Transverse = 0.9740D-05

COMMENT: # -- EPOXY MATRIX

---------------------------------------------------------

MATERIAL # 2

---------------------------------------------------------

Constitutive Model Chosen:

Standard Elastic Model (RUC X2-X3 Plane of Transverse Isotropy)

(CH1) = U

User input material properties

Material properties read from input file

Thermal Conductivities:

Axial = 0.190E+00

Transverse = 0.190E+00

Elastic Properties:

1) E Longitudinal = 0.3450D+10

2) E Transverse = 0.3450D+10

3) Nu Longitudinal = 0.3500D+00

4) Nu Transverse = 0.3500D+00

5) G = 0.1278D+10

6) Alpha Longitudinal = 0.4500D-04

7) Alpha Transverse = 0.4500D-04

------------------------------------------------------------------------------------------------

** C: Analysis Type & Architecture Information **

------------------------------------------------------------------------------------------------

--------------------------------------------------

ANALYSIS APPROACH INFORMATION

--------------------------------------------------

Selected Analysis Model: 2

1) Monolithic Material Analysis

2) Double Periodic GMC Micromechanics Model

3) Triple Periodic GMC Micromechanics Model

12) Double Periodic HFGMC Micromechanics Model

--------------------------------------------------

RUC INFORMATION

--------------------------------------------------

Selected RVE = 1

Monolithic Layer = 0

Square Pack With 4 Subcells = 1

Triangular pack = 2

Square Diagonal Pack = 3

Cross Shape Fiber = 4

(Square Pack)

---------------------------

Circular Fiber Approximation = 6

(49 Cell)

Circular Fiber Approximation = 7

(196 Cell)

Square Pack = 9

(Two Fibers of Different Size)

Rectangular Pack = 11

26x26 circular x-section fiber = 13

8x8 circular fiber approx. = 20

10x10 circular fiber approx. = 21

User Defined RVE = 99

Interface IS NOT present

Fiber Volume Ratio = 0.650E+00

Fiber Material ID Number: 1

Matrix Material ID Number: 2

Material Arrangement:

2 2

1 2

Subcell Dimensions:

H = 0.8062 0.1938

L = 0.8062 0.1938

------------------------------------------------------------------------------------------------

** D: Applied Loading & Time Integration Information **

------------------------------------------------------------------------------------------------

No Yield Surface Analysis Requested

------------------------------------------------------------------------------------------------

** E: Damage & Failure Information **

------------------------------------------------------------------------------------------------

No Fatigue Damage Analysis Requested

No Elastic Allowable Estimates Requested

No Subcell Failure Analysis Requested

No RUC Failure Analysis Requested

No Debonding Analysis Requested

No Curtin Effective Fiber Breakage Model Analysis Requested

------------------------------------------------------------------------------------------------

** F: Results Output Information **

------------------------------------------------------------------------------------------------

Print Level (nplvl) = -1

No PATRAN Output Requested

No MATLAB Output Requested

================================================================================================

***** Section II: Effective Property Results *****

================================================================================================

------------------- SUBCELL IDENTIFICATION, VOLUME, AND MATERIAL ARRANGEMENT -------------------

(BETA , GAMMA) SUBCELL # SUBCELL MATERIAL SUBCELL VOLUME

1 , 1 1 1 0.650E+00

1 , 2 2 2 0.156E+00

2 , 1 3 2 0.156E+00

2 , 2 4 2 0.375E-01

TOTAL VOLUME = 0.1000E+01

MATERIAL NO.= 1 VOLUME RATIO= 0.6500E+00

MATERIAL NO.= 2 VOLUME RATIO= 0.3500E+00

------------------------------------------------------------------------------------------------

-------------------------------------------------

Effective Thermal Conductivities

At Temperature = 21.0

K11 = 325.0665

K22 = 0.7694

K33 = 0.7694

-------------------------------------------------

--------------------- EFFECTIVE PROPERTIES AT TEMPERATURE = 21.00 ----------------------------

CG - Effective/Macro Stiffness Matrix

0.2571E+12 0.4500E+10 0.4500E+10

0.4500E+10 0.7828E+10 0.3707E+10

0.4500E+10 0.3707E+10 0.7828E+10

0.1916E+10

0.4166E+10

CI - Effective/Macro Compliance Matrix

0.3944E-11 -0.1539E-11 -0.1539E-11

-0.1539E-11 0.1653E-09 -0.7738E-10

-0.1539E-11 -0.7738E-10 0.1653E-09

0.5219E-09

0.2400E-09

Effective Engineering Moduli

E11S= 0.2535E+12

N12S= 0.3901

E22S= 0.6050E+10

N23S= 0.4682

E33S= 0.6050E+10

G23S= 0.1916E+10

G13S= 0.4166E+10

G12S= 0.4166E+10

Effective Thermal Expansion Coefficients

-0.4724E-06 0.2663E-04 0.2663E-04

------------------------------------------------------------------------------------------------

STOPPING: NPLVL == -1

ENDENDENDENDENDENDENDENDENDENDENDENDENDENDENDEND

_______ ______

/ ____/ | / / __ \\

/ __/ / |/ / / / /

/ /___/ /| / /_/ /

/_____/_/ |_/_____/

ENDENDENDENDENDENDENDENDENDENDENDENDENDENDENDEND

Execution Time: 0.234 second(s)

usrfun.F90: User-defined material property function file

!***********************************************************************

! BEGIN USER EDITS *

!***********************************************************************

! -- Consider placing your own message here to ensure that your code is

! being executed

IF (TIME .EQ. 0.D0) THEN

WRITE(NIO, *) '*** NOTE: Default USRFUN routine being executed ***'

WRITE(NIO, *) ' material number', MN

WRITE(*, *) '*** NOTE: Default USRFUN routine being executed ***'

WRITE(*, *) ' Material number', MN

ENDIF

!-----------------------------------------------------------------------

! MATERIAL # 1: Elastic, E = function of strain & previous E

!-----------------------------------------------------------------------

IF (MN .EQ. 1) THEN

IF (SA(1) .GT. 0) THEN

EAOLD = PEM(1, MN)

EA = 700.E9 - EAOLD * SA(1) * 80.0

ELSE

EA = 700.E9

EAOLD = 700.E9

ENDIF

IF (EA .GT. EAOLD) THEN

WRITE(NIO, *) 'NON-PHYSICAL REGIME ENTERED'

STOP

ENDIF

EA = EA

ET = EA

FNA = 0.41

FNT = 0.41

GA = EA / (2.0 * (1.0 + FNA))

ALPA(MN) = 4.5E-6

ALPT(MN) = 4.5E-6

NE = 5

PEM(1, MN) = EA

PEM(2, MN) = ET

PEM(3, MN) = FNA

PEM(4, MN) = FNT

PEM(5, MN) = GA

EA = EA

ET = EA

FNA = 0.41

FNT = 0.41

GA = EA / (2.0 * (1.0 + FNA))

ALPA(MN) = 4.5E-6

ALPT(MN) = 4.5E-6

NE = 5

PEM(1, MN) = EA

PEM(2, MN) = ET

PEM(3, MN) = FNA

PEM(4, MN) = FNT

PEM(5, MN) = GA

!-----------------------------------------------------------------------

! MATERIAL # 2: Incremental plasticity with strain rate dependence

!-----------------------------------------------------------------------

ELSEIF (MN .EQ. 2) THEN

EA = 13161.

ET = EA

FNA = 0.26

FNT = 0.26

GA = EA / (2.0 * (1.0 + FNA))

ALPA(MN) = 9.00E-6

ALPT(MN) = 9.00E-6

NE = 5

PEM(1, MN) = EA

PEM(2, MN) = ET

PEM(3, MN) = FNA

PEM(4, MN) = FNT

PEM(5, MN) = GA

NP = 3

NV = 2 * NP + 1

STRAIN_RATE = 0.4714 * (DSQRT((DSA(1) - DSA(2))**2 + (DSA(1) - DSA(3))**2 + &

(DSA(2) - DSA(3))**2 + 1.5 * DSA(4)**2 + &

1.5 * DSA(5)**2 + 1.5 * DSA(6)**2)) / TSTEP

IF (STRAIN_RATE .GT. 1.E-2) STRAIN_RATE = 1.E-2

IF (STRAIN_RATE .LT. 1.E-7) THEN

SY = 70.

S1 = 80.

S2 = 84.

S3 = 87.

ELSE

SY = 70. + 3. * LOG(1.E7*STRAIN_RATE)

S1 = SY + 10. * SY / 70.

S2 = SY + 14. * SY / 70.

S3 = SY + 17. * SY / 70.

ENDIF

E1=0.01

E2=0.015

E3=0.2

PVM(1, MN) = SY

PVM(2, MN) = S1

PVM(3, MN) = S2

PVM(4, MN) = S3

PVM(5, MN) = E1

PVM(6, MN) = E2

PVM(7, MN) = E3

!-----------------------------------------------------------------------

! MATERIAL # 3: properties = linear function of temperature

! for use with user constitutive model (actually b-p)

!-----------------------------------------------------------------------

ELSEIF (MN .EQ. 3) THEN

IF (CTEMP .LT. 21.0) CTEMP = 21.0

IF (CTEMP .GT. 400.) CTEMP = 400.

! -- Elastic

E = 72.4E9 - 81.53E6 * (CTEMP - 21.)

FN = 0.33 + 7.916E-5 * (CTEMP - 21.)

ALP = 22.5E-6 + 3.958E-9 * (CTEMP - 21.)

NE = 5

PEM(1, MN) = E

PEM(2, MN) = E

PEM(3, MN) = FN

PEM(4, MN) = FN

PEM(5, MN) = E / (2. * (1. + FN))

ALPA(MN) = ALP

ALPT(MN) = ALP

! -- Viscoplastic (Bodner-Partom)

D0 = 1.E4

Z0 = 340.E6

Z1 = 435.E6

BM = 300.0

AN = 10.0 - 0.02493 * (CTEMP - 21.)

Q = 1.0

NV = 6

PVM(1, MN) = D0

PVM(2, MN) = Z0

PVM(3, MN) = Z1

PVM(4, MN) = BM

PVM(5, MN) = AN

PVM(6, MN) = Q

!-----------------------------------------------------------------------

! MATERIAL # 4: Fiber (NCMD = 6) with local failure = funct of temp

!-----------------------------------------------------------------------

ELSEIF (MN .EQ. 4) THEN

PEM(1, MN) = 58.E3

PEM(2, MN) = 58.E3

PEM(3, MN) = 0.25

PEM(4, MN) = 0.25

PEM(5, MN) = 23.2E3

ALPA(MN) = 3.5E-6

ALPT(MN) = 3.5E-6

! -- Note: *SUBCELL_FAILURE must be specified in the input file to

! enable local failure checking. Any failure properties

! specified here will replace those specified in the input file

XFAILT(MN, 1, 1) = 3500. - 1.8 * (CTEMP - 21.)

!-----------------------------------------------------------------------

! MATERIAL #5: Matrix (NCMD = 6) with damage

!-----------------------------------------------------------------------

ELSEIF (MN .EQ. 5) THEN

PEM(1, MN) = 12770.

PEM(2, MN) = 12770.

PEM(3, MN) = 0.32

PEM(4, MN) = 0.32

PEM(5, MN) = PEM(1, MN)/(2. * (1.+ PEM(3, MN)))

ALPA(MN) = 21.06E-6

ALPT(MN) = 21.06E-6

! -- Note: *DAMAGE must be specified in the input file to enable fatigue

! damage analysis. Any damage properties specified here will

! replace those specified in the input file

ZDAM(MN, 1) = 0.

ZDAM(MN, 2) = 0.

ZDAM(MN, 3) = 0.

ZDAM(MN, 4) = 1.

ZDAM(MN, 5) = 1.

ZDAM(MN, 6) = 1.

ZDAM(MN, 7) = 1.

ZDAM(MN, 8) = 1.

ZDAM(MN, 9) = 1.

ZDAM(MN, 10)= 2.27

ZDAM(MN, 11) = 0

ZDAM(MN, 12) = 0.2302

ZDAM(MN, 13) = 20.3

ZDAM(MN, 14) = 900.

ZDAM(MN, 15) = 128.

NZDAM(MN) = 0

ENDIF

!***********************************************************************

! END USER EDITS *

!***********************************************************************

usrmat.F90: User-defined material constitutive model file

!***********************************************************************

! BEGIN USER EDITS *

!***********************************************************************

! -- Consider placing your own message here to ensure that your code is

! being executed

IF (TIME .EQ. 0.D0) THEN

WRITE(NIO, *) '*** NOTE: Default USRMAT routine being executed ***'

WRITE(*, *) '*** NOTE: Default USRMAT routine being executed ***'

ENDIF

!-----------------------------------------------------------------------

! MATERIAL #1 -- Power Law Creep

!-----------------------------------------------------------------------

IF (MN .EQ. 1) THEN

! -- Creep material properties

CREEPCOEF = PV(1)

POWER = PV(2)

! -- Deviatoric stress [S] in the subcell

TRACE3 = (SA(7) + SA(8) + SA(9)) / 3.

S(1) = SA(7) - TRACE3

S(2) = SA(8) - TRACE3

S(3) = SA(9) - TRACE3

S(4) = SA(10)

S(5) = SA(11)

S(6) = SA(12)

! -- Effective Stress

SEFF = SQRT((SA(7) - SA(8))**2 + (SA(8) - SA(9))**2 + &

(SA(7) - SA(9))**2 + &

+ 6 * (SA(10)**2 + SA(11)**2 + SA(12)**2)) / SQRT(2.)

CREEP_F = CREEPCOEF * SEFF**POWER

IF (SEFF .GT. 0.D0) THEN

COEF = 3 * CREEP_F / (2 * SEFF)

ELSE

COEF = 0.D0

ENDIF

! -- Inelastic strain increments

DSA(13) = COEF * S(1) * TSTEP

DSA(14) = COEF * S(2) * TSTEP

DSA(15) = COEF * S(3) * TSTEP

DSA(16) = COEF * S(4) * TSTEP

DSA(17) = COEF * S(5) * TSTEP

DSA(18) = COEF * S(6) * TSTEP

!-----------------------------------------------------------------------

! MATERIAL #2 --> Bodner-Partom

!-----------------------------------------------------------------------

ELSEIF (MN .EQ. 2) THEN

! -- Copy appropriate viscoplastic material constants

IF( NV .LT. 6 ) THEN

CALL FATALERROR(NIO)

WRITE(NIO, *) ' NOT ENOUGH PV SPACE: NV =', NV

STOP

ENDIF

D0 = PV(1)

Z0 = PV(2)

Z1 = PV(3)

BM = PV(4)

AN = PV(5)

Q = PV(6)

! -- Copy stress from [SA] to [SS]

SS(1) = SA(7)

SS(2) = SA(8)

SS(3) = SA(9)

SS(4) = SA(10)

SS(5) = SA(11)

SS(6) = SA(12)

! -- Compute the deviatoric stress [S] in the subcell

TEMP = (SS(1) + SS(2) + SS(3)) / 3.0

S(1) = SS(1) - TEMP

S(2) = SS(2) - TEMP

S(3) = SS(3) - TEMP

S(4) = SS(4)

S(5) = SS(5)

S(6) = SS(6)

AJ2 = 0.5 * (S(1)**2 + S(2)**2 + S(3)**2) + S(4)**2 + S(5)**2 + &

S(6)**2

SQ3AJ = DSQRT( SS(1)**2 + SS(2)**2 + SS(3)**2 + 2 * (SS(4)**2 + &

SS(5)**2 + SS(6)**2) )

SQ2 = 1.414215

IF (SQ3AJ .EQ. 0.0) THEN

DO I = 1, 6

R(I) = 0

END DO

ELSE

R(1) = SS(1) / SQ3AJ

R(2) = SS(2) / SQ3AJ

R(3) = SS(3) / SQ3AJ

R(4) = SQ2 * SS(4) / SQ3AJ

R(5) = SQ2 * SS(5) / SQ3AJ

R(6) = SQ2 * SS(6) / SQ3AJ

ENDIF

! -- If D0=0 then assume elastic and zero-out [DSA(13-30)] (inelastic

! strain increments and internal variable increments), then return

IF (D0 .EQ. 0) THEN

DO JJ = 13, 30

DSA(JJ) = 0.0

END DO

RETURN

! -- Inelastic

ELSE

ZEF = Z0 + Q * SA(20) + (1 - Q) * (R(1) * SA(21) + R(2) * &

SA(22) + R(3) * SA(23) + R(4) * SA(24) + R(5) &

* SA(25) + R(6) * SA(26))

IF (AJ2 .EQ. 0.0) THEN

AL = 0.0

ELSE

ARG1 = ZEF**2.0 / (3.0 * AJ2)

IF (ARG1 .GT. 1E6) ARG1 = 1E6

CON = .5 * (AN + 1.0) / AN

ARG = CON * (ARG1)**AN

IF (ARG .GT. 50.0) ARG = 50.0

AL = D0 / (DEXP(ARG) * DSQRT(AJ2))

ENDIF

! -- Inelastic strain increments

DSA(13) = AL * S(1) * TSTEP

DSA(14) = AL * S(2) * TSTEP

DSA(15) = AL * S(3) * TSTEP

DSA(16) = 2 * AL * S(4) * TSTEP

DSA(17) = 2 * AL * S(5) * TSTEP

DSA(18) = 2 * AL * S(6) * TSTEP

! -- Plastic work increment

WPD = S(1) * DSA(13) + S(2) * DSA(14) + S(3) * DSA(15) + S(4) * &

DSA(16) + S(5) * DSA(17) + S(6) * DSA(18)

! -- State variable increments

DSA(19) = WPD

Z0M = BM / Z0

ZD = Z0M * (Z1 - ZEF) * WPD

DSA(20) = ZD

DSA(21) = ZD * R(1)

DSA(22) = ZD * R(2)

DSA(23) = ZD * R(3)

DSA(24) = ZD * R(4)

DSA(25) = ZD * R(5)

DSA(26) = ZD * R(6)

ENDIF

!***********************************************************************

! END USER EDITS *

!***********************************************************************

usrformde.F90: User-defined stiffness matrix calculation file

!***********************************************************************

!* BEGIN USER EDITS *

!***********************************************************************

! -- Consider placing your own message here to ensure that your code is

! being executed

IF (TIME .EQ. 0.D0) THEN

WRITE(NIO, *) '*** NOTE: Default USRFORMDE routine being executed ***'

WRITE(NIO, *) ' Material number', MN

WRITE(*, *) '*** NOTE: Default USRFORMDE routine being executed ***'

WRITE(*, *) ' Material number', MN

ENDIF

! -- Obtain material properties from storage

E = PEM(1, MN)

FN = PEM(2, MN)

GA = E / (2. * (1. + FN))

! -- Zero the stiffness matrix

DO I = 1, 6

DO J = 1, 6

DNEW(I, J) = 0

END DO

! -- Determine the stiffness components

GT = 0.5 * E / (1 + FN)

FK = 0.25 * E / (0.5 * (1 - FN) - FN**2)

DNEW(1, 1) = E + 4.0 * FK * FN**2

DNEW(2, 1) = 2.0 * FK * FN

DNEW(3, 1) = 2.0 * FK * FN

DNEW(1, 2) = 2.0 * FK * FN

DNEW(2, 2) = FK + GT

DNEW(3, 2) = FK - GT

DNEW(1, 3) = 2.0 * FK * FN

DNEW(2, 3) = FK - GT

DNEW(3, 3) = FK + GT

DNEW(4, 4) = GT

DNEW(5, 5) = GA

DNEW(6, 6) = GA

!***********************************************************************

! END USER EDITS *

!***********************************************************************

Index

A=, 174, 177, 178

ABD matrix, 96, 107, 235

accuracy, 3, 64, 81, 86, 158, 188, 213, 241, 242, 251

ACTION=, 159, 162, 166, 168, 169, 170, 189, 191

Adams-Bashforth, 148

admissible, 94, 110

ALF1=, 245

ALF2=, 245

ALF3=, 245

ALF4=, 245

ALF5=, 245

ALF6=, 245

all subcells, 37, 136, 137, 138, 144, 145, 156

allowables, 152, 153, 154, 155, 156, 157, 158, 161, 162, 164, 166, 169, 170

ALPA=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222

ALPT=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222

aluminum, 29, 30, 60, 61, 62, 63, 75, 76, 77, 134, 135, 229, 231, 232, 234, 235

ANG=, 13, 92, 93, 99, 100, 104, 125, 126, 129, 143, 165, 173, 174, 177, 206, 230

ANGINC=, 135, 137, 143, 144

angle increment, 134, 137, 144

anisotropic, 7, 127, 220, 241, 247, 248, 249, 250, 251

apparent stiffness, 97, 98

ARCHID=, 7, 9, 10, 13, 23, 24, 65, 67, 68, 70, 72, 73, 75, 76, 78, 79, 80, 82, 83, 86, 87, 92, 93, 99, 100, 104, 105, 111, 112, 115, 116, 120, 121, 125, 126, 129, 135, 136, 143, 148, 149, 153, 154, 158, 159, 165, 173, 174, 175, 185, 189, 190, 195, 196, 200, 201, 203, 206, 207, 214, 215, 221, 223, 230, 239, 240, 243, 245, 246, 247

architecture, 7, 9, 10, 24, 64, 66, 67, 69, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 84, 85, 87, 92, 99, 102, 103, 112, 116, 120, 121, 136, 143, 148, 149, 153, 154, 159, 175, 185, 190, 195, 196, 201, 206, 207, 215, 223, 237, 240, 246, 247, 251

architecture library, 10, 66, 69, 74, 78, 81

AS=, 221, 223, 229, 230

ASCII files, 4, 11, 28, 60, 137, 144, 195, 202, 206, 208

ASP=, 78, 79, 104, 105, 221, 223

ASP1=, 79, 104, 105, 200, 201

ASP2=, 79, 104, 105, 200, 201

aspect ratio, 67, 68, 72, 73, 79, 87, 105, 112, 121, 149, 154, 159, 175, 185, 201, 207, 215, 223

asymmetric, 104, 107, 108, 109, 129, 235

average material, 156, 169, 170

axial stiffness matrix (A), 14

barium titanate, 220, 221, 222, 223, 226, 228, 229, 232, 235

BaTiO₃, 220, 223, 227

BaTiO₃/CoFe₂O₄, 220, 226, 228, 229, 235

BDN=, 185, 186, 189, 191

BDS=, 185, 186, 187, 189, 191

BE=, 174, 177, 178

bending, 14, 96, 101, 104, 107, 127, 129, 132, 143

bending stiffness (D), 14, 96, 127

biaxial, 110, 113, 165

BLOCK=, 174, 176

BN=, 174, 177, 185, 186, 189, 191

Bodner-Partom, 1, 29, 30, 31, 32, 33, 34, 41, 44, 45, 50, 51, 54, 55, 58, 61, 62, 76, 134, 231, 263, 265

boron, 231, 232, 235

BP=, 174, 177

BS=, 185, 186, 187, 189, 191

C11=, 245

C12=, 245

C13=, 245

C14=, 245

C15=, 245

C16=, 245

C22=, 155, 245

C23=, 245

C24=, 245

C25=, 245

C26=, 245

C33=, 155, 245

C34=, 245

C35=, 245

C36=, 245

C44=, 245

C45=, 245

C46=, 245

C55=, 245

C56=, 245

C66=, 245

characterization, 171, 184, 220

circular fiber, 67, 68, 72, 86, 87, 112, 120, 121, 143, 148, 153, 154, 159, 175, 206, 258

class C_6v electromagnetic materials, 220

CMOD=, 7, 8, 9, 13, 18, 19, 23, 24, 28, 29, 30, 32, 35, 36, 38, 41, 42, 43, 44, 45, 46, 50, 51, 55, 56, 60, 61, 62, 65, 67, 70, 72, 75, 76, 78, 79, 82, 83, 86, 87, 92, 93, 99, 100, 104, 105, 111, 112, 115, 116, 120, 121, 125, 126, 129, 130, 135, 136, 143, 148, 149, 153, 154, 158, 159, 165, 166, 173, 175, 185, 189, 190, 195, 196, 200, 201, 206, 207, 214, 215, 216, 217, 221, 222, 223, 229, 230, 231, 237, 238, 239, 243, 244, 245, 246, 247

cobalt ferrite, 220, 221, 223, 227, 229, 230, 231, 232, 235

coefficient of thermal expansion, 9, 11, 28, 117, 228, 241, 247, 248, 251

CoFe₂O₄, 220, 221, 223, 227, 229, 230, 231, 232, 235

Compaq Visual Fortran, 50

compile, 50

COMPR=, 153, 154, 155, 159, 161, 162, 174, 178, 179

concentrations, 89, 153, 158

conductivity, 8, 9, 11

consistency, 198

constant compliant interface (CCI) model, 184, 186, 187

constitutive equation, 28, 110, 219, 220, 227

constitutive model, 2, 3, 9, 28, 29, 30, 31, 32, 34, 35, 37, 38, 39, 40, 41, 44, 45, 46, 48, 50, 55, 56, 58, 59, 60, 61, 64, 72, 134, 197, 213, 214, 216, 217, 218, 220, 223, 237, 247, 262, 265

controlling subcell, 176

convergence, 30, 36, 68, 216, 217, 226, 234

coordinate system, 12, 14, 92, 211, 212, 247

copper, 29, 30, 36, 37, 60, 61, 62, 171

coupling stiffness matrix (B), 14, 104

creep, 55, 57, 58, 59, 202

creep time, 202

cross shaped fiber, 67

cross-ply, 12, 14, 99, 101, 102, 103, 143, 209, 210, 211, 212

Curtin model, 189, 190, 191, 192, 253, 259

cyclic, 148, 150, 152, 171, 176, 187

D=, 79, 82, 83, 189, 190, 191, 221, 222, 223, 229, 230, 238, 239, 240, 243, 245, 246, 247

damage, 3, 64, 89, 152, 153, 158, 162, 171, 172, 173, 176, 178, 179, 180, 263

damage increment, 176, 180

damage parameter, 171, 172, 176, 178

data output, 194

DBCH=, 185, 186, 189

debonding, 77, 89, 152, 184, 186, 187, 188, 189, 191, 193, 197

debonding parameter, 184, 197

DELAY=, 185, 186, 187, 189, 191

design allowables, 153

diagonal array, 79, 201

DINC=, 174, 176

discontinuous, 64, 105, 202, 203, 204, 205

displacement jump, 184

dissipation rate, 138

diverge, 192

DR=, 79, 104, 105, 135, 137, 143, 144, 200, 201

E1=, 61, 262

E11=, 102, 108, 153, 154, 155, 159, 161

E12=, 153, 154, 155, 159, 161

E13=, 153, 154, 155, 159, 161

E2=, 61, 262

E22=, 102, 108, 153, 154, 155, 159, 161

E23=, 153, 154, 155, 159, 161

E33=, 153, 154, 155, 159, 161

EA=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222

EC11=, 155

EC22=, 155

EC33=, 155

effective compliance matrix, 11, 14

effective properties, 6, 7, 9, 10, 11, 12, 14, 21, 155, 194, 226, 237, 240, 241, 242, 243, 246, 247, 251, 256

effective stiffness matrix, 11, 14, 241, 248, 250

EL=, 7, 8, 13, 41, 42, 43, 44, 45, 46, 55, 56, 61, 70, 221, 223, 229, 230, 238, 239, 243, 244, 246, 247

elastic modulus, 8, 241, 251

electric displacement, 219, 225, 227, 228, 234, 235

electric field, 219, 225, 227, 228, 233

electromagnetic, 3, 213, 219, 220, 222, 223, 225, 226, 227, 228, 229, 231, 232, 234

electromagnetic specifier, 223

electromagnetically active, 213

ellipsoidal, 80

EM=, 221, 222, 223, 229, 230, 231, 232

embedded, 64, 92

end of file, 10

ending time, 52

engineering shear strain, 28, 110, 112

EPS=, 135, 137, 143, 144

equivalent plastic strain, 134, 138, 140, 141, 145, 147

ERR=, 35, 36, 43, 47, 51, 52, 148, 149, 214, 215, 216

error tolerance, 148, 149, 216

errors, 19, 36, 47, 52, 60, 87, 148, 149, 216

ES=, 221, 223, 229, 230

ES11=, 221, 222

ES12=, 221, 222

ES26=, 221, 222

ET=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222

ETFL=, 174, 177

ETM=, 174, 177

ETU=, 174, 177

evolving compliant interface (ECI) model, 184, 186, 187, 189, 190, 192

Example Problem Manual, 1, 5, 9

execution, 4, 30, 41, 50, 61, 87, 134, 137, 162, 164, 168, 169, 170, 177, 192, 217

external material database, 28, 60, 63

EXTMAT=, 60, 62

F=, 7, 9, 10, 13, 23, 24, 65, 67, 70, 72, 78, 79, 86, 87, 92, 93, 99, 100, 104, 111, 112, 115, 116, 120, 121, 125, 126, 129, 135, 136, 143, 148, 149, 153, 154, 158, 159, 165, 173, 174, 175, 185, 189, 190, 195, 196, 200, 201, 206, 207, 214, 215, 221, 223, 230

FACE=, 185, 186, 189, 191

failure, 3, 64, 89, 152, 157, 158, 161, 162, 163, 164, 165, 168, 169, 170, 171, 177, 178, 179, 180, 181, 184, 191, 192, 263

failure criteria, 152, 158, 162, 169, 170, 179

failure parameters, 164, 169, 170

failure surface, 165, 168, 170

fatigue, 152, 171, 172, 173, 176, 178, 179, 180, 263

fatigue limit, 171

fiber breakage, 152, 189, 191, 192, 193

fiber material, 28, 198, 203

fiber strength, 189, 193

fiber volume fraction, 9, 11, 23, 65, 67, 68, 69, 73, 74, 77, 78, 81, 85, 89, 90, 91, 92, 97, 98, 102, 103, 114, 123, 124, 125, 128, 139, 140, 141, 142, 143, 146, 147, 148, 151, 153, 165, 170, 171, 195, 203, 204, 205, 206, 237

field variables, 50, 86, 88

first subcell, 137, 138, 145

flag-type keywords, 8, 154, 155, 161, 162, 178, 179

flow law, 134

force resultant, 93, 94, 98, 103, 107, 108, 110, 125, 131, 143, 145, 167, 170, 176, 232, 235

forward Euler, 20, 30, 148

FREQ=, 18, 21, 23, 25, 29, 31, 32, 33, 35, 37, 38, 39, 43, 47, 51, 52, 56, 57, 60, 62, 65, 68, 70, 73, 76, 77, 79, 80, 83, 85, 86, 88, 93, 94, 99, 101, 104, 106, 111, 113, 115, 117, 120, 122, 125, 127, 148, 150, 159, 163, 174, 179, 185, 187, 189, 192, 195, 196, 197, 200, 202, 206, 208, 215, 216, 222, 226, 231, 234

frequency, 21, 201, 202

fringe plots, 88, 194, 200, 202, 203, 206

GA=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222

general loading, 120, 121, 129, 131, 167, 224, 225, 232

general loading option, 120, 121, 129, 131, 167, 224, 225, 232

global equilibrium, 213, 214, 217

graphite, 7, 9, 10, 11, 12, 13, 14, 28, 129, 130, 153, 154, 157, 158, 159, 164, 165, 166, 167, 169, 170, 171, 172, 173, 175, 180, 181, 182, 183, 237, 238, 240, 241, 242, 248, 250, 251, 252, 256

graphite/epoxy, 7, 10, 11, 12, 13, 14, 129, 157, 164, 165, 169, 170, 171, 172, 180, 181, 182, 183, 237, 238, 240, 241, 242, 248, 250, 252

GVIPS, 2, 18, 24, 28, 30, 32, 33, 34, 41, 42, 45, 67, 72, 79, 83, 87, 93, 100, 105, 112, 116, 121, 126, 136, 143, 149, 185, 190, 196, 201, 207, 213, 214, 215, 216, 217, 218

H=, 75, 76, 79, 83, 189, 190, 230, 239, 240, 243, 245, 246, 247

hexagonal pack, 67, 72

HFGMC, 3, 64, 77, 86, 87, 88, 89, 90, 91, 163, 194, 251, 258

homogenization, 64, 237, 241, 242, 243, 248, 250, 251, 252

hybrid, 69, 74, 229, 235, 236

I=, 70, 72

IA=, 189, 192

IB=, 185, 187, 189, 192, 195, 196, 197

IG=, 185, 187, 189, 192, 195, 196, 197

inclined fibers, 237, 240, 241, 242, 247, 248, 250

incremental plasticity model, 35, 36, 37, 41, 46, 47, 49, 50, 52, 53, 64, 134, 214

indices, 142, 186, 187, 191, 192, 197, 198, 219

inelastic power, 138

inelastic strain rate, 138, 139, 141, 150

inelasticity, 64, 158, 235

initial time step, 150

input file, 4, 5, 7, 8, 9, 10, 12, 13, 18, 19, 21, 22, 25, 29, 31, 41, 43, 44, 47, 52, 57, 60, 64, 67, 72, 73, 75, 76, 80, 83, 84, 93, 100, 112, 115, 130, 138, 154, 159, 166, 169, 170, 175, 179, 180, 190, 207, 209, 215, 216, 220, 223, 231, 232, 239, 240, 246, 247, 257, 263

integration, 20, 25, 30, 33, 36, 39, 47, 52, 57, 62, 68, 73, 76, 80, 84, 86, 87, 88, 94, 101, 106, 113, 116, 122, 127, 132, 136, 144, 148, 149, 151, 160, 168, 176, 186, 191, 196, 201, 208, 213, 216, 217, 226, 234

integration points, 86, 87, 88

interface, 28, 65, 70, 71, 72, 73, 77, 88, 89, 184, 186, 187, 189, 191

interface material, 72

internal material database, 19, 23, 24, 29, 31, 32, 35

IP=, 135, 137, 143, 144

ISPX=, 135, 137, 143, 144

ISPY=, 135, 137, 143, 144

ISR=, 135, 137, 143, 144

ISTM=, 148, 149

ISTT=, 148, 149

iteration, 36, 64, 216

ITMAX=, 35, 36, 43, 47, 51, 52, 214, 215, 216

K=, 7, 8, 9, 13

KS=, 221, 223, 229, 230

KS11=, 221, 222

KS22=, 221, 222

ksi, 102, 186, 187, 191, 192

L=, 75, 76, 83, 84, 189, 190, 230, 239, 240, 243, 245, 246, 247

L0=, 189, 191

laminate, 3, 6, 12, 13, 14, 64, 82, 92, 93, 94, 96, 98, 99, 100, 101, 102, 104, 105, 106, 107, 108, 109, 110, 125, 127, 128, 129, 132, 143, 144, 145, 146, 147, 152, 165, 170, 171, 172, 175, 176, 179, 180, 183, 194, 197, 206, 207, 208, 209, 211, 212, 213, 216, 229, 232, 234, 235, 236

laminate analysis, 3, 14, 64, 92, 93, 94, 96, 99, 100, 104, 105, 110, 144, 197, 208, 209, 229, 232

laminate level plot, 94

LAMINATE=, 93, 94, 99, 101, 104, 106, 125, 127, 174, 179, 206, 208, 231, 234

lamination theory, 3, 12, 14, 64, 82, 92, 96, 99, 102, 104, 125, 143, 145, 234

layer, 3, 12, 14, 64, 92, 93, 95, 96, 97, 98, 99, 101, 102, 103, 104, 105, 107, 127, 143, 144, 145, 169, 170, 197, 206, 208, 209, 210, 211, 212, 229, 232, 235

Legendre polynomial, 87, 88

library file, 50, 52, 55

linear elastic, 28, 152, 153, 155, 156

link, 50, 251

LL=, 79

LN=, 185, 186, 189, 191

load block, 176, 178, 179, 180, 181

load magnitude, 165

loading, 1, 3, 6, 10, 12, 14, 18, 19, 20, 21, 23, 24, 25, 26, 33, 35, 39, 57, 64, 65, 70, 78, 84, 92, 93, 94, 96, 101, 105, 107, 110, 111, 112, 113, 114, 115, 116, 117, 120, 121, 122, 123, 125, 126, 129, 131, 132, 134, 136, 137, 143, 149, 150, 152, 158, 161, 163, 164, 165, 167, 170, 171, 176, 179, 180, 197, 200, 202, 203, 206, 209, 214, 217, 218, 220, 224, 225, 228, 229, 232, 234

loading components, 120, 137

loading cycle, 171, 176

loading option, 19, 24, 84, 94, 110, 111, 112, 114, 120, 125, 126, 129, 180, 225

localization, 64

LOP=, 18, 19, 23, 24, 25, 29, 30, 32, 33, 35, 36, 38, 39, 43, 47, 50, 51, 55, 56, 60, 62, 65, 68, 70, 73, 75, 76, 79, 80, 83, 84, 86, 87, 92, 93, 99, 101, 104, 105, 111, 112, 113, 115, 116, 120, 121, 125, 126, 127, 129, 131, 148, 149, 158, 160, 165, 167, 174, 175, 185, 189, 190, 195, 196, 200, 201, 214, 215, 221, 224, 230, 232

LS=, 185, 186, 187, 189, 191

LY=, 13, 92, 99, 100, 104, 125, 126, 129, 130, 143, 144, 165, 166, 173, 174, 175, 206, 207, 230, 232

LYR=, 174

M=, 7, 8, 9, 10, 13, 18, 19, 23, 24, 29, 30, 32, 33, 35, 36, 38, 41, 42, 43, 44, 45, 46, 47, 50, 51, 55, 56, 60, 62, 65, 67, 70, 72, 75, 78, 79, 82, 86, 87, 92, 93, 99, 100, 104, 111, 112, 115, 116, 120, 121, 125, 126, 129, 135, 136, 143, 148, 149, 153, 154, 158, 159, 165, 173, 174, 175, 185, 189, 190, 191, 195, 196, 200, 201, 206, 207, 214, 215, 221, 222, 223, 229, 230, 238, 239, 243, 244

MACPOST, 194, 200, 202, 203, 204, 205, 253

MAG=, 18, 19, 23, 24, 25, 29, 30, 32, 33, 35, 36, 38, 39, 43, 47, 51, 55, 56, 60, 62, 65, 68, 70, 73, 75, 76, 79, 80, 83, 84, 86, 87, 92, 93, 99, 101, 104, 105, 111, 112, 115, 116, 120, 121, 122, 125, 126, 129, 130, 131, 148, 149, 158, 160, 165, 166, 167, 168, 174, 175, 185, 186, 189, 190, 195, 196, 200, 201, 214, 215, 221, 224, 225, 230, 231, 232, 233, 234

magnetic field, 219, 225, 227, 228, 229, 233, 234, 235, 236

magnetic flux density, 219, 225, 227, 228, 234

magnetic permeability, 219, 220, 223

magnetically asymmetric, 232, 235, 236

magnetoelectric, 219, 220, 223, 227

MAT=, 60, 61, 153, 154, 159, 161, 162, 166, 168, 174, 177, 178

MATDB=, 7, 8, 13, 41, 42, 43, 44, 45, 46, 50, 51, 55, 56, 60, 62, 70, 72, 129, 130, 153, 154, 158, 159, 165, 166, 173, 175, 221, 222, 223, 229, 230, 231, 238, 239, 243, 244, 246, 247

material number, 41, 48, 50, 76, 84, 208, 261

material point, 120, 122

material properties, 7, 8, 9, 13, 18, 19, 20, 21, 23, 24, 28, 41, 44, 45, 46, 48, 50, 54, 55, 60, 70, 72, 97, 132, 223, 231, 240, 247, 248, 257, 265, 268

material property database, 9, 18

MATID=, 7, 8, 13, 18, 19, 23, 24, 29, 30, 32, 33, 35, 36, 38, 41, 42, 43, 44, 45, 46, 50, 51, 55, 56, 60, 62, 65, 67, 70, 72, 75, 76, 78, 79, 82, 83, 86, 87, 92, 93, 99, 100, 104, 105, 111, 112, 115, 116, 120, 121, 125, 126, 129, 130, 135, 136, 143, 148, 149, 153, 154, 158, 159, 165, 166, 173, 175, 185, 189, 190, 195, 196, 200, 201, 206, 207, 214, 215, 221, 222, 223, 229, 230, 231, 238, 239, 243, 244, 246, 247

MATLAB, 1, 4, 86, 88, 194, 206, 208, 209, 211, 212, 259

matrix material, 6, 28, 145, 156, 237, 240, 242, 246, 248, 251

maximum strain, 162

maximum stress, 162, 163, 169, 171

MAXNB=, 174, 176

mean stress, 171

mechanical loading, 3, 10, 18, 19, 24, 25, 33, 38, 39, 50, 55, 57, 65, 94, 110, 111, 112, 114, 115, 116, 117, 120, 122, 125, 129, 132, 134, 136, 137, 148, 149, 150, 153, 158, 161, 164, 170, 176, 202, 203

METHOD=, 18, 20, 23, 25, 29, 30, 32, 33, 35, 36, 38, 39, 43, 47, 51, 52, 55, 57, 60, 62, 65, 68, 70, 73, 75, 76, 79, 80, 83, 84, 86, 87, 92, 94, 99, 101, 104, 106, 111, 113, 115, 116, 120, 122, 125, 127, 130, 132, 135, 136, 148, 149, 159, 160, 166, 168, 174, 176, 185, 186, 189, 191, 195, 196, 200, 201, 206, 208, 214, 215, 216, 222, 226, 231, 234

micro level plot, 21

micromechanics, 3, 28, 64, 118, 164, 198, 219

midplane curvature, 94, 109, 125

midplane strain, 92, 94, 96, 98, 99, 101, 103, 104, 105, 107, 108, 109, 110, 125, 126, 127, 128, 129, 235

minimal output, 31

minimum time step, 149

MINSTEP=, 148, 149

mission profile, 122

MMAX=, 135, 136, 143, 144

MOD=, 7, 9, 13, 18, 19, 23, 24, 29, 30, 32, 33, 35, 36, 38, 43, 47, 50, 51, 55, 56, 60, 62, 64, 65, 67, 70, 72, 75, 76, 78, 79, 82, 83, 86, 87, 92, 93, 99, 100, 104, 111, 112, 115, 116, 120, 121, 125, 126, 129, 135, 136, 143, 148, 149, 153, 154, 158, 159, 165, 173, 174, 175, 177, 185, 189, 190, 195, 196, 200, 201, 206, 207, 214, 215, 221, 223, 230, 239, 240, 243, 245, 246, 247

mode, 19, 24, 30, 33, 36, 39, 47, 51, 57, 62, 68, 73, 76, 80, 84, 87, 94, 101, 105, 112, 116, 122, 126, 136, 137, 144, 160, 175, 186, 190, 196, 201, 215

MODE=, 18, 19, 23, 24, 25, 29, 30, 32, 33, 35, 36, 38, 39, 43, 47, 51, 55, 56, 57, 60, 62, 65, 68, 70, 73, 75, 76, 79, 80, 83, 84, 86, 87, 92, 94, 99, 101, 104, 105, 111, 112, 115, 116, 120, 121, 122, 125, 126, 129, 130, 131, 135, 136, 143, 144, 148, 149, 158, 160, 165, 166, 167, 168, 174, 175, 185, 186, 189, 190, 195, 196, 200, 201, 214, 215, 221, 224, 225, 230, 231, 232, 233, 234

modified Bodner-Partom, 32, 33, 34

moment resultant, 14, 94, 96, 107, 109, 110, 125, 129, 131, 132, 167, 168, 233, 235

monoclinic, 241, 242, 247, 248, 250

monolithic, 6, 18, 19, 29, 30, 33, 36, 64, 105, 134, 228

monolithic material, 19, 21, 30, 33, 35, 36, 50, 64

MPa, 56, 132, 154, 155, 161, 162, 163, 164, 167, 168, 169, 170, 171, 175, 176, 177, 178

MS=, 221, 223, 229, 230

MS11=, 221, 222

MS22=, 221, 222

multimechanism, 213, 214, 217, 218

multi-scale, 92

N=, 86, 88, 206, 208

N1=, 174, 177

N2=, 174, 177

NAI=, 189, 191

NAME=, 18, 21, 23, 25, 29, 31, 32, 34, 35, 37, 38, 39, 43, 47, 51, 52, 56, 57, 60, 61, 62, 65, 68, 70, 73, 76, 77, 79, 80, 83, 85, 86, 88, 93, 94, 99, 101, 104, 106, 111, 113, 115, 117, 120, 123, 125, 127, 148, 150, 159, 163, 174, 179, 185, 187, 189, 192, 195, 196, 197, 200, 202, 206, 208, 209, 215, 216, 222, 226, 231, 234

NASA, 3, 253, 254, 256

NBI=, 185, 186, 189, 191

NDMAT=, 174, 177

NGI=, 185, 186, 189, 191

NII=, 185, 186, 189, 191

NINTEG=, 86, 87, 88

NiTi, 38, 39, 40

NLEG=, 86, 87, 88

NLY=, 13, 92, 93, 99, 100, 104, 105, 125, 126, 129, 130, 143, 144, 165, 166, 173, 175, 206, 207, 230, 231

NMAT=, 153, 154, 159, 161, 166, 168, 174, 178

NMATS=, 7, 8, 13, 18, 23, 29, 30, 32, 35, 36, 38, 41, 43, 50, 51, 55, 56, 60, 62, 65, 67, 70, 72, 75, 76, 78, 79, 82, 83, 86, 87, 92, 93, 99, 100, 104, 105, 111, 112, 115, 120, 121, 125, 126, 129, 130, 135, 143, 148, 153, 154, 158, 159, 165, 166, 173, 175, 184, 185, 189, 190, 195, 200, 201, 206, 207, 214, 215, 220, 222, 229, 231, 238, 239, 243, 244, 245, 246

NonLinear Cumulative Damage Rule, 171

NP=, 42, 43, 45, 46

NPL=, 7, 10, 13, 14, 18, 20, 23, 25, 29, 31, 32, 33, 35, 37, 38, 39, 43, 47, 51, 52, 55, 57, 60, 62, 65, 68, 70, 73, 76, 77, 79, 80, 83, 84, 86, 88, 92, 94, 96, 99, 101, 104, 106, 111, 113, 115, 117, 120, 122, 125, 127, 130, 132, 135, 138, 143, 145, 148, 150, 154, 155, 159, 162, 166, 169, 174, 179, 185, 187, 189, 192, 195, 196, 200, 201, 206, 208, 215, 216, 222, 226, 231, 234, 239, 240, 244, 245, 246, 247

NPT=, 18, 19, 20, 23, 24, 25, 29, 30, 32, 33, 35, 36, 38, 39, 43, 47, 51, 52, 55, 56, 57, 60, 62, 65, 68, 70, 73, 75, 76, 79, 80, 83, 84, 86, 87, 92, 93, 94, 99, 101, 104, 105, 106, 111, 112, 113, 115, 116, 117, 120, 121, 122, 125, 126, 127, 129, 130, 131, 132, 135, 136, 148, 149, 158, 159, 160, 165, 166, 167, 168, 174, 175, 176, 185, 186, 189, 190, 191, 195, 196, 200, 201, 206, 207, 208, 214, 215, 216, 221, 222, 224, 225, 226, 230, 231, 232, 233, 234

NPV=, 55, 56, 61

NTEMP=, 7, 8

NTP=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222, 244

NUA=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222

number of subcells, 87

NUT=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222

OMFL=, 174, 177

OMM=, 174, 177

OMU=, 174, 177

ONERA, 171

open cell, 80

OPT=, 79

OPTION=, 135, 136, 143, 144

order, 9, 35, 39, 41, 44, 45, 46, 50, 55, 84, 86, 88, 93, 100, 112, 134, 137, 148, 149, 161, 169, 170, 186, 187, 191, 192, 200, 202, 206, 207, 213, 214, 216, 240, 241, 242, 246, 251

orthotropic, 123, 241, 247, 248, 250

out-of-plane, 7, 64, 85, 92, 96, 235

output, 2, 3, 10, 11, 14, 21, 31, 36, 88, 94, 95, 96, 97, 102, 108, 117, 132, 137, 138, 155, 162, 163, 170, 179, 192, 194, 201, 202, 208, 211, 212, 226, 227, 228, 235, 241, 255, 256

output file, 2, 10, 11, 14, 21, 31, 36, 95, 96, 97, 102, 108, 117, 132, 137, 138, 155, 162, 163, 170, 179, 192, 194, 202, 208, 226, 228, 235, 241, 255, 256

packing, 67, 68, 73, 80

particulate, 64, 105, 220, 226

PATRAN, 1, 4, 194, 200, 201, 202, 203, 204, 205, 259

PELS=, 221, 223, 229, 230

PELS1=, 221, 222

PELS2=, 221, 222

perfectly bonded, 187, 188

piezoelectric, 219, 220, 223, 227

piezomagnetic, 219, 220, 223, 227, 235

plain weave, 237, 238, 240, 241, 242, 243, 244, 247, 248, 250, 252

plane of transverse isotropy, 223

ply, 3, 12, 14, 64, 92, 93, 95, 96, 97, 98, 99, 101, 102, 103, 104, 105, 107, 127, 143, 144, 145, 169, 170, 197, 206, 208, 209, 210, 211, 212, 229, 232, 235

PMGS=, 221, 223, 229, 230

PMGS1=, 221, 222

PMGS2=, 221, 222

Poisson effect, 26, 96

Poisson ratio, 8, 97, 251

poling direction, 220, 223, 229, 230, 235

post-processing, 194, 200, 206

power law creep, 55, 58

preload, 137

preloading, 136, 137, 144, 201, 202

principal material coordinates, 96, 97

print level, 10, 14, 20, 21, 25, 30, 31, 33, 37, 39, 47, 52, 57, 62, 68, 73, 77, 80, 84, 88, 94, 96, 101, 106, 113, 117, 122, 127, 132, 138, 145, 150, 155, 162, 169, 179, 187, 192, 194, 196, 201, 208, 216, 226, 234, 240, 246, 247

probing, 134, 136, 137, 144

pyroelectric, 219, 220, 223

pyromagnetic, 219, 220, 223, 228

QS=, 221, 223, 229, 230

QS11=, 221, 222

QS12=, 221, 222

QS26=, 221, 222

quasi-isotropic, 99, 101, 102, 103, 125, 127, 128, 165, 170, 171, 175, 180, 183

R=, 65, 67, 68, 70, 72, 86, 87, 99, 100, 104, 111, 112, 120, 121, 125, 126, 129, 143, 148, 149, 153, 154, 158, 159, 165, 173, 174, 175, 185, 206, 207, 214, 215

RA=, 79

RAD=, 70, 72

RAD1=, 65, 67, 70, 72

RAD2=, 65, 67, 70, 72

RC=, 79

rectangular pack, 67, 68, 72, 87, 100, 105, 112, 121, 126, 130, 144, 149, 154, 159, 166, 167, 175, 185, 207

redistribution, 177, 180

reduced stiffness matrices (Q), 96

reference temperature, 19, 219

REFTIME=, 115, 116, 148, 149, 158, 160, 185, 189, 190, 200, 201, 214, 215

repeating unit cell analysis, 1, 9, 12, 14, 19, 64, 93, 94, 96, 110, 111, 120, 125, 137, 197, 208, 209, 220

repeating unit cell dimensions, 79

repeating unit cell failure, 170

residual stress, 115, 118, 119, 136, 138, 139, 140, 141, 145, 153, 158, 163, 164, 176, 188, 192, 211

residual stresses, 115, 116, 118, 119, 136, 138, 139, 140, 141, 145, 148, 153, 158, 160, 161, 163, 164, 176, 188, 192, 203, 206, 209, 211, 212

results, 3, 5, 9, 10, 11, 14, 21, 22, 23, 26, 31, 34, 35, 37, 41, 47, 48, 52, 58, 63, 68, 77, 86, 88, 89, 102, 107, 108, 113, 115, 116, 117, 119, 123, 125, 126, 132, 137, 138, 149, 152, 156, 163, 168, 169, 170, 179, 187, 190, 192, 194, 215, 216, 226, 232, 237, 240, 241, 242, 250, 256

reversal tolerance, 186, 187, 191

RITFR=, 70

RITFR1=, 70

RITFR2=, 70

Runge-Kutta, 148, 149

S11=, 153, 154, 159, 161

S12=, 153, 154, 155, 159, 161

S13=, 153, 154, 155, 159, 161

S22=, 153, 154, 159, 161

S23=, 153, 154, 155, 159, 161

S33=, 153, 154, 155, 159, 161

SC11=, 155

SC22=, 155

SC33=, 155

scatter, 194

SCS-6, 60, 61, 62, 125

self-adaptive, 20, 148

SFL=, 174, 177, 178

shape memory alloy, 1, 38, 39, 40

shear coupling, 77, 86, 88, 101, 127

shear CTEs, 227, 241, 248, 249, 250, 252

shear modulus, 8, 97, 102, 251

short fiber, 79, 80, 105, 200, 201, 223, 232

SiC, 1, 23, 24, 26, 27, 28, 67, 68, 69, 72, 73, 74, 79, 81, 83, 85, 86, 87, 89, 90, 91, 92, 93, 96, 97, 98, 99, 100, 102, 103, 104, 105, 108, 109, 112, 114, 115, 116, 117, 118, 119, 120, 121, 123, 124, 125, 126, 128, 135, 136, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 184, 185, 188, 190, 193, 195, 196, 197, 199, 200, 201, 202, 203, 204, 205, 206, 207, 210, 211, 212, 214, 215, 216, 217, 218

SiC/Ti-21S, 1, 23, 26, 27, 68, 69, 74, 81, 85, 89, 90, 91, 92, 96, 97, 98, 99, 102, 103, 104, 105, 108, 109, 114, 115, 117, 118, 119, 123, 124, 128, 139, 140, 141, 142, 143, 145, 146, 147, 150, 151, 184, 188, 193, 197, 199, 202, 203, 204, 205, 210, 211, 212, 214, 216, 217, 218

SIG0=, 189, 191

SM=, 75, 76, 83, 84, 189, 190, 230, 239, 240, 243, 244, 245, 246, 247

smart, 3, 213, 220, 226, 227, 228, 229, 235, 236

S-N curve, 171, 176, 180, 181, 182, 183

source, 8, 13, 43, 50, 51, 52, 56, 62, 130, 154, 159, 166, 175, 194, 206, 208, 223, 231, 239, 246, 247

special case, 10, 35, 46, 67, 73

square array, 79, 223, 232

square diagonal pack, 67, 72

square fiber, 9, 13, 14, 24, 67, 68, 72, 92, 93, 116, 190, 195, 196

square pack, 9, 13, 14, 24, 67, 72, 87, 92, 93, 116, 121, 136, 149, 154, 159, 175, 190, 195, 196, 207, 215

state variables, 197

static failure, 152, 158, 161, 162, 164, 165, 168, 169, 170, 178, 179

step size, 20, 25, 30, 33, 36, 37, 39, 47, 52, 57, 62, 68, 73, 77, 80, 84, 87, 94, 101, 106, 113, 117, 122, 127, 132, 136, 137, 144, 148, 149, 160, 161, 168, 176, 186, 191, 196, 201, 208, 214, 216, 217, 218, 226, 234

stiffness matrix, 2, 11, 14, 21, 28, 55, 104, 110, 213, 219, 241, 247, 248, 249, 250, 251, 268

stiffness reduction, 172, 178

stop execution, 192

STP=, 18, 20, 23, 25, 29, 30, 32, 33, 35, 36, 38, 39, 43, 47, 51, 52, 55, 57, 60, 62, 65, 68, 70, 73, 75, 77, 79, 80, 83, 84, 86, 87, 92, 94, 99, 101, 104, 106, 111, 113, 115, 117, 120, 122, 125, 127, 130, 132, 135, 136, 143, 144, 159, 160, 166, 168, 174, 176, 185, 186, 189, 191, 195, 196, 200, 201, 206, 208, 214, 215, 216, 222, 226, 231, 234

strain allowables, 153, 154, 155, 156, 157, 161

strain rate, 20, 22, 32, 33, 34, 35, 50, 51, 53, 58, 137, 144, 261

strain reference time, 116, 149, 185, 190, 201, 215

stress allowables, 154, 156, 157, 161

stress resultant, 93, 107, 108, 110, 131, 143, 145, 232, 235

stress-strain curve, 34, 35, 39, 52, 63, 115, 118, 194, 199, 216, 217

stress-strain curves, 21, 22, 25, 26, 29, 31, 34, 35, 37, 39, 40, 46, 48, 49, 52, 53, 54, 57, 58, 63, 69, 74, 77, 81, 85, 89, 96, 98, 103, 114, 115, 116, 118, 137, 150, 163, 181, 188, 192, 193, 194, 199, 202, 203, 216, 217

SU=, 174, 177, 178

SU1=, 174, 177

SU2=, 174, 177

subcell failure, 158, 162, 163, 164, 169, 170, 192

surf_1st.dat, 137, 145

surf_1st_ply.dat, 144

surf_all.dat, 137, 145

surf_all_plies.dat, 144

surf_global.dat, 137, 144

surf_local.dat, 137, 145

surf_plies.dat, 144

TAU0=, 189, 191

TEM=, 41, 42, 43, 44, 45, 46, 61, 129, 153, 158, 165, 173, 221, 222, 245

TEMP=, 7, 8, 23, 24, 25, 43, 47, 51, 52, 55, 57, 60, 62, 65, 68, 70, 73, 79, 80, 83, 84, 86, 87, 92, 94, 99, 101, 104, 105, 111, 113, 115, 116, 120, 122, 125, 127, 130, 132, 135, 136, 148, 149, 158, 160, 166, 168, 174, 176, 185, 186, 189, 191, 195, 196, 200, 201, 206, 207, 214, 216, 221, 226, 231, 234

temperature, 7, 8, 9, 19, 20, 21, 24, 25, 26, 27, 28, 29, 31, 32, 35, 37, 41, 44, 46, 48, 50, 51, 52, 54, 92, 116, 117, 118, 122, 123, 129, 132, 135, 136, 137, 144, 150, 151, 164, 170, 176, 181, 182, 186, 191, 202, 208, 209, 216, 217, 218, 219, 223, 228, 247, 248, 262

temperature unit, 19

temperature-dependent, 8, 9, 41, 44, 46, 48, 129, 132, 223, 247

temperature-independent, 7, 8, 41, 44, 48, 223

tensorial shear strains, 112

Theory Manual, 3, 5, 14, 64, 86, 87, 92, 99, 104, 134, 148, 149, 162, 171, 178, 184, 187, 216

thermal loading, 6, 19, 20, 21, 23, 24, 25, 26, 116, 122, 136, 176, 209, 228

thermal strain, 28, 96, 110, 117, 152, 198, 202, 219

THK=, 13, 92, 93, 99, 100, 104, 125, 126, 129, 143, 165, 173, 174, 206, 230

through-thickness, 64, 125, 209, 229, 235, 236, 242, 245, 248, 251

TI=, 18, 19, 20, 23, 24, 25, 29, 30, 32, 33, 35, 36, 38, 39, 43, 47, 51, 52, 55, 56, 57, 60, 62, 65, 68, 70, 73, 75, 76, 77, 79, 80, 83, 84, 86, 87, 92, 93, 94, 99, 101, 104, 105, 106, 111, 112, 113, 115, 116, 117, 120, 121, 122, 125, 126, 127, 129, 130, 131, 132, 135, 136, 148, 149, 158, 159, 160, 165, 166, 167, 168, 174, 175, 176, 185, 186, 189, 190, 191, 195, 196, 200, 201, 206, 207, 208, 214, 215, 216, 221, 222, 224, 225, 226, 230, 231, 232, 233, 234

Ti-15-3, 35, 36, 37

Ti-21S, 1, 18, 19, 21, 22, 23, 24, 26, 27, 28, 32, 33, 34, 67, 68, 69, 72, 74, 79, 81, 83, 85, 86, 87, 89, 90, 91, 92, 93, 96, 97, 98, 99, 100, 102, 103, 104, 105, 108, 109, 112, 114, 115, 116, 117, 118, 119, 120, 121, 123, 124, 125, 126, 128, 136, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 184, 185, 188, 190, 193, 195, 196, 197, 199, 200, 201, 202, 203, 204, 205, 206, 207, 210, 211, 212, 214, 215, 216, 217, 218

Ti-24-11, 35, 36, 37

time delay, 186, 187, 191, 192

time integration, 20, 30, 148, 149, 151, 216

time-based output, 96, 228

TIMES=, 86, 88, 206, 208

titanium, 1, 18, 19, 21, 22, 23, 24, 26, 27, 28, 29, 30, 32, 33, 34, 35, 36, 37, 67, 68, 69, 72, 74, 79, 81, 83, 85, 86, 87, 89, 90, 91, 92, 93, 96, 97, 98, 99, 100, 102, 103, 104, 105, 108, 109, 112, 114, 115, 116, 117, 118, 119, 120, 121, 123, 124, 125, 126, 128, 136, 139, 140, 141, 142, 143, 144, 145, 146, 147, 148, 149, 150, 151, 184, 185, 188, 190, 193, 195, 196, 197, 199, 200, 201, 202, 203, 204, 205, 206, 207, 210, 211, 212, 214, 215, 216, 217, 218

TMAX=, 135, 136, 143, 144

TOLN=, 185, 186, 187, 189, 191

tows, 237

TPRE=, 200, 201

transversely isotropic, 9, 171, 220, 222, 223, 231, 237, 239, 240, 245

TREF=, 18, 19, 29, 30, 32, 33, 35, 36, 38, 75, 76, 135, 136, 143, 144

Tsai-Hill, 162, 168, 169

ultimate strength, 171

unconditionally stable, 213, 214

units, 9, 19, 133, 228

unloading, 39, 150

user-defined, 8, 9, 13, 28, 41, 44, 45, 46, 48, 49, 50, 55, 56, 58, 59, 72, 75, 76, 77, 82, 84, 85, 129

usrformde, 2, 55, 58, 63, 255, 268

usrfun, 2, 9, 50, 51, 52, 255, 261

usrmat, 2, 55, 58, 63, 255, 265

V1=, 42, 43, 44, 45, 46, 61

V2=, 42, 43, 44, 45, 46, 61

VF=, 7, 9, 10, 13, 23, 24, 65, 67, 70, 72, 78, 79, 86, 87, 92, 99, 100, 104, 111, 112, 115, 116, 120, 121, 125, 126, 129, 135, 136, 143, 148, 149, 153, 154, 158, 159, 165, 173, 174, 175, 185, 189, 190, 195, 196, 200, 201, 206, 207, 214, 215, 221, 223, 230

VF1=, 65, 67, 70, 72

VI=, 41, 42, 44, 45, 46, 55, 56, 61, 70, 230

volume fraction, 9, 11, 23, 24, 65, 67, 68, 69, 72, 73, 74, 77, 78, 79, 81, 85, 87, 89, 90, 91, 97, 98, 102, 103, 112, 114, 116, 121, 123, 124, 125, 128, 136, 139, 140, 141, 142, 145, 146, 147, 149, 151, 154, 159, 165, 170, 171, 175, 185, 190, 196, 200, 201, 203, 204, 205, 207, 215, 223, 237

warnings, 21

Weibull modulus, 191

Windows, 50

woven composite, 213, 237, 240, 241, 242, 250, 251

X=, 18, 21, 23, 25, 29, 31, 32, 34, 35, 37, 38, 39, 43, 47, 51, 52, 56, 57, 60, 62, 65, 68, 70, 73, 76, 77, 79, 80, 83, 85, 86, 88, 93, 94, 99, 101, 104, 106, 111, 113, 115, 117, 120, 123, 125, 127, 148, 150, 159, 163, 174, 179, 185, 187, 189, 192, 195, 196, 197, 200, 202, 206, 208, 209, 215, 216, 222, 226, 231, 235

X11=, 159, 161, 162, 166, 168, 169, 174, 178

X12=, 159, 162, 166, 168, 169, 174, 178, 179

X13=, 159, 162, 166, 168, 169, 174, 178, 179

X22=, 159, 161, 162, 166, 168, 169, 174, 178

X23=, 159, 161, 162, 166, 168, 169, 174, 178

X33=, 159, 161, 162, 166, 168, 169, 174, 178

XA=, 65, 67

XML=, 174, 177, 178

x-y plot, 10, 14, 21, 25, 31, 33, 37, 39, 47, 52, 57, 62, 68, 73, 77, 80, 85, 88, 94, 101, 106, 113, 117, 122, 127, 132, 137, 138, 145, 150, 155, 163, 169, 179, 180, 187, 192, 195, 196, 197, 198, 200, 202, 208, 209, 216, 226, 234, 240, 246, 247

Y=, 18, 21, 23, 25, 29, 31, 32, 34, 35, 37, 38, 39, 43, 47, 51, 52, 56, 57, 60, 62, 65, 68, 70, 73, 76, 77, 79, 80, 83, 85, 86, 88, 93, 94, 99, 101, 104, 106, 111, 113, 115, 117, 120, 123, 125, 127, 148, 150, 159, 163, 174, 179, 185, 187, 189, 192, 195, 196, 197, 200, 202, 206, 208, 209, 215, 216, 222, 226, 231, 235

yield criteria, 134, 137

yield surface, 35, 46, 50, 53, 58, 88, 101, 134, 135, 136, 137, 138, 139, 140, 141, 143, 144, 145, 146, 147, 150, 165, 203, 242

zero stiffness, 171